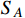Abstract
The XENON1T excess of keV electron recoil events may be induced by the scattering of electrons and long-lived particles with an MeV mass and high speed. We consider a tangible model composed of two scalar MeV dark matter (DM) particles, 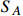 and
and 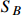 , to interpret the XENON1T keV excess via boosted
, to interpret the XENON1T keV excess via boosted 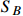 . A small mass splitting
. A small mass splitting 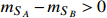 is introduced, and the boosted
is introduced, and the boosted 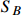 can be produced using the dark annihilation process of
can be produced using the dark annihilation process of 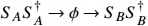 via a resonant scalar ϕ.
via a resonant scalar ϕ.  electron scattering is intermediated by a vector boson X. Although the constraints from Big Bang nucleosynthesis, cosmic microwave background (CMB), and low-energy experiments set the
electron scattering is intermediated by a vector boson X. Although the constraints from Big Bang nucleosynthesis, cosmic microwave background (CMB), and low-energy experiments set the 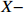 mediated
mediated 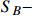 electron scattering cross section to be
electron scattering cross section to be 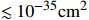 , the MeV scale DM with a resonance enhanced dark annihilation today can still provide sufficient boosted
, the MeV scale DM with a resonance enhanced dark annihilation today can still provide sufficient boosted  and induce the XENON1T keV excess. The relic density of
and induce the XENON1T keV excess. The relic density of  is significantly reduced by the s-wave process
is significantly reduced by the s-wave process 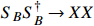 , which is permitted by the constraints from CMB and 21-cm absorption. A very small relic fraction of
, which is permitted by the constraints from CMB and 21-cm absorption. A very small relic fraction of 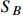 is compatible with the stringent bounds on un-boosted
is compatible with the stringent bounds on un-boosted 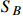 -electron scattering in DM direct detection, and the
-electron scattering in DM direct detection, and the 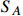 -electron scattering is also allowed.
-electron scattering is also allowed.
Content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI. Article funded by SCOAP and published under licence by Chinese Physical Society and the Institute of High Energy Physics of the Chinese Academy of Sciences and the Institute of Modern Physics of the Chinese Academy of Sciences and IOP Publishing Ltd
I. INTRODUCTION
The existence of dark matter (DM) has been established through extensive cosmological and astronomical observations. However, the microscopic properties of DM beyond the Standard Model (SM) are largely unknown. Recently, the XENON collaboration reported an excess of electronic recoil events with an energy of approximately 2–3 keV [1], and the event distribution has a broad spectrum for the excess. They collected low-energy electron recoil data from the XENON1T experiment with an exposure of 0.65 tonne-years and analyzed various backgrounds for the excess events. Although a small tritium background fits the excess data well [1], bosonic DM can also provide a plausible source for the peak-like excess.
The excess of electron recoil events may be induced by new long-lived particle scattering with electrons in a detector. The lifetime of the new particle must be sufficiently long to reach a detector on Earth after its production and it has an appreciable interaction with electrons. The mass of the new long-lived particle should be
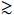 MeV and the velocity should at the level of
MeV and the velocity should at the level of
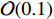 c [2]. Meanwhile, it should be compatible with the structure formation of the universe and the constraints from Big Bang nucleosynthesis (BBN) as well as the cosmic microwave background (CMB). Thus, an exotic mechanism is required to produce many long-lived particles with a high speed. A plausible scenario for the electron excess events is boosted DM produced in the present universe via dark sector annihilation or decay [2–9]. Meanwhile, a fraction of the un-boosted DM with a regular velocity distribution (with a velocity of
c [2]. Meanwhile, it should be compatible with the structure formation of the universe and the constraints from Big Bang nucleosynthesis (BBN) as well as the cosmic microwave background (CMB). Thus, an exotic mechanism is required to produce many long-lived particles with a high speed. A plausible scenario for the electron excess events is boosted DM produced in the present universe via dark sector annihilation or decay [2–9]. Meanwhile, a fraction of the un-boosted DM with a regular velocity distribution (with a velocity of
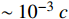 in the galaxy) can also be present today and is detectable via the scattering off electron. Thus, the direct detection experiments would set stringent bounds on the un-boosted DM-electron scattering for the recoil energy of a few eV [10–14]. These bounds must be evaded when interpreting the XENON1T keV excess.
in the galaxy) can also be present today and is detectable via the scattering off electron. Thus, the direct detection experiments would set stringent bounds on the un-boosted DM-electron scattering for the recoil energy of a few eV [10–14]. These bounds must be evaded when interpreting the XENON1T keV excess.
In the interpretation of the XENON1T excess via the scattering between electron and boosted DM, the nature of the intermediating particle and interaction becomes a key aspect. For a long-lived light mediator with keV
 MeV mass, BBN and CMB would place stringent constraints [15, 16]. If the new mediator has a short lifetime, because of the constraint from BBN, its mass should be
MeV mass, BBN and CMB would place stringent constraints [15, 16]. If the new mediator has a short lifetime, because of the constraint from BBN, its mass should be
 10 MeV, and its lifetime is much shorter than a second [17–20]. In addition, the constraints from low-energy experiments, such as NA48/2 [21] and NA64 [22], should be considered. However, the new mediator and interaction may leave some traces in anomalous processes; for example, a new vector boson of about 17 MeV [23, 24], predominantly decaying into
10 MeV, and its lifetime is much shorter than a second [17–20]. In addition, the constraints from low-energy experiments, such as NA48/2 [21] and NA64 [22], should be considered. However, the new mediator and interaction may leave some traces in anomalous processes; for example, a new vector boson of about 17 MeV [23, 24], predominantly decaying into
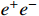 , was suggested by two anomalous transitions of 8Be [25] and 4He [26]. Here, we consider a light vector boson X in general, which primarily decays into
, was suggested by two anomalous transitions of 8Be [25] and 4He [26]. Here, we consider a light vector boson X in general, which primarily decays into
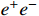 and intermediates the scattering between electron and the boosted DM. Considering the constraints from low-energy experiments [21, 22], when
and intermediates the scattering between electron and the boosted DM. Considering the constraints from low-energy experiments [21, 22], when
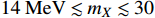 MeV, as shown in Fig. 5 of Ref. [22], a part of the parameter
MeV, as shown in Fig. 5 of Ref. [22], a part of the parameter
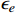 (the
(the
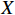 -electron coupling is parameterized as
-electron coupling is parameterized as
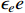 ) in the range of
) in the range of
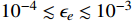 is still permitted by the experiments. Note that the rapid fluctuations in the NA48/2 limit [21] cause some uncertainty of the NA48/2 limit. Here we take the NA48/2 limit in a smooth way as shown in Fig. 5 of Ref. [22] instead of the rapid fluctuations. For instance, the range of
is still permitted by the experiments. Note that the rapid fluctuations in the NA48/2 limit [21] cause some uncertainty of the NA48/2 limit. Here we take the NA48/2 limit in a smooth way as shown in Fig. 5 of Ref. [22] instead of the rapid fluctuations. For instance, the range of
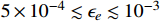 is permitted for
is permitted for
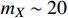 MeV of our interest.
MeV of our interest.
In this paper, we introduce two complex scalar DM particles,
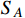 and
and
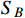 , to interpret the XENON1T excess with a light vector mediator X. The DM particles
, to interpret the XENON1T excess with a light vector mediator X. The DM particles
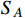 and
and
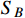 are under possible dark symmetry in the hidden sector with
are under possible dark symmetry in the hidden sector with
 , and some dark sector numbers are carried by both
, and some dark sector numbers are carried by both
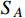 and
and
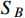 to maintain the stability of DM.
to maintain the stability of DM.
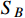 is dark charged and
is dark charged and
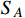 is neutral with a small mass splitting
is neutral with a small mass splitting
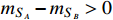 , which can be introduced from radiative corrections or substructures. The pair
, which can be introduced from radiative corrections or substructures. The pair
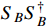 can be produced via the dark annihilation process of
can be produced via the dark annihilation process of
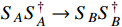 mediated by a new scalar ϕ. Thus, the present dark annihilation can provide a source of boosted
mediated by a new scalar ϕ. Thus, the present dark annihilation can provide a source of boosted
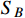 . The scattering between electron and boosted
. The scattering between electron and boosted
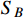 mediated by the X boson may explain the keV electron excess observed by XENON1T. In addition to the boosted
mediated by the X boson may explain the keV electron excess observed by XENON1T. In addition to the boosted
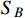 accounting for the XENON1T keV excess, there would be a fraction of un-boosted
accounting for the XENON1T keV excess, there would be a fraction of un-boosted
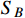 around the Earth. The relic abundance of
around the Earth. The relic abundance of
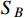 can be significantly reduced by the transition of
can be significantly reduced by the transition of
 . Thus, it will be compatible with the stringent bound on un-boosted
. Thus, it will be compatible with the stringent bound on un-boosted
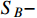 electron scattering in DM direct detections. This tangible approach is explored in this paper.
electron scattering in DM direct detections. This tangible approach is explored in this paper.
II. DM INTERACTIONS AND TRANSITIONS
In this paper, we consider a scalar DM model to interpret the XENON1T excess. In this model,
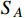 is dark neutral, and
is dark neutral, and
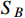 is charged under possible dark symmetry in the hidden sector.
is charged under possible dark symmetry in the hidden sector.
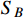 is intermediated by a new vector boson X to interact with an electron. X is assumed to couple to SM charged leptons, and the effective couplings are expressed as
is intermediated by a new vector boson X to interact with an electron. X is assumed to couple to SM charged leptons, and the effective couplings are expressed as
X is considered to be a light vector boson in general; here, we do not specify a scenario such as a kinetic mixing portal or a new gauged U
 . The dark charged
. The dark charged
 couples to the X boson via
couples to the X boson via
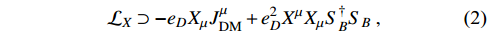
where
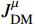 is the charged current of scalar DM
is the charged current of scalar DM
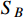 and is given by
and is given by
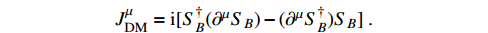
Here, we assume that the X particle has a mass
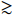 14 MeV [22] and predominantly decays into
14 MeV [22] and predominantly decays into
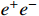 .
.
We also assume a real dark field ϕ coupled to both
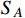 and
and
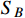 , and it mediates the transition between
, and it mediates the transition between
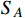 and
and
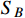 . In addition to the kinetic energy terms, the scalar Lagrangian is given by
. In addition to the kinetic energy terms, the scalar Lagrangian is given by
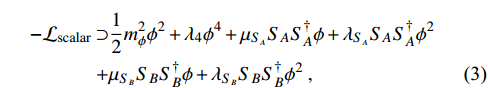
The parameters
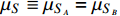 and
and
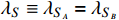 are adopted. Here, we assume
are adopted. Here, we assume
 for simplicity, and a small mass splitting Δ between
for simplicity, and a small mass splitting Δ between
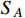 and
and
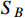 is introduced, i.e.,
is introduced, i.e.,
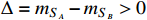 . To avoid the overabundance of ϕ in the early universe, we adopt
. To avoid the overabundance of ϕ in the early universe, we adopt
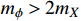 ; thus, the decay mode
; thus, the decay mode
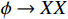 is generated at loop level from the
is generated at loop level from the
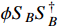 coupling and the charged current of
coupling and the charged current of
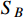 . For
. For
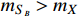 , the relic fraction of
, the relic fraction of
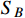 can be significantly depleted when the on-shell annihilation mode
can be significantly depleted when the on-shell annihilation mode
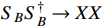 is opened. In addition, possible
is opened. In addition, possible
 SM Higgs mixing is neglected here for simplicity (for the mixing case, the mixing with a rough upper limit of
SM Higgs mixing is neglected here for simplicity (for the mixing case, the mixing with a rough upper limit of
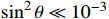 can be permitted by experiments [27]). Please note that there may be more particles in the new sector, and here we only consider the particles with key roles in transitions between the SM and dark sector.
can be permitted by experiments [27]). Please note that there may be more particles in the new sector, and here we only consider the particles with key roles in transitions between the SM and dark sector.
To induce the keV electron scattering events via boosted
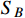 , the dark annihilation process of
, the dark annihilation process of
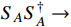 is considered to be dominant in
is considered to be dominant in
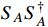 annihilation. The annihilation cross section is given by
annihilation. The annihilation cross section is given by
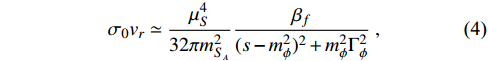
where
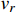 is the relative velocity, and s is the squared total invariant mass. In the non-relativistic limit, the phase space factor
is the relative velocity, and s is the squared total invariant mass. In the non-relativistic limit, the phase space factor
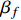 is
is
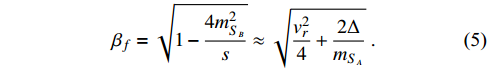
The decay width of ϕ is
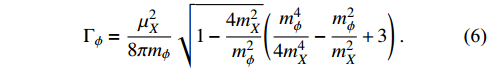
The annihilation of dark charged DM
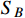 is primarily governed by
is primarily governed by
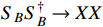 via the
via the
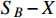 coupling in Eq. (2). The annihilation cross section is
coupling in Eq. (2). The annihilation cross section is
The
 -wave process
-wave process
 is suppressed by
is suppressed by
 and is negligible compared with the above annihilation process (see Ref. [19] for this
and is negligible compared with the above annihilation process (see Ref. [19] for this
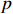 -wave dominant case).
-wave dominant case).
III. BOOSTED DM FOR THE XENON1T EXCESS
Assuming that the main component of DM is
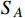 , which has a Navarro-Frenk-White (NFW) profile, the boosted DM particles
, which has a Navarro-Frenk-White (NFW) profile, the boosted DM particles
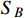 can be produced by the present dark annihilation process of
can be produced by the present dark annihilation process of
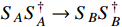 . To obtain the benchmark velocity
. To obtain the benchmark velocity
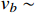 0.06 in Ref. [3] for boosted
0.06 in Ref. [3] for boosted
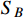 , the value of
, the value of
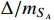 is required to be
is required to be
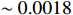 as
as
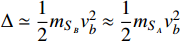 . The flux of the boosted DM
. The flux of the boosted DM
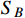 over the full sky can be expressed as [28]
over the full sky can be expressed as [28]
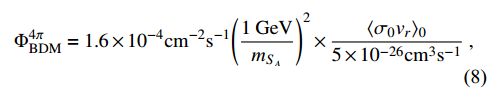
where
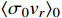 is today's thermally averaged annihilation cross section of
is today's thermally averaged annihilation cross section of
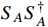 and is suppressed by the phase space factor
and is suppressed by the phase space factor
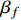 . Together with the flux of boosted DM
. Together with the flux of boosted DM
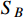 hitting the earth detectors, the number of signal events
hitting the earth detectors, the number of signal events
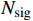 via boosted DM
via boosted DM
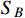 -electron scattering is
-electron scattering is
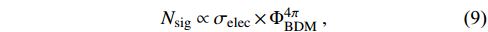
where
 is the boosted
is the boosted
 -electron scattering cross section mediated by the X boson:
-electron scattering cross section mediated by the X boson:
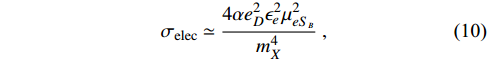
with
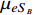 being the reduced mass of
being the reduced mass of
 and
and
 .
.
The signal events
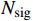 observed by XENON1T is about 40
observed by XENON1T is about 40
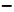 70 events. In this case, the required scattering cross section
70 events. In this case, the required scattering cross section
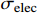 is [3]
is [3]
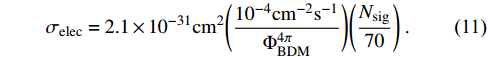
To obtain a large cross section in Eq. (10), the mass
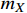 (parameter
(parameter
 ) should be as small (large) as possible. Substituting the mediator's mass
) should be as small (large) as possible. Substituting the mediator's mass
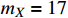 MeV,
MeV,
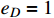 , and
, and
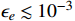 into Eq. (10), we observe that the scattering cross section
into Eq. (10), we observe that the scattering cross section
 for
for
 , and this value is smaller than the scattering cross section required by Eq. (11) even when DM mass as light as
, and this value is smaller than the scattering cross section required by Eq. (11) even when DM mass as light as
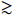 20 MeV. Thus, there is insufficient boosted
20 MeV. Thus, there is insufficient boosted
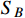 flux to produce the XENON1T excess for ordinary annihilations of
flux to produce the XENON1T excess for ordinary annihilations of
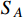 . However, if today's dark annihilation of
. However, if today's dark annihilation of
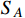 is enhanced, the result is different. We consider the annihilation of
is enhanced, the result is different. We consider the annihilation of
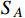 is close to the ϕ resonance with the mass
is close to the ϕ resonance with the mass
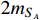 slightly above
slightly above
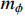 . Thus, today's dark annihilation
. Thus, today's dark annihilation
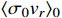 will be significantly enhanced and can produce a large flux of boosted
will be significantly enhanced and can produce a large flux of boosted
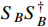 . Moreover, for DM mass
. Moreover, for DM mass
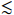 10 MeV, the scattering cross section required by Eq. (11) can be significantly lowered, while such light DM particles will be in tension with constraints from BBN and CMB.
10 MeV, the scattering cross section required by Eq. (11) can be significantly lowered, while such light DM particles will be in tension with constraints from BBN and CMB.
Now, we introduce a parameter
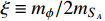 in which ξ is slightly smaller than 1. The cross section
in which ξ is slightly smaller than 1. The cross section
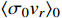 is sensitive to the value of
is sensitive to the value of
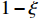 . The decay width is negligible in DM annihilations when
. The decay width is negligible in DM annihilations when
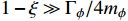 is satisfied. In the early universe, DM chemically decouples from the thermal bath when the reaction rate
is satisfied. In the early universe, DM chemically decouples from the thermal bath when the reaction rate
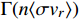 of DM particles decreases below the Hubble expansion rate H. For
of DM particles decreases below the Hubble expansion rate H. For
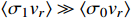 considered here, the DM
considered here, the DM
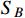 freeze-out occurs slightly later compared with the DM
freeze-out occurs slightly later compared with the DM
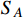 . As the mass difference between
. As the mass difference between
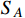 and
and
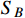 is very small, the number density is
is very small, the number density is
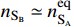 during the freeze-out period of
during the freeze-out period of
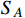 . Considering contributions from the
. Considering contributions from the
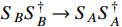 transition, the effective annihilation cross section of DM
transition, the effective annihilation cross section of DM
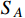 is equivalent to
is equivalent to
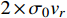 during the freeze-out period (see Appendix A for details). The relic density of DM is determined by the annihilation cross section, and it can be evaluated using the general method without s-wave approximation [29–31]. The coupling parameter
during the freeze-out period (see Appendix A for details). The relic density of DM is determined by the annihilation cross section, and it can be evaluated using the general method without s-wave approximation [29–31]. The coupling parameter
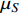 as a function of
as a function of
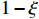 is derived with the relic density of
is derived with the relic density of
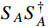 nearly equal to the total DM relic density
nearly equal to the total DM relic density
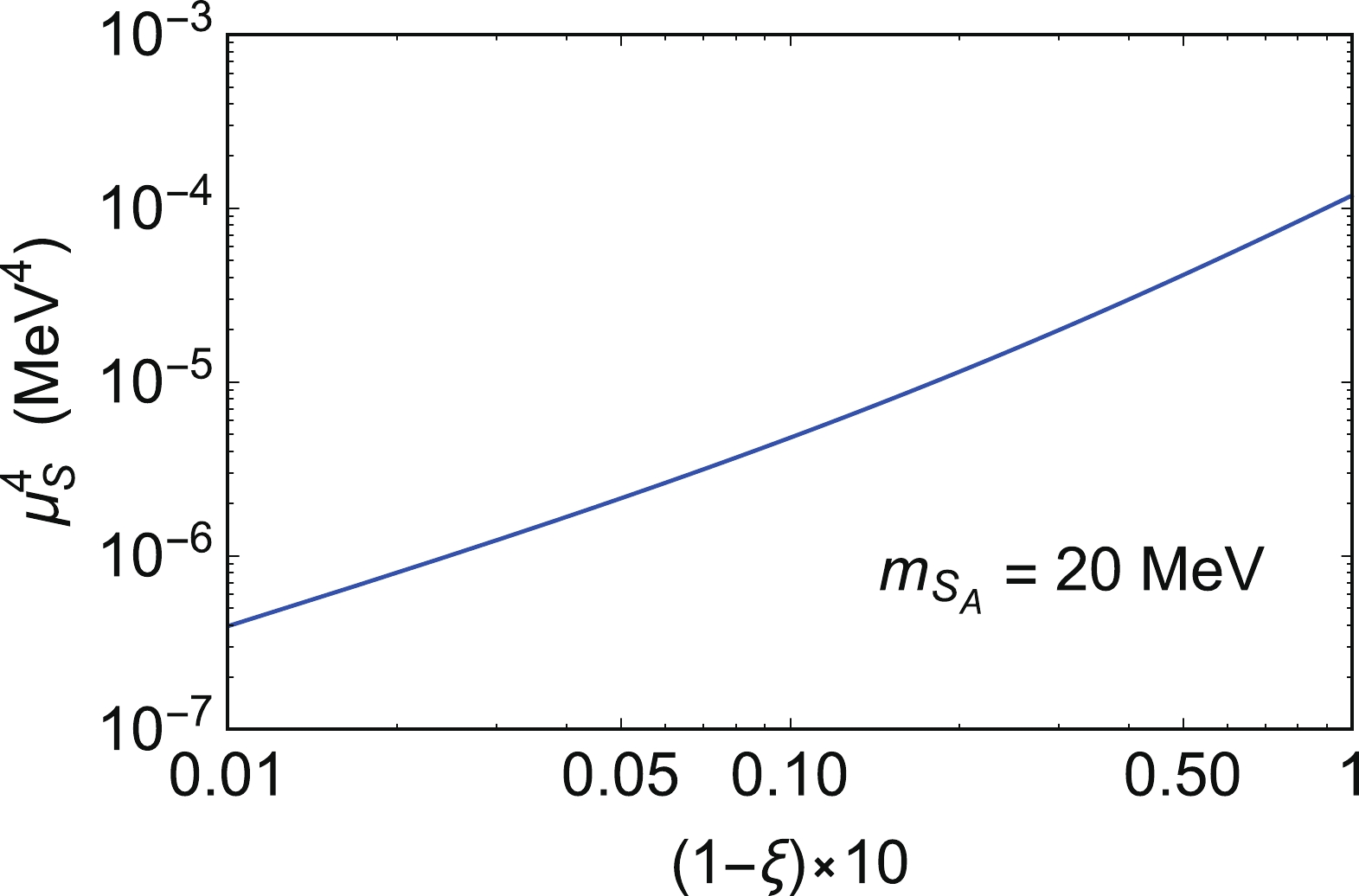
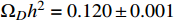 [32], as shown in Fig. 1. Today's
[32], as shown in Fig. 1. Today's
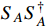 annihilation
annihilation
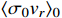 as a function of
as a function of
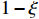 is shown in Fig. 2, with the value of
is shown in Fig. 2, with the value of
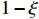 varying in a range of
varying in a range of
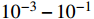 . Note that the relative velocity
. Note that the relative velocity
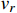 in the galaxy is
in the galaxy is
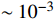 , and
, and
 is insensitive to
is insensitive to
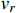 in
in
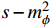 or the phase space factor
or the phase space factor
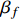 in
in
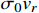 in Eq. (4) for the range of
in Eq. (4) for the range of
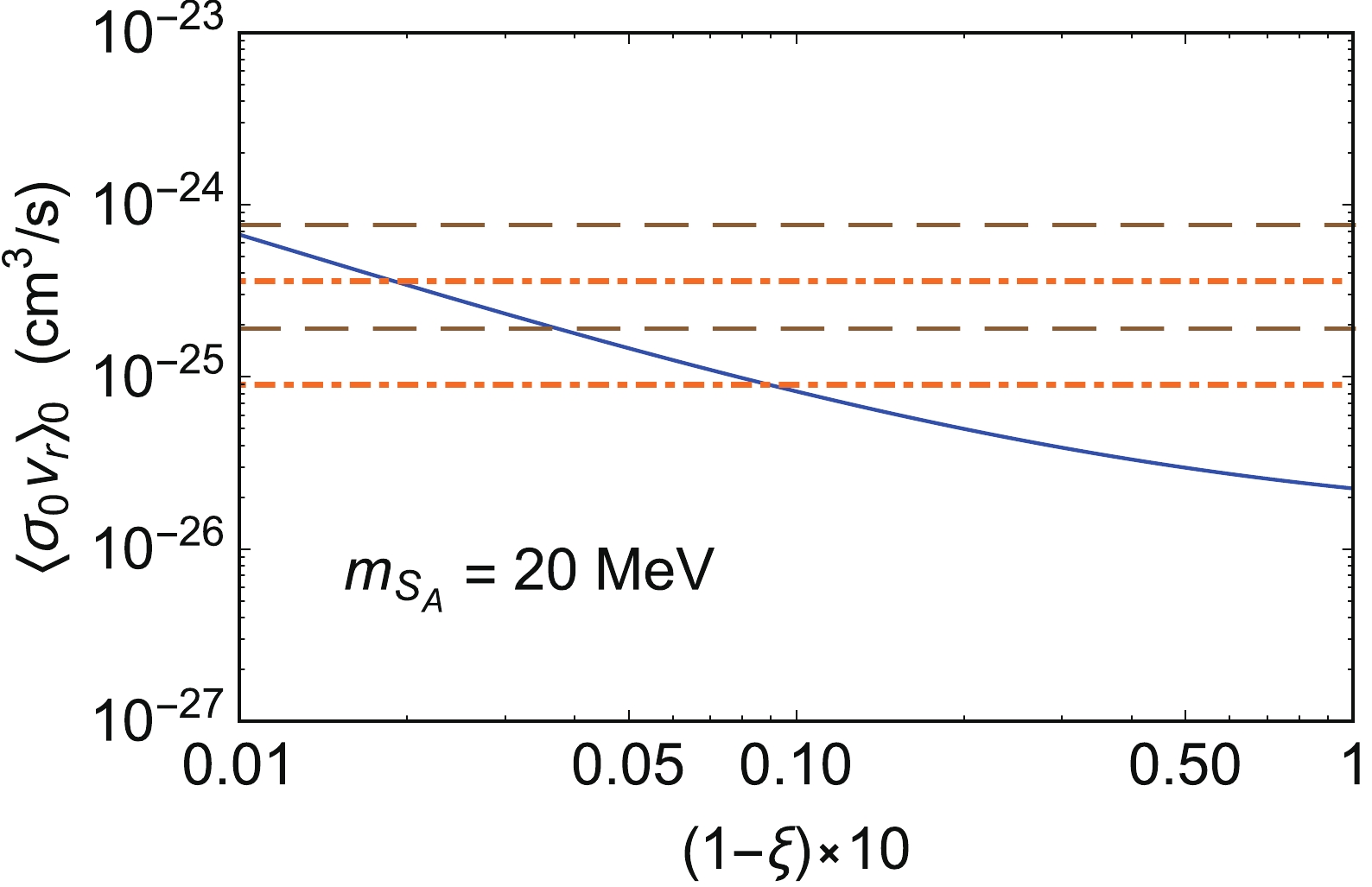
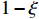 of concern. In Fig. 2, the solid curve is the corresponding
of concern. In Fig. 2, the solid curve is the corresponding
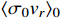 for a given
for a given
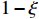 , and we observe that the annihilation is enhanced when ξ is very close to 1. The dot-dashed and dashed curves are the annihilation cross sections required by the XENON1T excess for two benchmark values of [
, and we observe that the annihilation is enhanced when ξ is very close to 1. The dot-dashed and dashed curves are the annihilation cross sections required by the XENON1T excess for two benchmark values of [
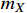 = 17 MeV,
= 17 MeV,
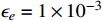 ] and [
] and [
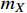 = 19 MeV,
= 19 MeV,
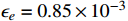 ] adopted here, respectively. We can observe that the resonance enhanced dark annihilation of today can produce large boosted
] adopted here, respectively. We can observe that the resonance enhanced dark annihilation of today can produce large boosted
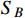 flux to account for the XENON1T excess.
flux to account for the XENON1T excess.
Fig. 1 (color online) Coupling parameter
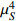 as a function of
as a function of
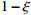 for
for
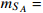 20 MeV. Here, the relic density of
20 MeV. Here, the relic density of
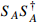 equal to 0.120 is adopted.
equal to 0.120 is adopted.
Download figure:
Standard imageFig. 2 (color online) Relation between
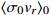 (solid curve) and
(solid curve) and
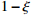 for
for
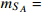 20 MeV. The dot-dashed and dashed curves are for
20 MeV. The dot-dashed and dashed curves are for
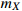 = 17 and 19 MeV, respectively. The lower (upper) limit of the dot-dashed and dashed curves corresponds to the annihilation cross sections required by the XENON1T excess for
= 17 and 19 MeV, respectively. The lower (upper) limit of the dot-dashed and dashed curves corresponds to the annihilation cross sections required by the XENON1T excess for
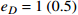 .
.
Download figure:
Standard imageNext, we briefly discuss the annihilation of
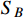 .
.
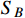 contributes only to a very small fraction
contributes only to a very small fraction
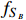 of the total DM relic density, and the relic fraction
of the total DM relic density, and the relic fraction
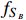 (both
(both
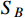 and
and
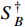 included) can be obtained using the relation
included) can be obtained using the relation
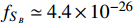 cm
cm
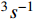 /
/
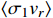 [33, 34]. The annihilation of
[33, 34]. The annihilation of
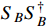 is suppressed by the factor
is suppressed by the factor
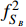 in observations, and revised annihilation cross section
in observations, and revised annihilation cross section
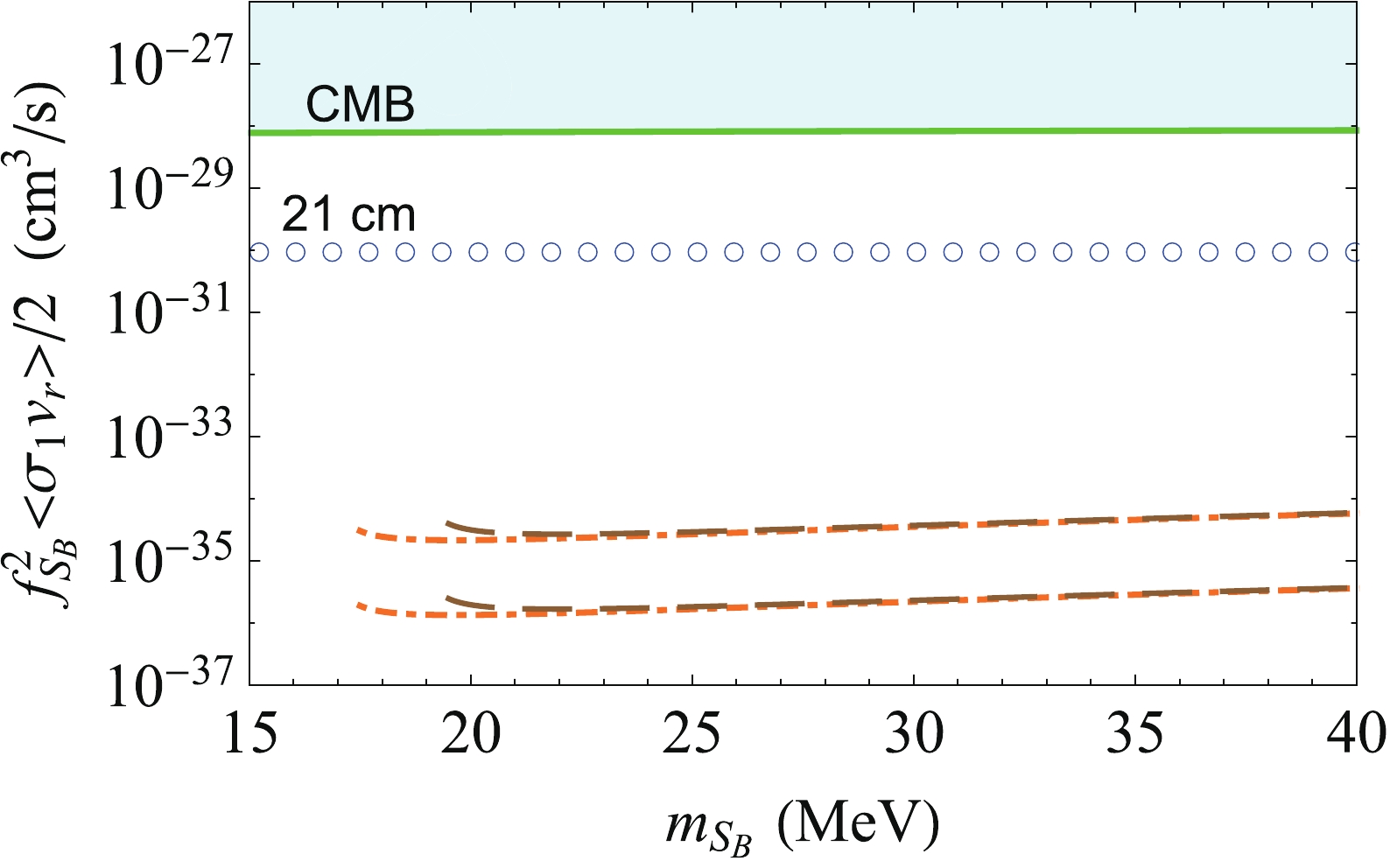
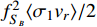 is shown in Fig. 3 for
is shown in Fig. 3 for
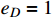 and 0.5. For two benchmark values of
and 0.5. For two benchmark values of
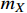 = 17 and 19 MeV, the dark matter masses
= 17 and 19 MeV, the dark matter masses
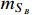 (
(
 ) in a range of
) in a range of
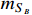 (
(
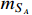 )
)
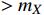 are permitted by the constraint from CMB [35] and the typical upper limit set by the anomalous 21-cm absorption [36], as depicted in Fig. 3. Given
are permitted by the constraint from CMB [35] and the typical upper limit set by the anomalous 21-cm absorption [36], as depicted in Fig. 3. Given
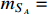 20 MeV and
20 MeV and
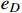 = 1,
= 1,
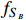 is of order
is of order
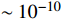 for
for
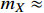 17
17
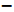 19 MeV.
19 MeV.
Fig. 3 (color online) Revised annihilation cross section
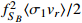 as a function of
as a function of
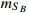 . The dot-dashed and dashed curves are the revised annihilation cross sections for
. The dot-dashed and dashed curves are the revised annihilation cross sections for
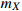 = 17 and 19 MeV, respectively. The lower (upper) limit of the dot-dashed and dashed curves corresponds to the annihilation cross sections for
= 17 and 19 MeV, respectively. The lower (upper) limit of the dot-dashed and dashed curves corresponds to the annihilation cross sections for
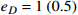 . The solid curve is the constraint from CMB [35], and the empty dotted curve is the typical upper limit set by the anomalous 21-cm absorption with
. The solid curve is the constraint from CMB [35], and the empty dotted curve is the typical upper limit set by the anomalous 21-cm absorption with
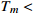 4 K at z = 17.2 [36].
4 K at z = 17.2 [36].
Download figure:
Standard imageIV. DIRECT DETECTION OF UN-BOOSTED DM
In addition to the boosted
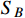 accounting for the XENON1T keV excess, a large amount of
accounting for the XENON1T keV excess, a large amount of
 and
and
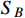 with a regular velocity distribution are present around the earth. Now, we discuss the un-boosted DM-electron scattering. First, we consider the un-boosted
with a regular velocity distribution are present around the earth. Now, we discuss the un-boosted DM-electron scattering. First, we consider the un-boosted
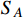 .
.
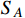 -electron scattering occurs at two-loop level from the
-electron scattering occurs at two-loop level from the
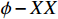 transition and
transition and
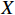 -electron coupling. The scattering cross section is significantly below the neutrino floor [37, 38] in DM direct detections.
-electron coupling. The scattering cross section is significantly below the neutrino floor [37, 38] in DM direct detections.
For the un-boosted
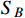 , the
, the
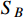 -electron scattering is primarily contributed by the tree level process mediated by the X boson. The corresponding scattering cross section is
-electron scattering is primarily contributed by the tree level process mediated by the X boson. The corresponding scattering cross section is
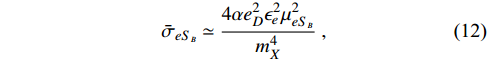
with the form factor
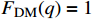 [39]. For
[39]. For
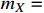 17 MeV,
17 MeV,
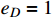 , and
, and
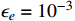 , the scattering cross section is
, the scattering cross section is
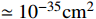 , which is above the bound set by XENON10/100 [10, 11]. This is why the ordinary interpretation of the XENON1T keV excess via DM-electron scattering appears to be in tension with DM direct detections, although DM mass is as low as
, which is above the bound set by XENON10/100 [10, 11]. This is why the ordinary interpretation of the XENON1T keV excess via DM-electron scattering appears to be in tension with DM direct detections, although DM mass is as low as
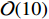 MeV. In this paper, the DM particles
MeV. In this paper, the DM particles
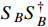 constitutes only a very small fraction
constitutes only a very small fraction
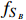 of the total DM; thus, the tension can be relaxed owing to the effective scattering cross section being
of the total DM; thus, the tension can be relaxed owing to the effective scattering cross section being
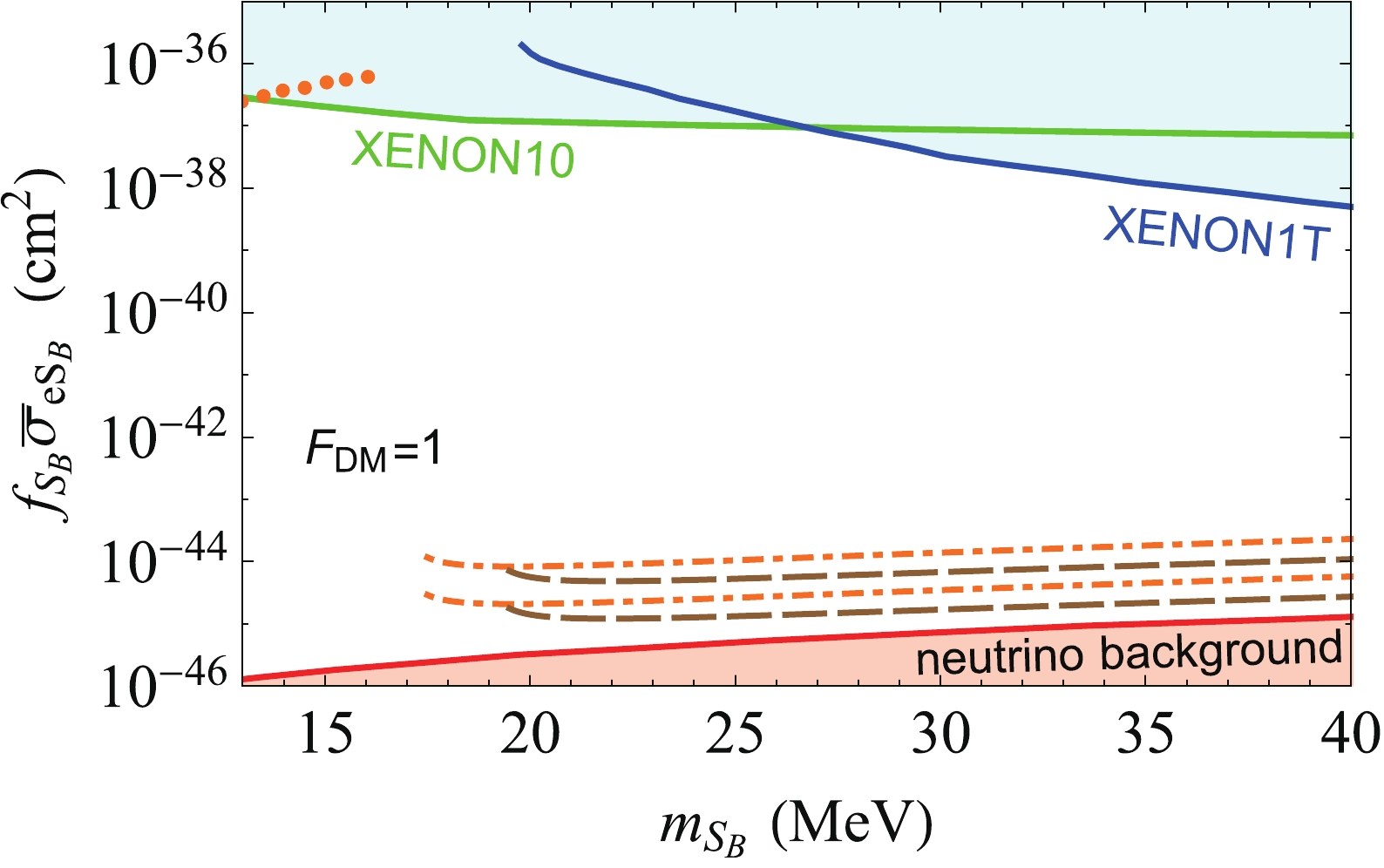
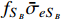 in DM direct detections. The result of the effective scattering cross section
in DM direct detections. The result of the effective scattering cross section
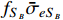 is shown in Fig. 4. We can observe that the benchmarks we consider above can evade the constraints from CMB, 21 cm absorption, and DM direct detections.
is shown in Fig. 4. We can observe that the benchmarks we consider above can evade the constraints from CMB, 21 cm absorption, and DM direct detections.
Fig. 4 (color online) Effective scattering cross section
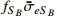 as a function of
as a function of
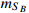 for un-boosted
for un-boosted
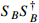 in DM direct detections. The dot-dashed and dashed curves are the effective scattering cross section for the benchmark values as labeled in Figs. 2 and 3. The lower (upper) limit of the dot-dashed and dashed curves correspond to the cross sections for
in DM direct detections. The dot-dashed and dashed curves are the effective scattering cross section for the benchmark values as labeled in Figs. 2 and 3. The lower (upper) limit of the dot-dashed and dashed curves correspond to the cross sections for
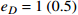 . The upper two solid curves are the upper limits from XENON10 [11] and XENON1T [13]. For comparison, the dotted curve on the top left is for
. The upper two solid curves are the upper limits from XENON10 [11] and XENON1T [13]. For comparison, the dotted curve on the top left is for
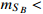
 MeV [19]. The lower solid curve is the neutrino background [37].
MeV [19]. The lower solid curve is the neutrino background [37].
Download figure:
Standard imageMoreover, for
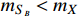 , sufficiently boosted
, sufficiently boosted
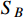 can also be produced, and it induces the XENON1T keV excess. The mass
can also be produced, and it induces the XENON1T keV excess. The mass
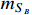 should be
should be
 13 MeV given the constraints from DM direct detections, as shown by the dotted curve in Fig. 4. Meanwhile, for
13 MeV given the constraints from DM direct detections, as shown by the dotted curve in Fig. 4. Meanwhile, for
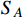 and
and
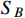 , the mass
, the mass
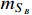 (
(
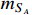 ) should be
) should be
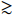 13 MeV with the bound from BBN [17]. Thus, a very small parameter space remains for the case of
13 MeV with the bound from BBN [17]. Thus, a very small parameter space remains for the case of
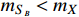 when interpreting the XENON1T keV excess, and this case is beyond the scope of this paper.
when interpreting the XENON1T keV excess, and this case is beyond the scope of this paper.
V. CONCLUSION
The boosted DM with a high speed of about 0.05-0.1 c and with a large DM-electron scattering cross section (as large as
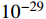 cm2 [3]) can interpret the XENON1T electron-event anomaly, as discussed in Refs. [2, 3]. However, can the boosted DM with such a large DM-electron scattering cross section be compatible with the present stringent bounds, such as the BBN, low energy experiments, and DM direct detections? This key question should be answered when proposing a model to explain the XENON1T anomaly. In this paper, we attempt to answer this question. The proposed GeV DM has a large scattering cross section (
cm2 [3]) can interpret the XENON1T electron-event anomaly, as discussed in Refs. [2, 3]. However, can the boosted DM with such a large DM-electron scattering cross section be compatible with the present stringent bounds, such as the BBN, low energy experiments, and DM direct detections? This key question should be answered when proposing a model to explain the XENON1T anomaly. In this paper, we attempt to answer this question. The proposed GeV DM has a large scattering cross section (
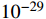 cm2) between DM and an electron [3]. The required mediator mass is as light as 0.1 MeV. Such a light mediator is excluded by the BBN, which sets a lower mass bound on new thermal equilibrium particles, that is, the mass of a new particle should be above 10 MeV. Considering the constraints from BBN and low energy experiments, we observe that the scattering cross section between DM and an electron is smaller in reality, approximately smaller than
cm2) between DM and an electron [3]. The required mediator mass is as light as 0.1 MeV. Such a light mediator is excluded by the BBN, which sets a lower mass bound on new thermal equilibrium particles, that is, the mass of a new particle should be above 10 MeV. Considering the constraints from BBN and low energy experiments, we observe that the scattering cross section between DM and an electron is smaller in reality, approximately smaller than
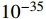 cm2. We observe that light DM in the MeV scale with an enhanced annihilation source and a scattering cross section of
cm2. We observe that light DM in the MeV scale with an enhanced annihilation source and a scattering cross section of
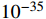 cm2 can produce sufficient keV electron excess events observed by XENON1T and be permitted by present DM direct detections.
cm2 can produce sufficient keV electron excess events observed by XENON1T and be permitted by present DM direct detections.
We have investigated an interpretation of the XENON1T excess using two scalar DM particles,
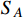 and
and
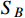 .
.
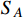 is neutral and
is neutral and
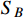 is dark charged in the hidden sector. The boosted
is dark charged in the hidden sector. The boosted
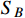 can be produced by the annihilation
can be produced by the annihilation
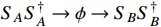 mediated by a scalar ϕ.
mediated by a scalar ϕ.
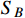 -electron scattering is intermediated by a vector boson X. We focus on the range
-electron scattering is intermediated by a vector boson X. We focus on the range
 . Although the constraints from BBN, CMB, and low-energy experiments require the boosted
. Although the constraints from BBN, CMB, and low-energy experiments require the boosted
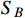 -electron scattering cross section mediated by X to be
-electron scattering cross section mediated by X to be
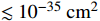 , MeV-scale DM with a resonance enhanced dark annihilation today can still produce sufficient boosted DM and induce the XENON1T keV electron excess. The relic density of
, MeV-scale DM with a resonance enhanced dark annihilation today can still produce sufficient boosted DM and induce the XENON1T keV electron excess. The relic density of
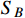 can be significantly reduced by the
can be significantly reduced by the
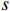 -wave process of
-wave process of
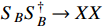 ; thus, this
; thus, this
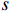 -wave annihilation is permitted by the constraints from CMB and 21-cm absorption. A very small relic fraction of
-wave annihilation is permitted by the constraints from CMB and 21-cm absorption. A very small relic fraction of
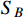 is compatible with the stringent bound on un-boosted
is compatible with the stringent bound on un-boosted
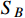 -electron scattering in DM direct detections. The
-electron scattering in DM direct detections. The
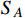 -electron scattering occurs at loop level, and the scattering cross section is below the neutrino floor in direct detections. We look forward to the further investigation of MeV DM and the corresponding new interactions in the future.
-electron scattering occurs at loop level, and the scattering cross section is below the neutrino floor in direct detections. We look forward to the further investigation of MeV DM and the corresponding new interactions in the future.
APPENDIX A: THE FREEZE-OUT OF

For
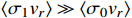 , the freeze-out of DM
, the freeze-out of DM
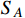 occurs first, and the DM
occurs first, and the DM
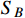 decouples from the thermal bath later. For the DM particle
decouples from the thermal bath later. For the DM particle
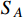 , the evolution of the number density
, the evolution of the number density
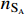 is given by
is given by
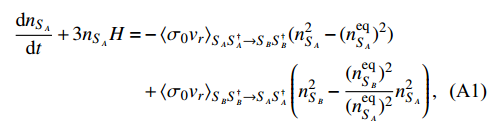
where
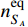 and
and
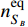 are the equilibrium number densities, and H is the Hubble parameter. The DM particle
are the equilibrium number densities, and H is the Hubble parameter. The DM particle
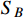 is still in the thermal equilibrium with the thermal bath during the freeze-out period of
is still in the thermal equilibrium with the thermal bath during the freeze-out period of
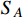 , and in this case, we obtain the number density
, and in this case, we obtain the number density
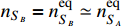 with ignorable mass difference between
with ignorable mass difference between
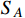 and
and
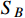 . Thus, Eq. (A1) can be rewritten as
. Thus, Eq. (A1) can be rewritten as
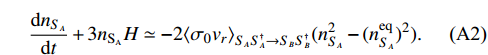
For DM
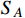 , the effective annihilation cross section is equivalent to
, the effective annihilation cross section is equivalent to
 during the freeze-out period for the
during the freeze-out period for the
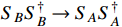 transition considered.
transition considered.
Footnotes
- *
The work of T. Li was supported by the National Natural Science Foundation of China (11975129, 12035008) and "the Fundamental Research Funds for the Central Universities", Nankai University (63196013). L.-B. Jia acknowledges support from the Longshan academic talent research supporting program of SWUST (18LZX415)