Avoiding a Cluster Catastrophe: Retention Efficiency and the Binary Black Hole Mass Spectrum

The population of binary black hole (BBH) mergers identified by the LIGO–Virgo gravitational-wave (GW) interferometer network has uncovered interesting and unexpected features in the intrinsic properties of black holes (BHs) in the universe. The LIGO Scientific and Virgo Collaboration (LVC) (Abbott et al. 2020, 2021a, 2021b), as well as groups external to the LVC (Venumadhav et al. 2020; Nitz et al. 2021), has reported a number of component BHs with significant posterior support for masses ≳50 M_⊙, in tension with predictions for the mass limit imposed by the pair-instability (PI) process (Woosley 2017, 2019; Marchant et al. 2019; Renzo et al. 2020). Though uncertainties in the underlying physical processes that lead to this phenomenon (Farmer et al. 2020; Woosley & Heger 2021) and alternative astrophysical prior interpretations (Fishbach & Holz 2020; Nitz & Capano 2021) put into question the putative observations of BHs in the PI mass gap, mergers in dense stellar environments offer a natural means of polluting this anticipated dearth in the BH mass spectrum.

In dense stellar environments such as globular clusters (GCs), nuclear clusters (NCs), and active galactic nucleus (AGN) disks, BH progenitors and BHs themselves dynamically interact and merge with other members of the cluster. Merging stars may maintain low enough He-core masses to avoid disruption through PI, leading to BHs that have masses well above the PI limit theorized for massive stars (Spera et al. 2019; di Carlo et al. 2019; Kremer et al. 2020; Di Carlo et al. 2021;Banerjee 2021; Tagawa & Kocsis 2021; González et al. 2021). Alternatively, BHs that merge within the cluster can be retained in the cluster environment and proceed to merge again with other members of the cluster, leading to increasingly massive BH mergers. This merger pathway, known as hierarchical mergers, has been shown to efficiently pollute the PI mass gap (Fishbach et al. 2017; Gerosa & Berti 2017, 2019; Rodriguez et al. 2019; Yang et al. 2019b; Kimball et al. 2020; Doctor et al. 2021; Fragione et al. 2022; Mapelli et al. 2021, 2022), and the occurrence of hierarchical mergers across various dynamical environment may help to explain the origin of certain GW events (e.g., Rodriguez et al. 2020; Baibhav et al. 2021; Fragione & Loeb 2021; Gayathri et al. 2021; Gerosa & Fishbach 2021; Kimball et al. 2021; Tagawa et al. 2021; Wong et al. 2021; Zevin et al. 2021). This process has also been invoked to explain the growth of intermediate-mass black holes (IMBHs) in cluster environments (Quinlan & Shapiro 1987) and might be assisted by repeated stellar mergers prior to the collapse of the IMBH seed (e.g., Portegies Zwart & McMillan 2002; Gurkan et al. 2004; Giersz et al. 2015; Freitag et al. 2006; Kremer et al. 2020; Di Carlo et al. 2021; González et al. 2021; Fragione 2022; Fragione et al. 2022).

The efficiency of this channel is highly dependent on the global properties of a cluster environment; when two BHs merge, anisotropies in GW emission impart momentum to the merger product known as a gravitational recoil kick or radiation rocket (Favata et al. 2004), which is amplified by asymmetries in the masses and spins of the system. If this kick exceeds the escape velocity of their host environment, the BH merger product will be ejected and will be incapable of encountering another BH with which to merge again (Merritt et al. 2004). Higher-density environments such as NCs and AGNs will thus be much more efficient at retaining merger products than lower-mass GCs (Gerosa & Berti 2019), and the 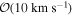escape velocities of young star clusters and open clusters will hardly be able to retain any merger products whatsoever. Inference on the recoil kick velocities of BBH mergers has found that an appreciable number of merger products from recent GW catalogs should be retained by their host environments if they merged in star clusters (Mahapatra et al. 2021).

A natural inclination would be to attribute the higher-mass systems observed by the LVC to such high-mass and high-density environments. However, this interpretation must be exercised with caution. If a particular environment is too efficient at retaining merger products, it may lead to runaway BH mergers and a cluster catastrophe (Fishbach et al. 2017). In this case, the predicted mass spectrum may have an overabundance of high-mass mergers that is inconsistent with the observed masses of GW events. Ground-based GW interferometers are more sensitive to higher-mass BH mergers (up to a certain point), and selection effects must be accounted for when comparing BH population predictions to the catalog of observed systems.

In this paper, we use simple models for hierarchical mergers to demonstrate how the expected mass spectrum of hierarchical mergers is impacted by aspects of the host environment, with a particular focus on how environments with high retention efficiencies can potentially produce an overabundance of high-mass mergers that are inconsistent with the empirical BH mass spectrum. The relative lack of high-mass merger observations can thereby place constraints on the contribution of hierarchical mergers from certain dynamical environments to the full BBH population. In Section 2 we outline our models and model assumptions, and discuss how hierarchical merger trees are constructed. We present the results from our models in Section 3, highlighting the impact of escape velocity on the predicted BH mass spectrum. We conclude with implications and caveats of our analysis in Section 4.

The primary goal of this work is to investigate how host cluster properties, in particular escape velocities, impact the observed mass spectrum of hierarchically merging BBHs. We pre-generate merger trees that start with first-generation (1G) BH seeds and grow them by merging BHs in series while tracking pertinent properties of their remnants. A number of different pairing assumptions for hierarchical mergers are used as a representation of the pairing processes in dynamical formation environments of BBHs. We then prune the merger trees to account for the escape velocity of host environments as well as the budget of BHs available in a particular environment. Finally, we apply selection effects to a compiled population of hierarchical mergers and compare the resulting mass distributions to those observed by LIGO–Virgo. Our models are similar in construction to those in Gerosa et al. (2021). The codebase for performing our analysis is available on Github, ⁵ with data products used in our analyses available on Zenodo. ⁶

2.1. Initial Population of Black Holes

2.2. Synthesizing Merger Trees

Branches of a merger tree represent a single chain of hierarchical mergers. Each branch is initially grown with no limitations from escape velocity or an assumed maximum number of BHs that can partake in the hierarchical assembly. We assume three distinct pairing methods for growing each individual hierarchical merger branch:

• 1.  
  NG+1G: The merger product being tracked continually merges with other BHs from the 1G distribution. As hierarchical mergers produce successive populations of larger BHs, we repeatedly and exclusively pair these NG BHs with either the primary or secondary BH from the original (1G) distribution. This method resembles the expectations of a runaway merger scenario, which has been invoked for forming IMBHs (Quinlan & Shapiro 1987; Miller & Hamilton 2002), as well as the assembly of hierarchical BHs in the migration traps of AGN disks (e.g., McKernan et al. 2014; Yang et al. 2019b; McKernan et al. 2020; Tagawa et al. 2021; Li 2022).
• 2.  
  NG+NG: The merger product being tracked continually merges with another BH that has gone through the same number of prior mergers. This expedites the buildup in mass of the merger product and resembles the expectations from dense stellar environments where the most massive objects mass-segregate and dominate the dynamics of the dense cluster core, preferentially kicking out lighter components during strong few-body gravitational encounters.
• 3.  
  NG+ ≤ NG: The merger product being tracked merges with a BH that has gone through a number of mergers M ≤ N. The probability that a given merger generation M is chosen for the companion is proportional to the number of 1G BHs required to synthesize it, p(M) ∝ 2^−(M−1) (for example, the NG BH is twice as likely to merge with a 1G BH than a 2G BH, and four times as likely to merge with a 1G BH than a 3G BH). If the merger partner is chosen to be a 1G BH, in the LVC model we once again split up the primary and secondary components and randomly choose one. This is representative of a steady-state limit and is a useful model for means of comparison with the other pairing models.

Note that the term “generation” becomes ambiguous once one exceeds 2G mergers; a 3G merger in the NG+1G channel requires four 1G BHs, whereas a 3G merger in the NG+NG channel requires 2 × 2³ = 16 1G BHs. Thus, for the majority of this work, we will instead refer to the number of mergers, N_merge, that have occurred at a particular point along a branch.

Our simple model also requires a prescription to determine the amount of time that passes between subsequent mergers. This will impact the number of hierarchical mergers that can occur before the present day and potentially be detected via GWs. For our fiducial model, we assume that delay times between each subsequent merger, 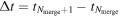, are drawn from a log-uniform distribution between 10 and 100 Myr. Merger redshifts are determined assuming Planck cosmological parameters (Planck Collaboration et al. 2020).

Our choice of delay-time distribution is representative of young massive clusters and GCs, in which BHs have relatively short mass segregation timescales of ∼10–100 Myr (e.g., Portegies Zwart et al. 2010). We note that this is a simplifying assumption because the dynamical friction timescale can vary vastly between different host environments (Antonini et al. 2019; Fragione & Silk 2020; Fragione et al. 2022), and other functional forms for the delay times between subsequent mergers may lead to differences in our underlying and detectable populations. In Appendix A, we test the sensitivity of our main results to variations in the assumed delay-time distribution, using extended log-uniform distributions between [10 Myr, 1 Gyr] and [100 Myr, 14 Gyr]. Though the first of these variations has little impact on results, the second variation acts to suppress the highest mass mergers in our hierarchical scenarios because these will more readily occur at times beyond the present day; see Figure 5 in Appendix A.

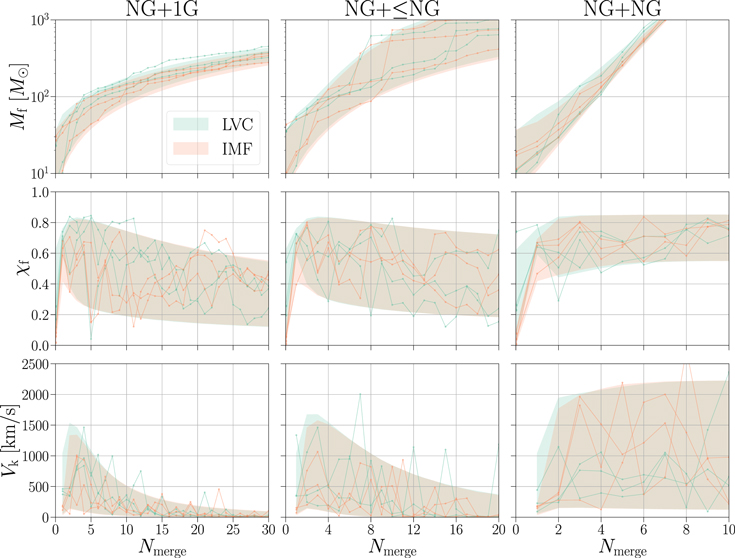
For each merger, we determine the mass of the merger product M_f, the spin of the merger product χ_f, and the GW recoil kick velocity V_k using the precession package (Gerosa & Kesden 2016). We also track the number of 1G BHs needed to generate each merger product, defined as N_1G (e.g., for the merger product of a 2G +2G merger, N_1G = 4 since 4 1G BHs are utilized). We grow 5 × 10⁵ such branches for each merger tree, allowing for 10, 20, and 30 subsequent mergers on each branch for the NG+NG, NG+ ≤ NG, and NG+1G scenarios, respectively, ⁷ and combine their results when synthesizing our populations. The evolution of relevant parameters as a function of N_merge is shown in Figure 1.

Zoom In Zoom Out Reset image size

2.3. Pruning Merger Trees

2.4. Selection Effects

Finally, we incorporate selection effects on the remaining population as a means to compare our models with the empirical distribution of BBHs mergers. Our semianalytic treatment of selection effects uses a precomputed grid of LIGO–Virgo detection probabilities, 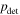, over chirp mass 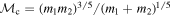, mass ratio q = m₂/m₁ with m₂ ≤ m₁, and redshift z, where m₁ and m₂ are the primary and secondary masses, respectively (Zevin 2021). We ignore spin effects and possible eccentricity in the detectability calculations. Our grids assume a three-detector network consisting of LIGO–Livingston, LIGO–Hanford, and Virgo operating at midhigh/latelow sensitivity (Abbott et al. 2018), with a network detection threshold of signal-to-noise ratio > 10. Relative detection weights for each merger also account for surveyed spacetime volume:

where dV_c /dz is the differential comoving volume at redshift zⁱ and (1 + z)⁻¹ accounts for time dilation between the merger and the detectors. We assume a primary mass detection cutoff of 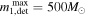—any system with a (detector-frame) primary mass 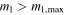has a detection probability of zero, because beyond this the detector spectral sensitivity drops significantly (e.g., Mehta et al. 2022).

We first examine general features of the hierarchical merger trees without incorporating constraints based on the host environment: We assume no merger products are ejected from their host environment and that there is an infinite budget of BHs with which to merge (see Figure 1). Merger product masses grow exponentially for the NG+NG pairing, approximately doubling in mass with each subsequent merger, whereas the relative mass growth flattens in both the NG+ ≤ NG and NG+1G cases. The merger trees that result from the IMF initial mass distribution push to slightly lower masses than the LVC initial mass distribution because it has no support for component masses above 50 M_⊙ in the 1G population. The median source-frame mass of the merger product exceeds 100 M_⊙ after nine, six, and four mergers for both the LVC and IMF initial mass distributions in the NG+1G, NG+ ≤ NG, and NG+NG cases, respectively.

Merger product spins rise to ∼0.7 after the first merger due to the orbital angular momentum of the merging binary (Fishbach et al. 2017), with a dispersion due to asymmetries in the component masses and the spin orientations of the mergers. The distribution of merger product spins remains peaked at ∼0.7 for the NG+NG pairing scenario because mergers are typically near equal mass. However, average merger product spins decrease as a function of N_merge in the NG+1G and NG+ ≤ NG cases; though aligned and antialigned spins are equally likely in an isotropic spin distribution, counterrotating orbits are more efficient at extracting angular momentum than corotating orbits are at depositing it (Hughes & Blandford 2003). To first order, the decrease in BH spin is proportional to the mass ratio of the binary and thus on average the spin distribution of merger products will approach zero after many mergers with asymmetric masses (e.g., Fragione et al. 2022; Gerosa et al. 2021). For NG+1G and NG+ ≤ NG, the spin of the merger products drops below 0.5 after ∼8 and ∼14 mergers, respectively. Though this work focuses on mass distributions through hierarchical assembly, a population of hierarchical mergers will also display distinctive spin signatures, such as high spins that are oriented in the hemisphere opposite of the orbital angular momentum, which may also be used to constrain the abundance of hierarchical BBH mergers in the general population (see, e.g., Fishbach et al. 2022).

Recoil kick velocities, as well as the dispersion of the recoil kick velocity distribution, also decrease as a function of N_merge in the NG+1G and NG+ ≤ NG pairings. Though mergers with nonspinning components will have a maximum kick at a mass ratio of 0.36 (e.g., Favata et al. 2004), the strength of the recoil kick drops precipitously as the mass ratio approaches zero even if the component BHs have significant spin. For NG+1G and NG+ ≤ NG pairings, median recoil kicks drop below 300 km s⁻¹ after ∼3–4 mergers. However, recoil kicks stay relatively strong with a broad distribution ranging from ∼100–2100 km s⁻¹ in the NG+NG case due to its preference for near-equal-mass pairings.

3.1. Imposing Escape Velocities

Escape velocities in dynamical environments that potentially harbor BHs can range from 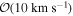for present-day GCs to 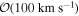for NCs, and up to ∼1000 km s⁻¹ in AGN disks. Though host escape velocities can evolve significantly in time (for example, present-day GCs may have been a few times more massive at birth with escape velocities of several hundred km s⁻¹; Webb & Leigh 2015), we postprocess our merger trees assuming fixed escape velocities that are representative of different dynamical environments at specific points in their evolution. The fraction of retained merger products for various assumed escape velocities is shown in Figure 2.

Zoom In Zoom Out Reset image size

For the NG+NG pairing scenario, the retention fraction drops precipitously as the number of subsequent mergers increases due to near-equal-mass mergers continuously receiving large kicks (see Figure 1). Environments with exceptionally large escape velocities can still retain a number of subsequent mergers in this scenario. For escape velocities ≳1000 km s⁻¹ and the LVC (IMF) 1G populations, 18% (19%) of hierarchical BBH systems can be retained in their host environment even after they have gone through five prior mergers, whereas this number drops to 1.2% (1.7%) for escape velocities of 500 km s⁻¹ and 0.06% (0.13%) for escape velocities of 300 km s⁻¹.

Contrary to the NG+NG pairing scenario, the retention fractions of NG+1G and NG+ ≤ NG scenarios tend to level out after a number of subsequent mergers have been lucky enough to be retained in their host environments. This behavior is particularly apparent for high escape velocities in the NG+1G pairing because the buildup of the merger product mass will result in extreme mass ratios that receive negligible kicks upon merging with a member of the 1G population. For the NG+1G pairing and the LVC (IMF) 1G population at escape velocities of ≳100 km s⁻¹, 48% (59%) of merger products are retained forever, never having been ejected from their host environment. This percentage is still substantial for escape velocities down to 300 km s⁻¹, with 8% (13%) and 1% (2%) of systems never being ejected for environments with escape velocities of 500 km s⁻¹ and 300 km s⁻¹, respectively.

The coevolution of mass growth and recoil kick strength as the number of mergers increases leads to the efficient buildup of merger product mass for moderate to high escape velocities in each pairing scenario considered. For NG+1G pairing, the rate of mass growth of the hierarchical merger product is slower, though the retention efficiency is much higher and can lead to long chains of subsequent mergers that can cause significant buildup in mass. Though less efficient at retaining merger products, the mass buildup in the NG+NG pairing is expedited due to pairings that tend to be near equal in mass. The NG+ ≤ NG scenario exhibits a mix of both of these general features. In the following subsection, we turn to the expected mass distributions of hierarchically assembled BHs when escape velocities are incorporated and compare them with the empirical mass distribution from current GW observations.

3.2. Mass Distributions through Hierarchical Assembly

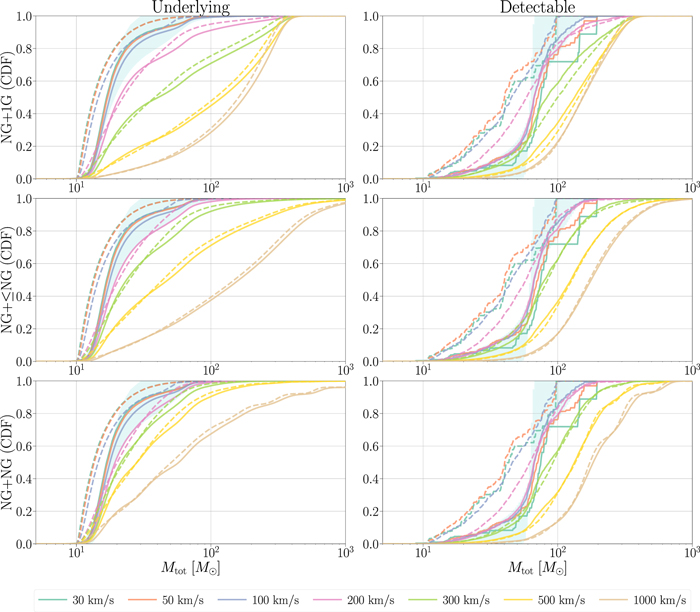
We now examine the resultant mass distributions of our hierarchically assembled BHs using various assumptions for the escape velocity of their host environments. Mirroring the results of Figure 2, the total mass distributions in Figure 3 push to larger values as the escape velocities of their hosts increase due to longer chains of hierarchical mergers being retained. For example, using the LVC 1G population and the NG+1G pairing, we find that 34% of hierarchical mergers have a source-frame total mass >80 M_⊙ for escape velocities of 300 km s⁻¹, 61% for escape velocities of 500 km s⁻¹, and 78% for escape velocities of 1000 km s⁻¹.

Zoom In Zoom Out Reset image size

Due to the Malmquist bias inherent to compact binary mergers, more massive mergers are more luminous, which pushes the detectable mass distribution to higher values. However, due to seismic noise that impinges Earth-based detectors, BBHs above a certain detector-frame mass will merge at too low of a GW frequency to be detected. Thus, the cumulative distribution functions (CDFs) of the detectable distributions plateau at M_tot ≳ 500 M_⊙. For the LVC 1G population and the NG+1G pairing, we find that 52%, 76%, and 87% of detectable hierarchical mergers have source-frame total masses >80 M_⊙ for escape velocities of 300 km s⁻¹, 500 km s⁻¹, and 1000 km s⁻¹, respectively.

Mass distributions push to lower values when considering the IMF 1G population as opposed to the LVC 1G population. This is due to the IMF population having a steeper power-law slope and truncating at a lower maximum mass. Though natal spins are lower for the IMF 1G population (and thus kicks are suppressed, the bottom row of Figure 1), initial spins are mostly washed out after the first merger and the drop of retention efficiency for subsequent mergers follows a similar behavior as the LVC model (Figure 2).

We emphasize that these mass distributions only consider BBH mergers formed through hierarchical assembly, thus ignoring the potential additional contribution of “1G+1G” mergers in the same dynamical environment as well as other formation channels that may contribute to the full BBH population, such as mergers that result from isolated field binaries. Therefore, the level of inconsistency between the empirical LVC distribution and the mass distributions we construct act to jointly constrain the branching fraction of a particular dynamical formation channel as well as the fraction of BBH mergers within that channel that are the result of hierarchical assembly relative to “1G+1G” mergers.

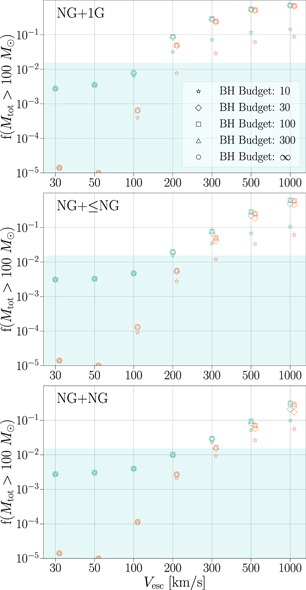
Figure 4 shows the expected fraction of mergers above a source-frame total mass of 100 M_⊙ as a function of escape velocity predicted by our hierarchical merger models. The cyan band indicates the number of BBH mergers with a total source-frame mass >100 M_⊙ based on the posterior predictive distribution measured using the Power Law + Peak mass model in the LVC analysis (Abbott et al. 2021c); <1.5% of BBH mergers have a total source-frame masses greater than 100 M_⊙ at 95% credibility. For most pairing models, once escape velocities reach ∼300 km s⁻¹, the fraction of hierarchically assembled systems with total masses greater than 100 M_⊙ exceeds the upper limit measured in the LVC mass distribution. The exception is the NG+NG pairing model with the IMF 1G population, where even at an escape velocity of 300 km s⁻¹ the percentage of hierarchically assembled systems with M_tot > 100M_⊙ is 1.6%. Pairing methods that prefer symmetric masses in mergers always have a lower fraction of high-mass systems; though the buildup in mass is expedited (Figure 1), recoil kicks are consistently higher and merger products are more readily ejected (Figure 2) which suppresses the high end of the mass spectrum. For example, at an escape velocity of 500 km s⁻¹ the percentage of hierarchically assembled mergers with source-frame total masses greater than 100 M_⊙ is 9.6%, 29%, and 55% for NG+NG, NG+ ≤ NG, and NG+1G, respectively.

Zoom In Zoom Out Reset image size

Another parameter that acts to suppress the high end of the mass spectrum is the overall budget of BHs available for hierarchical assembly. The effect of imposing a BH budget is shown with different symbols in Figure 4, while the impact of this parameter on the total mass distributions is shown in Figure 6 of Appendix B. Other than the lowest assumed BH budget of 10, imposing a BH budget has no effect on the NG+1G pairings because larger assumed values still exceed the maximum number of BHs needed to fully grow an NG+1G branch. For the NG+ ≤ NG and NG+NG pairings, the impact of imposing a BH budget is most apparent at higher escape velocities. The assumed BH budget has the largest effect on the NG+ ≤ NG pairing because recoil kicks are suppressed relative to the NG+NG pairing, and thus, this constraint acts to suppress mass growth at the highest escape velocities. At an escape velocity of 1000 km s⁻¹, the percentage of systems in the NG+ ≤ NG pairing scenario and the LVC 1G population with total masses greater than 100 M_⊙ drops from 61% for a BH budget of 100 to 48% for a BH budget of 30 and 11% for a BH budget of 10.

Hierarchical BBH mergers are a natural occurrence in dynamical environments, with merger rates strongly dependent on the escape velocity of their host. We demonstrate that a range of models inevitably overproduce high-mass mergers through hierarchical assembly, leading to tension with current observational constraints if such formation environments dominate the BBH merger rate. Using simple models to represent BBH pairing functions and properties of host environments, we explore the retention efficiency and resultant mass spectrum of BBHs in the hierarchical merger paradigm. Regardless of whether host environments preferentially lead to intergenerational (NG+1G and NG+ ≤ NG) or equal-generation (NG+NG) pairings, we find hierarchical mergers in environments with moderate to high escape velocities (∼300–1000 km s⁻¹) will efficiently produce high-mass BBH mergers, with a significant fraction having total source-frame masses ≳100 M_⊙. For environments where intergenerational pairings are preferred, the mass buildup is slower, though the retention fraction eventually flattens out and leads to a runaway merger scenario. For equal-generation pairings, the retention fraction continually drops with each merger generation, but the mass buildup is significantly expedited. Assuming a large budget of BHs available for hierarchical mergers, environments with escape velocities >500 km s⁻¹ result in at least 7%–55% of their hierarchical mergers having source-frame total masses greater than 100 M_⊙.

Depending on the relative number of hierarchical mergers compared to “1G+1G” mergers, such environments therefore exhibit potential incompatibility with the observed BBH mass spectrum due to an overabundance of high-mass mergers, particularly if such environments contribute significantly to the local BBH merger rate. NCs with escape velocities of ≳300 km s⁻¹ are rare in the local universe (Antonini & Rasio 2016) and thus likely have a minor contribution to the observed population of BBHs. Local BBH merger rate predictions from AGN disks span many orders of magnitude due to the many physical uncertainties inherent to this channel (McKernan et al. 2018; Gröbner et al. 2020), with certain studies arguing that mergers from AGN disks make up a significant fraction (>25%) of the detected BBH population (e.g., Ford & McKernan 2021; Gayathri et al. 2021). We note that multichannel analyses of dynamical environments such as Mapelli et al. (2022), which consider cosmologically motivated rate estimates of both “1G+1G” and hierarchical mergers from young star clusters, GCs, and NCs in addition to field binaries, find no overproduction of hierarchical mergers, though the AGN disk scenario is not included in their analysis.

We stress that our analysis does not directly constrain branching fractions from dynamical environments; rather, it provides an estimate of the joint constraints on branching fractions and the relative ratio of “1G+1G” mergers to hierarchical mergers. For example, in environments with escape velocities of ∼1000 km s⁻¹, an NG+1G pairing function and an IMF 1G population, similar to what one might expect for an AGN disk scenario (see, e.g., Yang et al. 2019a; Tagawa et al. 2021), we find 69% of hierarchical mergers to have total masses greater than 100 M_⊙, whereas the population inference results from the LVC find that <1.5% of all mergers have masses greater than 100 M_⊙ at 90% credibility (Abbott et al. 2021c). If one were to assume mergers in AGN disks dominate the production of systems observed by the LVC, this provides a rough estimate that 1G mergers must be at least 46 times more prevalent than hierarchical mergers. Constraints can thus be placed on aspects of AGN environments that influence the relative rate of hierarchical mergers, such as disk lifetimes (Secunda et al. 2019) and how efficiently the orbits of hierarchical merger products decay into the central supermassive BH. Alternatively, the high efficiency of forming high-mass systems through hierarchical mergers in environments with escape velocities ≳300 km s⁻¹ may indicate that these environments are not dominant contributors to the overall population of merging BBHs.

The toy models considered in this paper are approximations of the detailed evolution of BH mergers in dynamically rich environments. They may fall short of capturing important intricacies of hierarchical assembly, especially in environments that are gas rich or involve interactions with a central massive BH. However, the multiple pairing methods we construct broadly capture the diversity of expected hierarchical assembly processes in various host environments. Additionally, we consider a single initial BH mass function for all environments, whereas environments with low escape velocities may lead to a more top-heavy mass spectrum because low-mass BHs may be more readily ejected at formation by supernova kicks (Mapelli et al. 2021). An analysis that self-consistently models the parameter distributions of both 1G BHs and an arbitrary number of higher-generational populations could hold promise (e.g., Doctor et al. 2020; Kimball et al. 2020, 2021; Mould et al. 2022), though expanding such methodologies beyond second-generation hierarchical mergers is nontrivial and is the aim of future work. Nevertheless, studies such as Mould et al. (2022) have made headway in this direction by relying on machine-learning techniques to interpolate between astrophysical models, which they use to extend inference capabilities to account for higher-generational hierarchical mergers.

We note that the formation of IMBHs through hierarchical assembly also requires that the growing BH seeds pass through the sensitive frequency range of ground-based GW detectors (e.g., Fragione et al. 2022). The detection, or nondetection, of mass-gap BHs, as well as BHs beyond the PI mass gap, provide important constraints to IMBH growth mechanisms. Supermassive BH growth may also be due in part to the hierarchical assembly of stellar-mass BH seeds (e.g., Chen et al. 2022), and in this scenario, one would also expect to observe such mergers at high redshifts in the sensitive frequency range of future ground-based GW detectors.

Our work highlights the tension between models that produce binaries in and above the PI mass gap at high efficiency and existing limits on mergers beyond the mass gap. The high efficiencies by which a particular formation channel produces extreme systems may be detrimental to its consistency with the population of GW sources as a whole. Careful consideration of overall population properties and selection effects, as well as the inclusion of multiple potential formation channels, are necessary to contextualize extreme systems with respect to the full population of GW signals. Viable models for the formation of stellar-mass BHs, IMBHs, and supermassive BH seeds may need to populate the PI mass gap while carefully avoiding overpopulating the mass region immediately above the gap. Without care, models that populate the gap can lead to a cluster catastrophe, producing runaway growth of BHs with masses ≳100 M_⊙, in tension with existing observational limits.

We thank Maya Fishbach and Shanika Galaudage for providing code for drawing mock events from population models. We acknowledge Will Farr, Saavik Ford, Giacomo Fragione, Chase Kimball, Kyle Kremer, Michela Mapelli, Barry McKernan, and Carl Rodriguez for useful discussions. We also thank the anonymous referee whose comments significantly improved this manuscript. Support for this work and M.Z. was provided by NASA through the NASA Hubble Fellowship grant HST-HF2-51474.001-A awarded by the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Incorporated, under NASA contract NAS5-26555. D.E.H. is supported by NSF grants PHY-2006645, PHY-2011997, and PHY-2110507, as well as by the Kavli Institute for Cosmological Physics through an endowment from the Kavli Foundation and its founder Fred Kavli. This work was performed in part at the Aspen Center for Physics, which is supported by NSF grant PHY-1607611. This material is based upon work supported by NSF’s LIGO Laboratory which is a major facility fully funded by the National Science Foundation.

Software: Astropy (Robitaille et al. 2013; Price-Whelan et al. 2018); Bilby (Ashton et al. 2019); iPython (Pérez & Granger 2007); Matplotlib (Hunter 2007); NumPy (Oliphant 2006; Van Der Walt et al. 2011); Pandas (McKinney 2010); precession (Gerosa & Kesden 2016); SciPy (Virtanen et al. 2020).

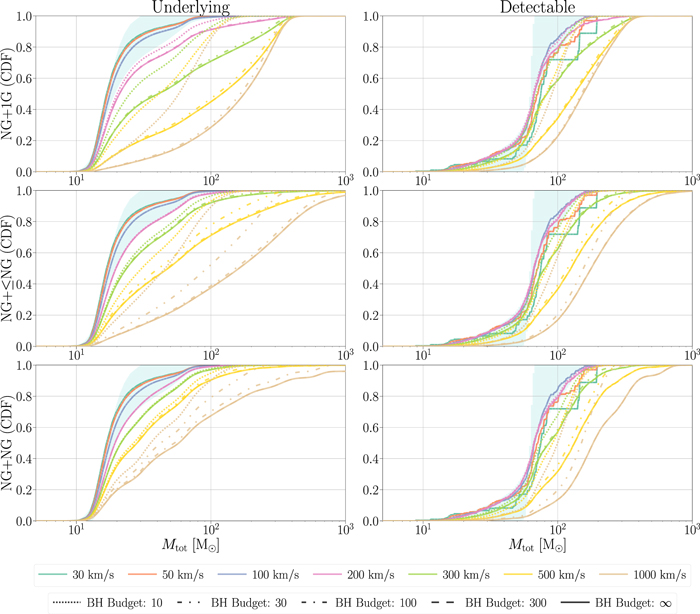
In Section 2.2 we describe the simple model used for initializing a particular merger tree at a given redshift, as well as our assumptions for the delay time between subsequent mergers. The fiducial model we assume for delay times, which is a log-uniform distribution between 10 Myr and 100 Myr, is representative of gas-free environments with relatively short mass segregation timescales. Here, we explore variations in the assumed delay-time distribution, extending our fiducial distribution to log-uniform between Δt = [10 Myr, 1 Gyr], as well as considering a log-uniform between Δt = [100 Myr, 14 Gyr]. Figure 5 shows how these variations affect the underlying and detectable BH mass spectrum of hierarchical mergers across our range of assumed escape velocities.

Zoom In Zoom Out Reset image size

Increasing the assumed delay times to Δt = [10 Myr, 1 Gyr] has a negligible impact on the underlying distribution, as the increase in the number of systems that now merge at times later than the present is minor. This impact is more prominent with the Δt = [100 Myr, 14 Gyr] delay-time model because many more systems now readily merge after the present day (dotted lines in Figure 5). This acts to truncate the mass distribution, as the most massive mergers that have proceeded through the most hierarchical mergers more readily merge at times beyond the present. The detectable distributions in the right-hand column of Figure 5 show more complex behavior. For all pairing scenarios and escape velocities, the extended Δt = [10 Myr, 1 Gyr] delay-time model pushes to larger source-frame total masses in the detectable distribution than the fiducial model. This is due to high-mass systems from numerous chains of hierarchical mergers more readily merging in the local universe and being more accessible to ground-based GW observatories. On the other hand, the longest delay-time model explored (Δt = [100 Myr, 14 Gyr]) truncates the high end of the mass spectrum significantly due to many more systems merging beyond the present day. This is especially apparent in the NG+1G pairing model, as a large quantity of subsequent hierarchical mergers is necessary to significantly build up the mass of the merger product. The influence of large delay times is less apparent in the detectable distributions for near-equal-mass pairings, such as the NG+NG pairing scenario, as it requires a smaller number of repeated mergers to bolster the mass spectrum significantly.

For mass distributions presented in the main text, we assume that the number of BHs the hierarchical merger product can consume is only limited by the maximum number of mergers possible for each pairing scenario as described in Section 2.2. Here, we relax this assumption by imposing a limit on the BH budget available for each hierarchical merger branch. This accounts for all BHs consumed throughout the evolution of the merger product. Figure 6 displays variations in the resultant mass distribution of hierarchical mergers for the LVC 1G population model when differing assumptions for the BH budget are imposed. We note that a more physically realistic approach for implementing the BH budget would depend on the escape velocity of the host environment, which in turn depends on the total mass of the cluster environment. However, in this analysis, we keep these parameters uncorrelated to explore their impact on mass distributions independently.

Zoom In Zoom Out Reset image size