Abstract
We carried out spectroscopic monitoring of 21 low-redshift Seyfert 1 galaxies using the Kast double spectrograph on the 3 m Shane telescope at Lick Observatory from 2016 April to 2017 May. Targeting active galactic nuclei (AGNs) with luminosities of λLλ(5100 Å) ≈ 1044 erg s−1 and predicted Hβ lags of ∼20–30 days or black hole masses of 107–108.5 M⊙, our campaign probes luminosity-dependent trends in broad-line region (BLR) structure and dynamics as well as to improve calibrations for single-epoch estimates of quasar black hole masses. Here we present the first results from the campaign, including Hβ emission-line light curves, integrated Hβ lag times (8–30 days) measured against V-band continuum light curves, velocity-resolved reverberation lags, line widths of the broad Hβ components, and virial black hole mass estimates (107.1–108.1 M⊙). Our results add significantly to the number of existing velocity-resolved lag measurements and reveal a diversity of BLR gas kinematics at moderately high AGN luminosities. AGN continuum luminosity appears not to be correlated with the type of kinematics that its BLR gas may exhibit. Follow-up direct modeling of this data set will elucidate the detailed kinematics and provide robust dynamical black hole masses for several objects in this sample.
Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
It has been known for about two decades that black hole (BH) mass exhibits a tight correlation with the stellar velocity dispersion of the galactic bulge within which it resides, and this relation holds over several orders of magnitude in black hole mass (e.g., Ferrarese & Merritt 2000; Gebhardt et al. 2000). This relation suggests that supermassive black holes and their host galaxies are tightly linked throughout their lifetimes. A fundamental understanding of the growth of supermassive black holes and their interaction with their immediate vicinity will provide key constraints on cosmological models of galaxy evolution (Springel et al. 2005; Croton et al. 2006). A crucial component in these numerical recipes is therefore the accurate determination of black hole masses as a function of cosmic history.
Robust black hole mass measurements have been limited mostly to nearby galaxies owing to the exquisite angular resolution needed to spatially resolve a black hole’s sphere of influence. The technique of temporally resolving the structure of the broad-line region (BLR) around an actively accreting black hole, called reverberation mapping (RM; Blandford & McKee 1982; Peterson 1993), provides a viable alternative—or in the case of the distant universe, the only currently available—tool for directly measuring black hole masses.
Black hole scaling relations, such as that between the BLR size and the active galactic nuclei (AGN) rest-frame luminosity at 5100 Å (the radius–luminosity relationship; Wandel et al. 1999; Kaspi et al. 2000, 2005; Bentz et al. 2006, 2009a, 2013; Shen 2013), enable “single-epoch” mass-determination methods for estimating black hole masses in broad-lined AGNs out to high redshifts. The calibrations for such mass estimates, however, rest upon the presumptions that distant quasars are similar to the low-redshift reverberation-mapped AGNs, while in fact they exhibit higher luminosities and larger Eddington ratios (Richards et al. 2011; Shen 2013). Whether virial assumptions for BLR gas dynamics based on local Seyferts can be extended to distant quasars must be tested against a broad range of black hole masses and luminosities. RM, as a tool that probes BLR gas structure, provides the means for such a test.
The RM method is successful for black hole mass determination because the emission lines in the BLR gas are found to respond to the stochastic continuum variations in an AGN via the transfer function (Peterson 1993)

where L(vz , t) is the emission-line luminosity at the line-of-sight velocity vz at observed time t, C(t) is the continuum light curve, and Ψ(vz , τ) is the transfer function that maps continuum variability to the emission-line response at vz after some time delay τ. This simple model assumes a linear response and no background light; fitting AGN light curves requires the linearized echo model that subtracts off the reference levels, e.g., L(vz , t) − L0(vz ) (see discussion in Horne et al. 2021). Monitoring both the continuum and the emission-line light curves provides data that can allow for the determination of Ψ(vz , τ), also known as the velocity-delay map, whose shape depends on the structure and kinematics of the BLR (Horne et al. 2004). In practice, precise velocity-resolved information in the form of the transfer function demands intense monitoring with frequent sampling, high signal-to-noise ratio (S/N) data, and long duration. As a result, the number of AGNs with such data available to-date has been limited.
With the goal of refining black hole scaling relations through expanding the local reverberation-mapped AGN database by which they are anchored, we embarked on a campaign aimed to monitor AGNs at higher luminosity than samples targeted in the 2008 and 2011 campaigns of the Lick AGN Monitoring Project (LAMP; e.g., Bentz et al. 2009b; Barth et al. 2015). Higher-luminosity AGNs tend to have longer lags. Coupled with the fact that they have weaker variability amplitudes owing to the ample fuel supply in their accretion disks (vanden Berk et al. 2004; Wilhite et al. 2008; MacLeod et al. 2010), lag recovery is more challenging for these objects. The advent of large, multi-object programs such as the Sloan Digital Sky Survey (SDSS)-RM (Shen et al. 2015) and the Australian Dark Energy Survey (OzDES; Yuan et al. 2015) provides a new landscape where large numbers of reverberation lags for Hβ, Mg ii, and C iv in quasars are determined over a broad redshift range (Shen et al. 2016; Grier et al. 2017, 2019). Grier et al. (2017) measured Hβ time lags for 44 AGNs with luminosities log[λ Lλ (5100 Å)/L☉] ≈ 43–45.5 at redshifts z = 0.12–1. Early results from the SDSS-RM campaign determined C iv lags in 52 quasars (Grier et al. 2019), whereas those from OzDES found two C iv-based black hole masses to be among the highest-redshift (z = 1.9–2.6) and highest-mass black holes [MBH = (3.3–4.4) × 109 M☉] measured thus far with RM studies (Hoormann et al. 2019). Complementing these large multifiber spectroscopic studies, our campaign targeted AGNs at low redshifts and aimed to yield high-fidelity data for velocity-resolved lag measurements and dynamical modeling.
During the past several years, different groups have determined resolved velocity-delay reverberation signatures for dozens of unique objects among local Seyferts, changing-look AGNs, and those with Hβ asymmetry (e.g., Bentz et al. 2010a; Grier et al. 2013; Pancoast et al. 2014b; De Rosa et al. 2018; Du et al. 2018a; Williams et al. 2018, 2020; Lu et al. 2019; Zhang et al. 2019; Sergeev 2020; Lu et al. 2021; Bentz et al. 2021). Our primary intent is to use a large, relatively broad sample to investigate statistical luminosity-dependent trends in BLR structure and gas dynamics using velocity-resolved reverberation, which could directly impact the accuracy of virial mass estimates. Here we present our first results that focus on new Hβ velocity-resolved measurements along with integrated Hβ lags and virial black hole masses. Our data set will allow for forward-modeling work using, for instance, the CARAMEL code (Pancoast et al. 2011, 2014a; L. Villafaña et al. 2021, in preparation) to directly determine black hole masses.
This paper is organized as follows. The sample selection is described in Section 2. In Section 3, we present our observational program at Lick Observatory and details of the data reduction and processing work. Section 4 reports on our photometric campaign to provide the continuum light curves for our AGN sources. In Section 5, we illustrate our emission-line light curves and subsequent integrated and velocity-resolved Hβ lag detections, including an assessment of the lag significance and the observed variety of BLR kinematics. Section 6 depicts our line width measurements and derived virial black hole masses, within the larger context of how our results compare with the existing AGN radius–luminosity relation.
Throughout the paper, we have adopted H0 = 67.8 km s−1 Mpc−1, Ωm = 0.308, and Ωvac = 0.692 (Planck Collaboration et al. 2016).
2. Sample Selection
The past LAMP campaigns targeted AGNs with Hβ lags of ∼3–15 days (Bentz et al. 2009b, 2010b; Barth et al. 2015). The chief objective of this campaign is to investigate BLR kinematics of moderate-luminosity AGNs, so we targeted primarily Seyfert 1s with extinction-corrected log[λ Lλ (5100 Å)/L☉] ≈ 43.5–43.9. Based on the radius–luminosity relation (e.g., Bentz et al. 2013), the targeted AGN continuum luminosity range corresponds to an Hβ lag range of 20−30 days. We note, however, that recent results from the super-Eddington accreting massive black holes (SEAMBH; Du et al. 2016, 2018b; Du & Wang 2019) and SDSS-RM (Grier et al. 2017) programs have shown that some AGNs have lags shorter than would be expected from earlier versions of the radius–luminosity relation (Bentz et al. 2013).
We applied this 20–30-day criterion in Hβ lag or equivalently λ Lλ (5100 Å) to various catalogs of Type 1 AGNs (e.g., Boroson & Green 1992; Marziani et al. 2003; Peterson et al. 2004; Vestergaard & Peterson 2006; Bachev et al. 2008; Winter et al. 2010; Shen et al. 2011; Zu et al. 2011; Joshi et al. 2012; Bennert et al. 2015; Sun & Shen 2015). Our selection was further narrowed with a redshift limit at z < 0.08 to ensure that the Hβ and [O iii] lines fall blueward of the cutoff wavelength of the dichroic used in the Kast spectrograph (5500 Å). Sources were selected with decl. δ ≥ −5° and magnitude <17 in the optical V or r bands. We also assessed the short-term variability in previous light curves from the Catalina Real-time Transient Survey (Drake et al. 2009) for all of our candidate sources and selected those with at least 0.1 magnitude of variations. Targets having high-quality velocity-resolved lag measurements from previous RM campaigns were excluded (e.g., Denney et al. 2010; Grier et al. 2012; Du et al. 2014; Wang et al. 2014), as were those no longer featuring broad hydrogen recombination lines in archival Lick optical spectra.
In order to ensure that lags can be measured accurately, we placed a further constraint requiring that the monitoring duration of an AGN, defined as the longest continuous period when the AGN can be observed at airmass <2 during our campaign, be at least three times larger than the expected Hβ lag based on simulations. Given that our initial campaign duration was designed to be 9 months long (which extended to 1 yr later on), this constraint resulted in a sample of 29 objects with duration-to-lag ratio >3. Two sources with slightly shorter Hβ lag estimates (Mrk 315: 13 days; Mrk 704: 16 days) were included to better fill the R.A. range of the sample.
After an initial probationary period of ∼1 month, we discarded eight sources showing low continuum variability amplitude, retaining a sample of 21 objects for ongoing monitoring. This final sample of Seyfert 1s and their properties are listed in Table 1.
Table 1. Sample Properties
| Object | Other Name(s) | R.A. | Decl. | Redshift | Reference |
|---|---|---|---|---|---|
| (J2000) | (J2000) | ||||
| Zw 535-012 | 00:36:20.983 | +45:39:54.08 | 0.04764 | 1 | |
| I Zw 1 | UGC 00545, Mrk 1502, PG 0050+124 | 00:53:34.940 | +12:41:36.20 | 0.05890 | 2 |
| Mrk 1048 | NGC 985, VV 285 | 02:34:37.769 | −08:47:15.44 | 0.04314 | 2 |
| Ark 120 | UGC 03271, Mrk 1095 | 05:16:11.421 | −00:08:59.38 | 0.03271 | 3 |
| Mrk 376 | KUG 0710+457, IRAS 07105+4547 | 07:14:15.070 | +45:41:55.78 | 0.05598 | 3 |
| Mrk 9 | 07:36:56.979 | +58:46:13.43 | 0.03987 | 1,3 | |
| Mrk 704 | CGCG 091-065, MCG +03-24-043 | 09:18:26.005 | +16:18:19.22 | 0.02923 | 4 |
| MCG +04−22−042 | 09:23:43.003 | +22:54:32.64 | 0.03235 | 5 | |
| Mrk 110 | PG 0921+525 | 09:25:12.870 | +52:17:10.52 | 0.03529 | 6,7 |
| RBS 1303 | CGS R14.01 | 13:41:12.904 | −14:38:40.58 | 0.04179 | 4 |
| Mrk 684 | 14:31:04.783 | +28:17:14.11 | 0.04608 | 1 | |
| Mrk 841 | J15040+1026 | 15:04:01.201 | +10:26:16.15 | 0.03642 | 5 |
| Mrk 1392 | 1505+0342 | 15:05:56.553 | +03:42:26.32 | 0.03614 | 8 |
| SBS 1518+593 | 15:19:21.650 | +59:08:23.70 | 0.07810 | 9 | |
| 3C 382 | CGCG 173-014 | 18:35:03.390 | +32:41:46.80 | 0.05787 | 2 |
| NPM1G+27.0587 | 2MASX J18530389+2750275 | 18:53:03.874 | +27:50:27.72 | 0.06200 | 10 |
| RXJ 2044.0+2833 | 20:44:04.500 | +28:33:12.10 | 0.05000 | 10 | |
| PG 2209+184 | II Zw 171 | 22:11:53.889 | +18:41:49.86 | 0.07000 | 2 |
| PG 2214+139 | Mrk 304 | 22:17:12.262 | +14:14:20.89 | 0.06576 | 2 |
| RBS 1917 | 2MASX J22563642+0525167 | 22:56:36.500 | +05:25:17.20 | 0.06600 | 2 |
| Mrk 315 | 23:04:02.622 | +22:37:27.53 | 0.03887 | 1 |
Note. Objects in this and subsequent tables and figures are listed in R.A. order. Redshifts are from NASA/IPAC Extragalactic Database (NED). References for λ Lλ (5100 Å) used to estimate the Hβ lag in our sample selection: (1) Previous Lick spectra; (2) Marziani et al. (2003); (3) Joshi et al. (2012); (4) Barth et al. (2015); (5) Winter et al. (2010); (6) Peterson et al. (2004); (7) Zu et al. (2011); (8) Bennert et al. (2015); (9) Sun & Shen (2015); (10) Bachev et al. (2008).
Download table as: ASCIITypeset image
3. The Spectroscopic Campaign at Lick
3.1. Overview of the Observational Program
We conducted a spectroscopic monitoring program of 1 yr duration at Lick Observatory on Mount Hamilton, California. Prior to the start of the campaign, we ran simulations to determine the minimum threshold for successful lag recovery among monitoring periods of varying lengths and cadences. Our estimated Hβ lag range required a sampling cadence of two nights per week over the course of 1 yr to sufficiently resolve time-dependent emission-line variations and to extend the temporal baseline for detecting a robust reverberation signal across the entire extent of the BLR, accounting for anticipated weather losses and seasonal gaps.
This project was allocated 100 nights at the Lick 3 m Shane telescope across three observing semesters between 2016 April 28 and 2017 May 6 (UT). The observing runs were distributed mostly with a frequency of ∼2 nights per week as requested, with the exception of bright time and occasional scheduling constraints owing to other time-sensitive observing programs. Partial nights were occasionally exchanged with or obtained from other programs to facilitate the sampling cadence of certain targets during this monitoring period.
Spectroscopic data were taken using the Kast Double Spectrograph (Miller & Stone 1994). The red CCD detector was upgraded halfway into our campaign (2016 September 17–20). The upgrade from the Reticon 400 × 1200 pixel CCD to the Hamamatsu 4096 × 1024 pixel CCD significantly improved the quantum efficiency, up to a factor of two at the red end, and removed severe fringing effects. Images taken with the new red CCD suffered from a high incidence rate of cosmic-ray hits and alpha-particle hits due to radioactive material in the new dewar window. These defects were removed at the reduction stage where frames were combined before the spectrum was extracted.
We employed the following setup for our AGN observations: the D55 dichroic with the 600/4310 grism (nominal coverage of 3300–5520 Å at 1.02 Åpixel−1) on the blue side and the 600/7500 grating (nominal coverage of 4000–11000 Å at 2.35 Åpixel−1 pre-upgrade, and 3800–10000 Å at 1.31 Åpixel−1 post-upgrade) on the red side, a compromise between broad spectral coverage and moderate spectral resolution. The plate scale was 043/pixel for both the blue and the new red detectors, and 0
78/pixel for the old red detector. A slit width of 4″was employed to minimize slit losses due to seeing variations between different nights (Filippenko 1982). A fixed position angle (PA), optimized for each individual target, was chosen so that the spectroscopic aperture sampled the same portion of the host galaxy across the duration of the monitoring campaign.
Exposure times were typically up to 30 min per object each night, split into two or three separate exposures (pre- and post-upgrade of the red CCD, respectively) to facilitate cosmic-ray cleaning. Standard calibrations including bias exposures, arc frames (using the Ar, He, Hg, Cd, and Ne lamps), and dome flats were taken during the afternoon, and well-calibrated flux standard stars (G191B2B, Feige 34, BD+284211, HZ44, BD+262606, and/or BD+174708) were observed during the nights. Before the red CCD upgrade, red-side observations suffered from severe fringing at wavelengths longward of 7000 Å. In order to remove the fringe pattern, dome flats at the position of every object were taken before or after each standard star and AGN observation on the red side. This time-consuming procedure was no longer needed after the upgrade that eliminated the fringing effect. The observing parameters for our sample are listed in Table 2.
Table 2. Observing Parameters
| Object | Slit PA |
| Monitoring Period | Nobs | S/N | Nphot |
|---|---|---|---|---|---|---|
| (deg) | (s) | (UT) | ||||
| Zw 535−012 | 100 | 1800 | 2016/06/27−2017/03/04 | 41 | 57 | 10 |
| I Zw 1 | 45 | 1600 | 2016/07/03−2017/02/01 | 34 | 103 | 6 |
| Mrk 1048 | 0 | 1800 | 2016/08/08−2017/02/16 | 27 | 88 | 5 |
| Ark 120 | 0 | 1800 | 2016/08/15−2017/03/26 | 34 | 124 | 5 |
| Mrk 376 | 70 | 1800 | 2016/05/01−2017/05/01 | 31 | 84 | 6 |
| Mrk 9 | 90 | 1800 | 2016/05/01−2017/05/01 | 33 | 78 | 5 |
| Mrk 704 | 130 | 1800 | 2016/10/20−2017/05/01 | 23 | 106 | 3 |
| MCG +04−22−042 | 145 | 1800 | 2016/05/01−2017/05/01 | 34 | 54 | 7 |
| Mrk 110 | 44 | 1200 | 2016/05/01−2017/05/01 | 41 | 74 | 6 |
| RBS 1303 | 20 | 1200 | 2016/05/01−2017/05/01 | 22 | 67 | 5 |
| Mrk 684 | 60 | 1800 | 2016/05/01−2017/05/01 | 43 | 98 | 12 |
| Mrk 841 | 50 | 800 | 2016/05/01−2017/05/01 | 45 | 77 | 11 |
| Mrk 1392 | 50 | 1800 | 2016/05/01−2017/05/01 | 39 | 55 | 10 |
| SBS 1518+593 | 90 | 1800 | 2016/05/01−2017/05/01 | 48 | 44 | 8 |
| 3C 382 | 70 | 1800 | 2016/05/01−2016/12/03 | 50 | 81 | 12 |
| NPM1G+27.0587 | 60 | 1800 | 2016/05/01−2016/12/03 | 38 | 55 | 7 |
| RXJ 2044.0+2833 | 60 | 1800 | 2016/05/01−2016/12/31 | 46 | 58 | 9 |
| PG 2209+184 | 60 | 1800 | 2016/05/01−2016/12/31 | 40 | 32 | 9 |
| PG 2214+139 | 60 | 1800 | 2016/05/18−2016/12/31 | 43 | 81 | 10 |
| RBS 1917 | 30 | 1800 | 2016/06/01−2016/12/31 | 32 | 39 | 9 |
| Mrk 315 | 60 | 1800 | 2016/06/07−2016/12/31 | 35 | 59 | 9 |
Note.
 represents the typical total on-source exposure time for each AGN every night it was observed, usually split among 2–4 frames. Nobs represents the total number of spectroscopic observations for each source. S/N represents the median S/N per pixel in the continuum at (5100–5200)(1 + z)Å. Nphot represents the number of photometric nights for each source.
represents the typical total on-source exposure time for each AGN every night it was observed, usually split among 2–4 frames. Nobs represents the total number of spectroscopic observations for each source. S/N represents the median S/N per pixel in the continuum at (5100–5200)(1 + z)Å. Nphot represents the number of photometric nights for each source.
Download table as: ASCIITypeset image
The wet 2016–2017 winter season at Lick hampered our observing effort, particularly during December through February. Overall, our spectroscopic campaign achieved an observational success rate of ≲70%, where 30 nights were lost entirely to weather or dome issues. For another 12 nights, only six or fewer AGNs were observed when typically 12–15 objects would have been observed on a night with good conditions. We were confident that at least 14 nights of observations were carried out under photometric conditions. Of the 70 nights when data were obtained, half were done with the old red CCD and half with the upgraded detector. The number of total epochs observed for each object ranges from 22 to 50, with a median of 38 (see Table 2).
3.2. Spectroscopic Data Reduction
The Kast spectroscopic data were reduced using a combination of standard routines in IRAF and IDL, following the procedure outlined by Barth et al. (2015). Here we provide a brief description of the reduction process of the blue-side data and pre-/post-upgrade red-side data.
In general, the data were processed via bias subtraction, flat-fielding, cosmic-ray cleaning, one-dimensional extraction using an unweighted boxcar extraction region, wavelength calibration, and flux calibration. Error spectra were extracted and propagated through all subsequent calibration steps. Multiple spectra taken on the same night were combined. The width adopted for the spectral extraction was 10″, though it was widened to ∼15″–20″ for some sources (Mrk 315, Mrk 9, MCG +04−22−042, and NPM1G+27.0587) and during particular nights where the seeing was exceptionally poor.
Most of the AGNs were flux calibrated using the standard-star exposure that was closest in airmass. However, the flux-calibrated spectra for a few epochs exhibited some abnormal slopes and features close to the dichroic cutoff. We were unable to conclusively determine the cause of these anomalies, but they were most likely related to the dichroic. Since the [O iii] λ5007 line, situated close to the dichroic cutoff, was assumed to be constant throughout the observing campaign and was used to normalize the nightly spectra, this peculiarity identified in several spectra added extra scatter to the Hβ light curves. In these cases, we attempted to correct the problem by calibrating the AGNs with standard stars that were taken close in time for six nights. As a result, this flux-calibration issue was partially rectified but remained responsible for some residual scatter in the emission-line light curves. For eight sources (Ark 120, RBS 1303, Mrk 9, RXJ 2044.0+2833, Zw 535−012, SBS 1518+593, Mrk 684, and Mrk 110), we further divided the [O iii] light curve by the median [O iii] flux, and subsequently normalized the Hβ light curve with the residual [O iii] light curve. This normalization helped to mitigate the residual scatter remaining in the Hβ light curves. We suspect that this flux-calibration anomaly due to the dichroic was occurring at a lower level throughout much of the campaign, which caused scatter larger than what might be typically achievable in other RM data sets.
For red-side data taken prior to 2016 September 20, each observation was flattened using a dome-flat exposure taken at the same telescope position. For red-side data taken between 2016 September 20 and 2017 January 31, the Kast red dewar was slightly tilted, and thus the two-dimensional spectra had to be adjusted with a rotation of 0.9° before spectral extraction.
3.3. Photometric and Spectral Scaling
To ensure that all of the spectra for each AGN are on consistent flux and wavelength scales across the monitoring period, a modified version of the procedure described by van Groningen & Wanders (1992, hereafter VGW92) was applied to the blue-side data for internal calibration (see Barth et al. 2015; Fausnaugh 2017, for more details). Having the spectra exhibit consistent spectral resolution throughout the temporal series is important particularly for extracting velocity-resolved measurements. First, we computed the shifts in wavelength among the time-series spectra from cross-correlation. We applied these shifts to align the spectra and calculated an initial mean spectrum that was then designated as the reference. The [O iii] λ5007 fluxes, presumed to be intrinsically constant throughout the course of the observing campaign, were measured from spectra taken during photometric nights and were averaged to estimate the true absolute flux of [O iii]. The number of photometric nights designated per object ranged from three to 12, with a median of eight nights. The resulting reference spectrum was then scaled to match this measurement of the [O iii] flux, with a median uncertainty of 8%.
Each night’s spectrum was then aligned and scaled to the reference by matching the [O iii] λ5007 emission-line profile following our modified VGW92 scaling method. In order to minimize variations outside of intrinsic AGN variability, we aimed to achieve a uniform spectral resolution across the full time series of spectra. Where VGW92 ignores resolution corrections for epochs observed at lower resolution than the reference spectrum, we adopted instead a modified approach similar to that described by Fausnaugh (2017). We first applied a Gaussian broadening kernel to the reference spectrum to ensure that all of the rescaled spectra match a single resolution, typically the worst among the spectra. Excluding the occasional extreme outliers, this broadening kernel had a typical σ of ∼1.5–3 Å with a median σ of 2 Å for each AGN. Each of the spectra was then aligned by wavelength, scaled in flux, and broadened in spectral resolution to match the [O iii] line profile of the broadened reference spectrum.
We performed a comparison of the modified VGW92 spectral scaling method to that using the Python code mapspec (Fausnaugh 2017) with the same wavelength windows and broadened reference spectrum. Differences between the two approaches include the following: (i) VGW92 calls for using a Gaussian kernel for smoothing, while mapspec offers an additional option of using Gauss-Hermite polynomials; and (ii) our modified VGW92 approach fits for free parameters via χ2 minimization, while mapspec uses a Bayesian framework to optimize rescaling parameters and estimate model uncertainties. The runtime for the modified VGW92 method was typically ∼100 times shorter than for mapspec. We ran several tests comparing the level of scatter in the light curves of the [O iii] line that resulted from both methods and concluded that modified VGW92 performed better for most of the AGNs in our sample. We subsequently adopted the spectra scaled with the modified VGW92 approach for the ensuing analysis.
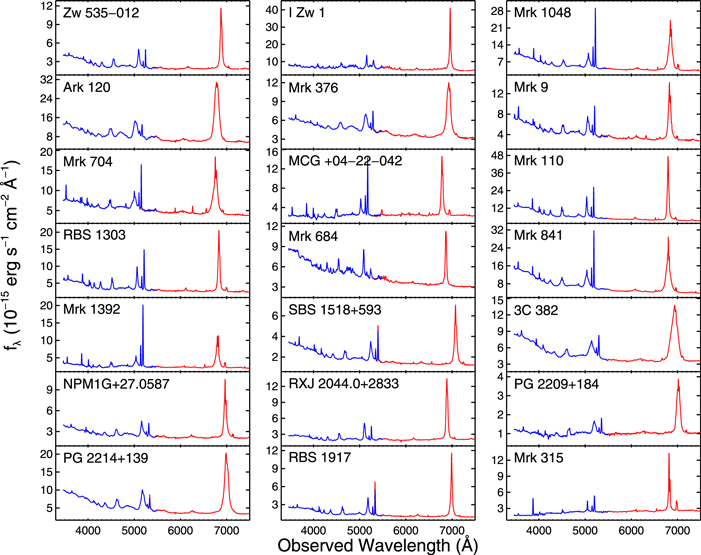
The scaling of the red-side data took a different approach. To normalize the red-side flux scale, red-side spectra were stitched to the corresponding blue-side spectra via aligning their overlapping regions (∼5300–5500 Å). All spectra were first aligned to the reference spectrum in wavelength. Because the ends of the spectra tended to be noisy, we used a weighted average to determine the overall multiplicative scaling factor. This technique worked well in most cases where the spectra were smooth or well behaved at the ends. The average scaled spectra for the sample are presented in Figure 1.
Figure 1. Mean spectra for the LAMP2016 sample including both blue- and red-side data. Here, as in Table 1, the AGNs are shown in order of increasing right ascensions.
Download figure:
Standard image High-resolution image3.4. Noise-corrected RMS Spectra
Relative variability across the spectrum can be visualized using the rms spectrum. The Peterson et al. (2004) procedure of taking the standard deviation of flux values at each wavelength element over all of the epochs may inadvertently bias the rms spectrum given the inclusion of various noise factors in addition to genuine AGN variability (Barth et al. 2015). To remove the contribution due to photon-counting noise from the rms spectrum, Pei et al. (2017) suggested an approach to produce the “excess rms” (e-rms hereafter) spectrum defined per wavelength element λ and epoch i as
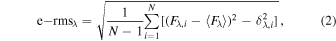
where N is the number of epochs in the time series, 〈Fλ 〉 is the flux averaged over the time series, and Fλ,i and δλ,i refer to the flux and rms uncertainty in the flux at each λ and i, respectively. This was applied to the set of scaled spectra for each AGN.
In the case of an AGN with strongly varying broad-line profiles, broad features are expected to dominate the e-rms spectra in the relevant spectral regions. The narrow [O iii] lines, on the other hand, generally vanish in the rms given that they are assumed to be constant within the time-series data. Presented in Figure 2, the e-rms spectra generally feature a strong blue continuum (except for Mrk 315), broad-line emission in the Balmer series, and (usually) in He ii. The absence of residual narrow [O iii] features confirms that our internal flux calibration worked well near this wavelength, but other residual narrow-line features are likely artifacts of imperfect flux-calibration errors that increase at bluer wavelengths. This is particularly the case for Mrk 315, which has a red e-rms continuum slope and prominent [O ii] λ3727.
Figure 2. The blue-side e-rms spectra for the VGW92-scaled time-series data featuring strong blue continuum and broad-line emission in the Balmer series, overlaid with dashed lines indicating the wavelengths of the prominent emission features (labeled in the top panels). The absence of residual narrow [O iii] features demonstrates the effectiveness of our internal flux calibration at the red end, but other residual narrow-line features (such as the [O ii] λ3727 feature in Mrk 315) are most likely due to a combination of underlying continuum variability and imperfect spectrophotometric calibration errors at the blue end.
Download figure:
Standard image High-resolution image3.5. Spectral Decomposition
The traditional approach of measuring broad emission-line fluxes using a simple linear continuum subtraction is subject to several inadequacies. A linear continuum model is unable to separate blended emission-line features, such as He ii or Fe ii lines that often overlap the broad Hβ profile. Furthermore, a linear fit is a poor approximation to the actual continuum, which includes both AGNs and host-galaxy components. Residual errors from continuum subtraction can be particularly problematic for velocity-resolved RM in the faint high-velocity wings of broad emission lines, where oversubtraction or undersubtraction of the continuum could lead to biased inferences on BLR structure and kinematics. In recent years, spectral decomposition approaches have been applied to the data from some RM campaigns (e.g., Barth et al. 2013, 2015; Hu et al. 2015). By fitting a multicomponent model to each night’s spectrum, the contributions of individual line and continuum components can be better isolated. We find that in most of our objects, the Hβ line profiles isolated using the two methods do not differ dramatically except in the red wings, but spectral decomposition is useful for separating blended line components and removes the starlight component for objects with high starlight fraction much more effectively.
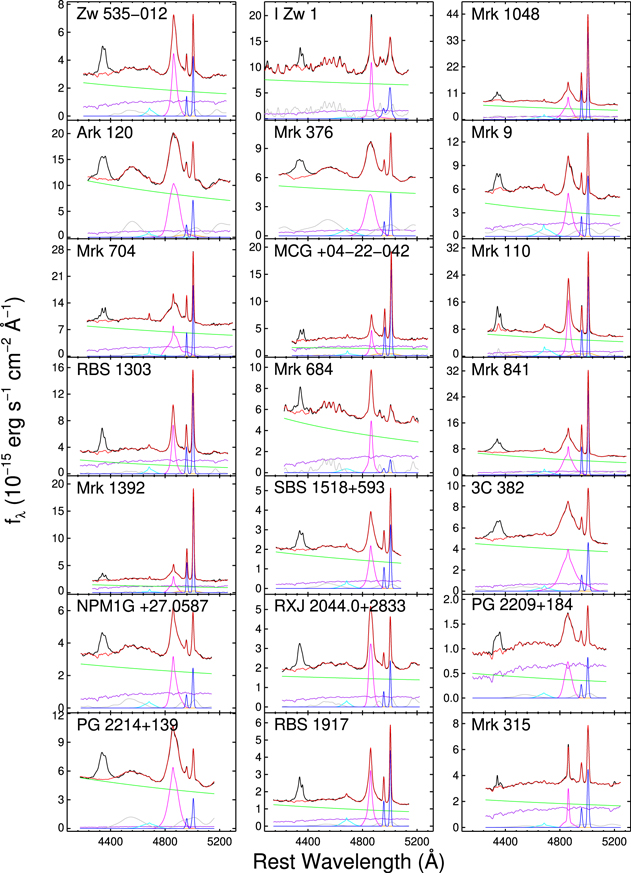
Here we have adopted and applied the spectral fitting method described by Barth et al. (2015) for the Hβ spectral region. We refer the reader to Barth et al. (2015) for a detailed description, and provide a brief overview of the method here. The model components include a power-law AGN continuum, starlight from a single-burst old stellar population at solar metallicity (Bruzual & Charlot 2003) convolved with a Gaussian velocity broadening, and emission lines including [O iii] (narrow), Hβ (broad and narrow), He ii (broad and narrow), He i (broad), and an Fe ii emission template convolved with a Gaussian velocity broadening. Emission-line profiles were modeled using a fourth-order Gauss-Hermite function, except for the He i and He ii lines for which a Gaussian was used. Each line’s velocity centroid was allowed to vary independently, except for the [O iii] λ λ 4959, 5007 lines which were required to have the same velocity profile and a 1:3 flux ratio. For the Fe ii blends, we tested different template spectra as described by Boroson & Green (1992), Véron-Cetty et al. (2004), and Kovačević et al. (2010). In the near future, we will employ a promising, new Fe ii template spectrum based on Mrk 493 (Park et al. 2021). Similar to Barth et al. (2015), the multicomponent Kovačević et al. (2010) template provided the best fit to the Fe ii lines in all of our AGNs and was used for the final fits, except for the case of I Zw 1. For I Zw 1, we found that the Boroson & Green (1992) template, which is based on I Zw 1 itself, provided the best fit with minimized residuals. As part of the fitting process, a Cardelli et al. (1989) reddening model is applied to the model spectrum, allowing E(B − V) to be a free parameter. Fitting was carried out over a rest-wavelength range of approximately 4200–5200 Å, with the exact range tailored to the data for each AGN depending on its redshift. The Hγ + [O iii] λ4363 blend was masked out from the fit, because decomposing this blend would add several additional free parameters to the model. The full model, including the multicomponent Kovačević et al. (2010) iron template, includes 33 free parameters. Model fits were optimized using a Levenberg–Marquart algorithm as implemented by Markwardt (2009). For each AGN, the model was first fitted to the mean spectrum, and the fit parameters from the mean spectral fit were used as the starting parameter estimates for the fit to each individual night’s spectrum. The overall mean spectrum as fitted with the different model components for each galaxy is illustrated in Figure 3.
Figure 3. Spectral decomposition results. The observed mean spectrum (black) for each galaxy is plotted alongside the decomposed model components: starlight (purple), AGN power-law continuum (green), Hβ (magenta), He ii (cyan), He i (orange), Fe ii (gray), and [O iii] (blue). The sum of the fits is represented by the red line. The He i component is negligible in most cases. The blend of Hγ and [O iii] λ4363 is excluded from the fit. The Kovačević et al. (2010) Fe ii template was applied to all sources except for I Zw 1, which was fitted with the Boroson & Green (1992) template.
Download figure:
Standard image High-resolution image4. The Photometric Campaign
AGN continuum light curves were measured from imaging data. We chose the V band since it provides a fairly clean continuum measurement with relatively little contamination from broad emission lines for low-redshift sources. To maximize the chances of detecting the delayed response of the emission-line variations to those of the continuum, we began the photometric monitoring campaign two months before the start of the spectroscopic program. From 2016 February to 2017 May, our team used a network of eight telescopes across the world and obtained high-fidelity V-band images with up to nightly cadence within each object’s monitoring season.
4.1. Telescopes and Cameras
Our photometric campaign included observations with the following telescopes: the 0.76 m Katzman Automatic Imaging Telescope (KAIT; Filippenko et al. 2001) and the Anna Nickel telescope at Lick Observatory on Mount Hamilton, California; the Las Cumbres Observatories Global Telescope (LCOGT) network (Brown et al. 2013; Boroson et al. 2014); the 2 m Liverpool Telescope at the Observatorio del Roque de Los Muchachos on the Canary island of La Palma, Spain (Steele et al. 2004); the 1 m Illinois Telescope at Mount Laguna Observatory (MLO; Smith & Nelson 1969) in the Laguna Mountains, California; the San Pedro Mártir Observatory (SPM) 1.5 m Johnson telescope (Butler et al. 2012; Watson et al. 2012) at the Observatory Astronómico Nacional located in Baja California, México; the Fred Lawrence Whipple Observatory 1.2 m telescope on Mount Hopkins, Arizona; and the 0.9 m West Mountain Observatory (WMO) telescope at Utah Lake in Utah. KAIT, LCOGT, SPM-1.5 m, and Liverpool are fully robotic telescopes. Table 3 summarizes the telescope and detector properties.
Table 3. Telescope and CCD Properties for Imaging Observations
| Telescope | Dmirror | Detector | Field of View | Pixel Scale | Gain | Read Noise | Binning |
|---|---|---|---|---|---|---|---|
| (m) | (″/pix) | (e−/ADU) | (e−) | ||||
| FLWO-1.2 m | 1.2 | Fairchild CCD 486 | 23 | 0.336 | 4.45 | 7.18 | 2 × 2 |
| KAIT | 0.76 | Apogee AP7 | 6 | 0.80 | 4.5 | 12.0 | 1 × 1 |
| LCOGT-2 m | 2.0 | Merope | 4 | 0.467 | 1.0 | 9.0 | 2 × 2 |
| LCOGT-1 m | 1.0 | Fairchild Imaging | 26 | 0.389 | 1.0 | 13.5 | 1 × 1 |
| Liverpool | 2.0 | e2V CCD 231 | 10′×10′ | 0.304 | 1.62 | 8.0 | 2 × 2 |
| MLO-1 m | 1.0 | Fairchild 446 | 13 | 0.718 | 2.13 | 3.88 | 1 × 1 |
| Nickel | 1.0 | Loral | 6 | 0.368 | 1.7 | 8.3 | 2 × 2 |
| SPM-1.5 m | 1.5 | Fairchild 3041 | 5 | 0.32 | 4.2 | 14.0 | 2 × 2 |
| WMO-0.9 m | 0.9 | Finger Lakes PL-09000 | 25 | 0.61 | 1.37 | 12.0 | 1 × 1 |
Download table as: ASCIITypeset image
4.2. Photometry Measurements and Continuum Light Curves
All images were processed with reduction procedures applied as part of the standard pipeline for each facility, including overscan subtraction and flat-fielding. For telescopes that did not include world coordinate system (WCS) solutions as part of their standard processing, we used astrometry.net (Lang et al. 2010) to add WCS information to the FITS headers.
Measurement of the AGN light curves was carried out using the automated aperture-photometry pipeline described by Pei et al. (2014), which can be used to measure AGN light curves using data from any number of telescopes with diverse camera properties. This procedure, written in IDL and based on the photometry routines in the IDL Astronomy User’s Library (Landsman 1993), is designed to automate the process of identifying the AGN and a set of comparison stars in each image by their coordinates, measuring their instrumental magnitudes, and using the comparison-star measurements to obtain a consistent magnitude scale across the full time series for data from multiple telescopes.
The aperture-photometry routine returns photometric uncertainties (in magnitudes) based on the photon-counting statistics, background uncertainty, and CCD readout noise. However, other error sources contribute to the actual error budget, such as imperfect flat-fielding and point-spread function variations across the field of view. To account for these additional error sources, we measured the excess variance 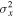 in the light curves of the comparison stars for each AGN, for each telescope’s data. Assuming that the excess variance in the comparison-star light curves is a good estimate of the additional error over and above the statistical uncertainties, we inflated the fractional flux uncertainties on the AGN photometry by addition in quadrature using
in the light curves of the comparison stars for each AGN, for each telescope’s data. Assuming that the excess variance in the comparison-star light curves is a good estimate of the additional error over and above the statistical uncertainties, we inflated the fractional flux uncertainties on the AGN photometry by addition in quadrature using 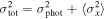 , where σphot is the original photometric uncertainty on a given data point, and
, where σphot is the original photometric uncertainty on a given data point, and 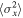 is the average (over all comparison stars in the field) of the excess variance in the comparison-star light curves. This error adjustment was carried out separately for each telescope’s data.
is the average (over all comparison stars in the field) of the excess variance in the comparison-star light curves. This error adjustment was carried out separately for each telescope’s data.
AGN light curves measured from different telescopes tend to have small offsets in magnitude relative to one another as a result of differences in filter transmission curves, even after normalizing them to the same set of comparison stars. To correct for these offsets, we applied an additive shift (in magnitudes) to bring each telescope’s data into best average agreement with the data from the telescope having the most data points for each AGN. Finally, the V-band magnitude scale for each AGN field was calibrated using observations of standard stars taken on photometric nights at WMO and cross-checked against the AAVSO Photometric All-Sky Survey (Henden et al. 2016).
Magnitudes were converted to fλ for measurement of broad emission-line lags. The typical uncertainties of the photometric data points 〈δf 〉 are at the 0.4% level, not exceeding 0.7% for any AGN. The final V-band light curves are presented in Table 4 and shown alongside the emission-line light curves in Section 5.
Table 4. V-band Light-curve Data
| Object | HJD | fλ | δf | Telescope |
|---|---|---|---|---|
| IZw1 | 7555.8493 | 7.124 | 0.020 | LCOGT-fl |
| IZw1 | 7557.8446 | 7.197 | 0.022 | LCOGT-fl |
| IZw1 | 7558.8839 | 7.210 | 0.023 | LCOGT-fl |
| IZw1 | 7559.8607 | 7.207 | 0.022 | LCOGT-fl |
| IZw1 | 7561.9280 | 7.195 | 0.021 | LCOGT-fl |
| IZw1 | 7563.9231 | 7.312 | 0.021 | LCOGT-fl |
| IZw1 | 7564.9379 | 7.237 | 0.018 | LCOGT-McDonald |
| IZw1 | 7566.9208 | 7.226 | 0.021 | LCOGT-fl |
| IZw1 | 7567.9343 | 7.194 | 0.022 | LCOGT-fl |
| IZw1 | 7570.9122 | 7.242 | 0.017 | LCOGT-McDonald |
Note. Dates are listed as HJD−2450000. Units for continuum flux density fλ are 10−15 erg s−1 cm−2 Å−1.
Only a portion of this table is shown here to demonstrate its form and content. A machine-readable version of the full table is available.
Download table as: DataTypeset image
5. Emission-line Light Curves and Lag Determination
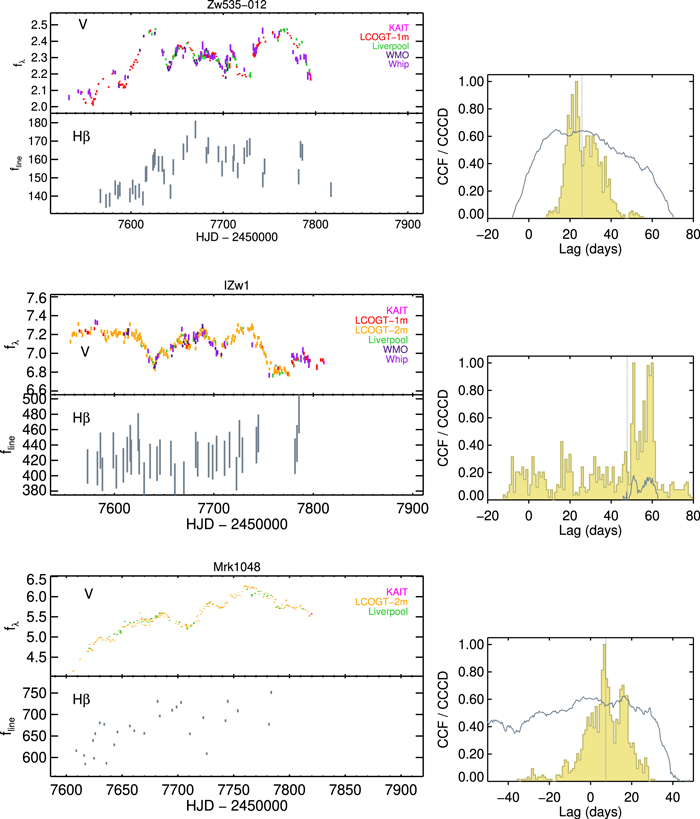
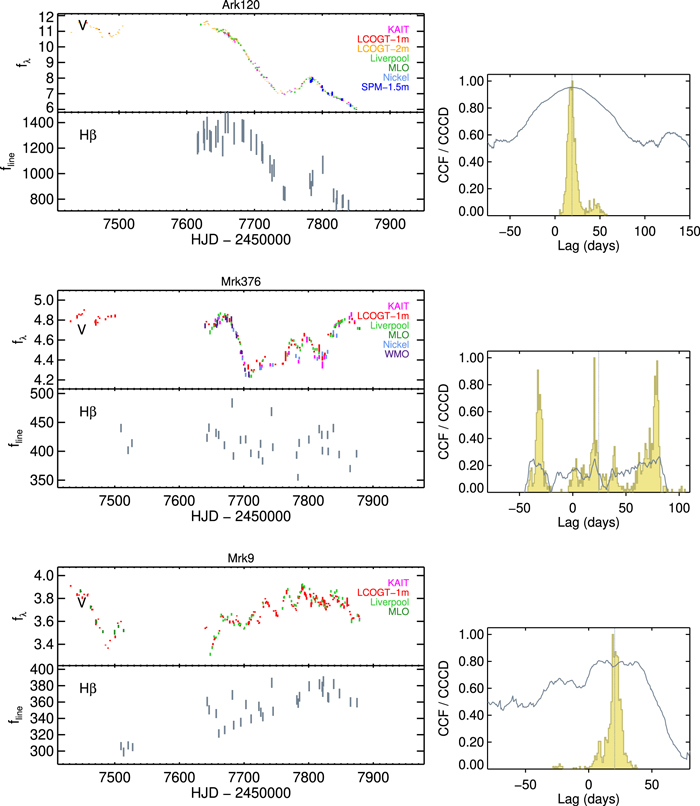
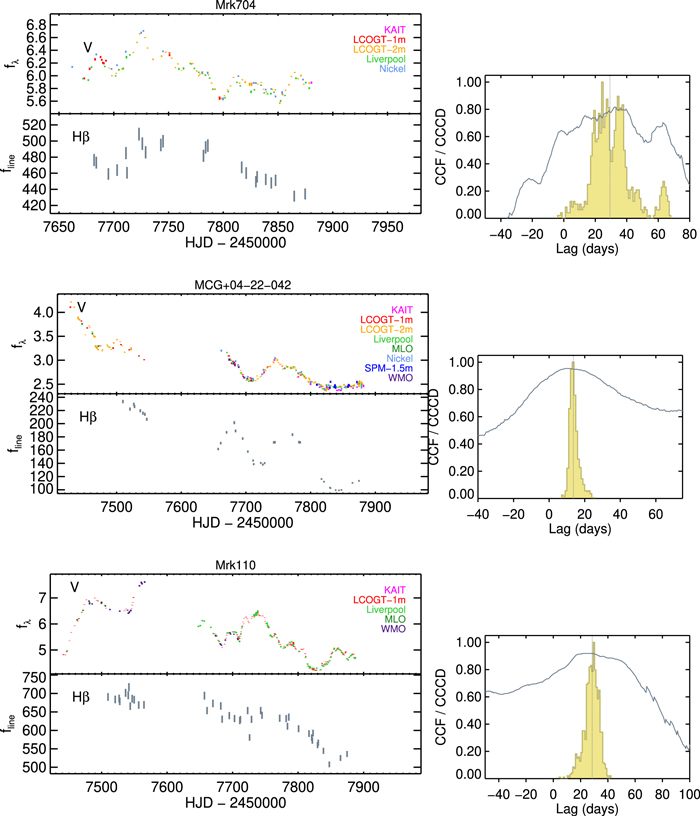
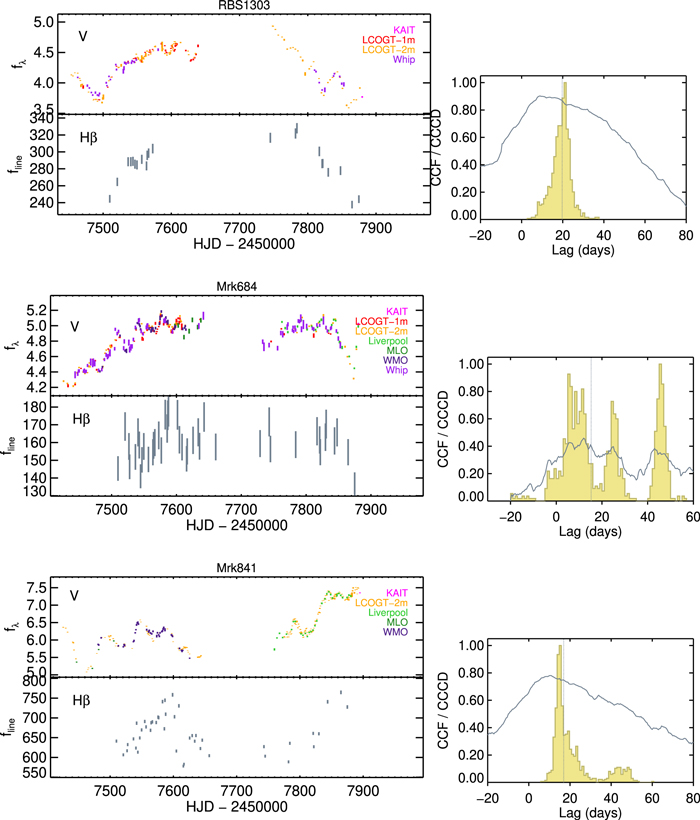
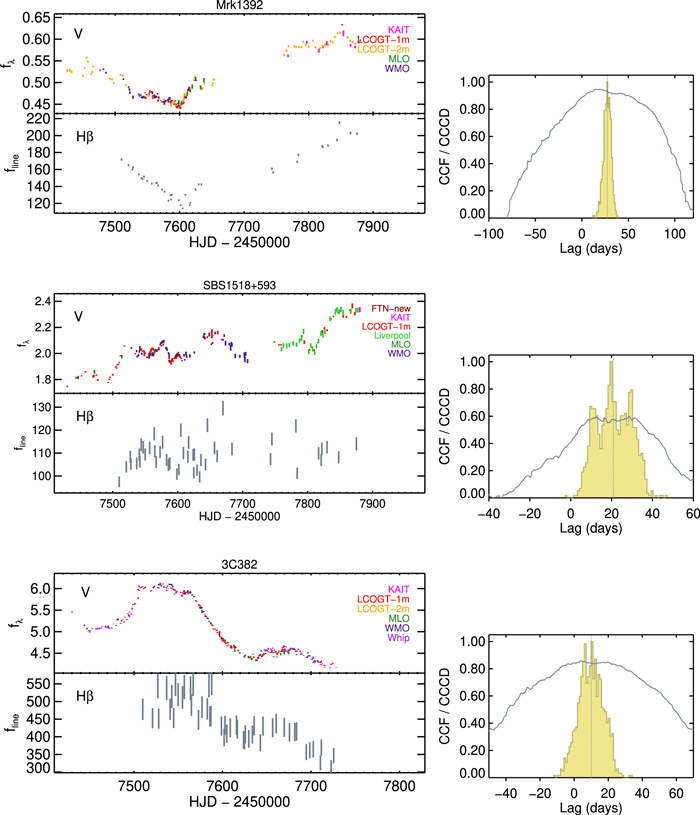
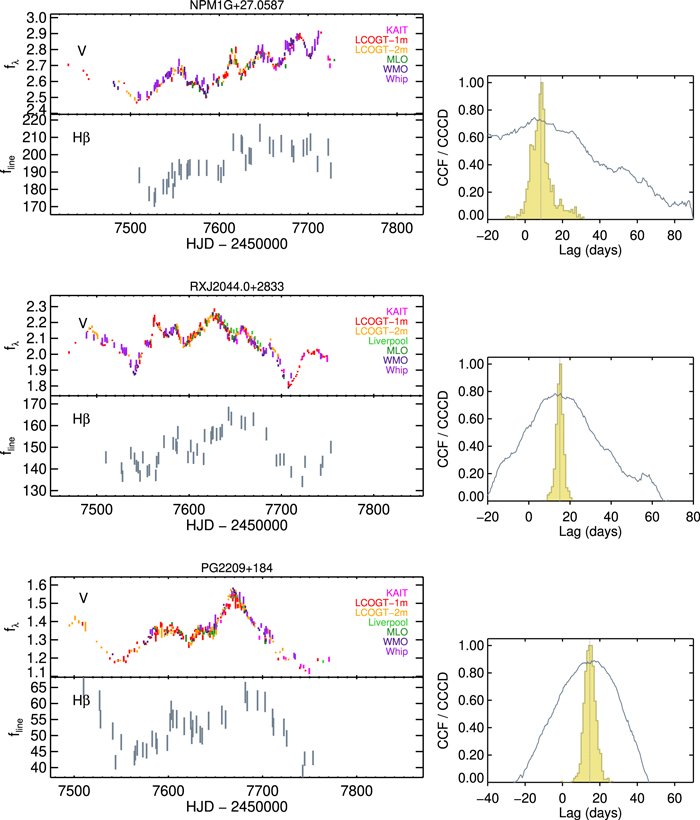
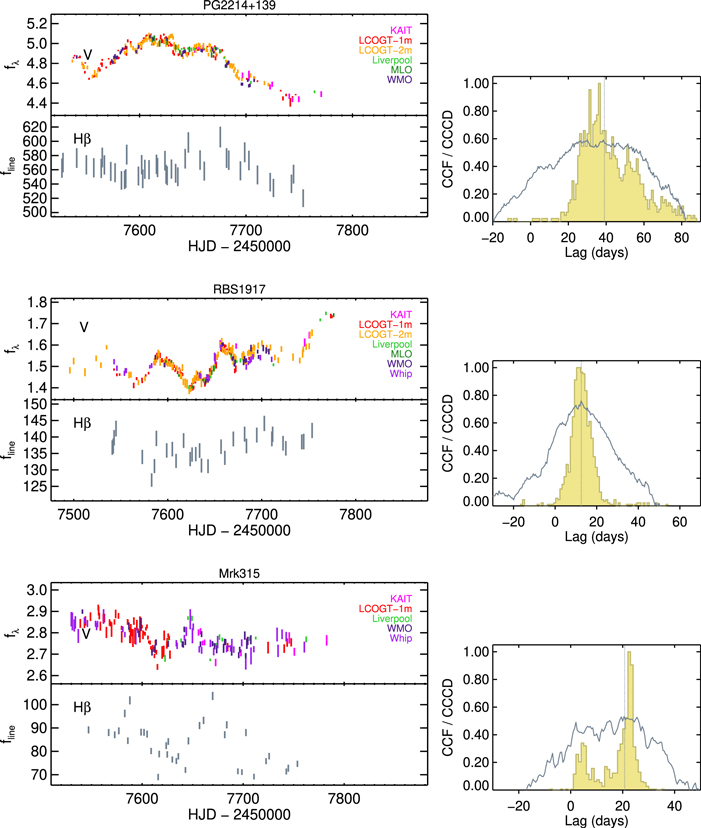
We used results from spectral decomposition to derive Hβ emission-line light curves. The flexibility of the multicomponent modeling afforded us a number of ways to extract the Hβ flux. In the spectral region near the Hβ line, sources with strong Fe ii emission were subjected to substantial degeneracy of spectral decomposition that could result in, from night to night, instability in model fitting in terms of how much flux gets assigned to the different model components. This instability results in additional noise in the Hβ light curve. To minimize the noise due to degeneracy from spectral fits, we used a version of the decomposed model spectra where only the AGN and stellar continuum components have been removed. This version consisted of the residuals of all present emission lines after continuum subtraction. We then selected a corresponding extraction window free of other emission lines for the calculation of Hβ flux (see Table 5). A different way to extract Hβ flux is to use a version of the decomposed model spectra that only contained Hβ broad and narrow components, with other emission-line components as well as the AGN and stellar continua removed. The resulting Hβ light curves computed from the two methods were very similar for objects that have relatively clean Hβ spectral regions, but those for the emission-line residual versions were less noisy for objects with more complex line profiles within the Hβ spectral region. The final Hβ light-curve measurements for the full sample are presented in Table 6. The light curves for the V band and Hβ are shown in Figures 4–10. The rest of the emission-line features will be presented in a forthcoming paper.
Figure 4. Light curves for the LAMP2016 sample (Zw 535−012, I Zw 1, Mrk 1048): V-band continuum flux density fλ in 10−15 erg cm−2 s−1 Å−1, color-coded by telescopes (top left); the Hβ emission line flux fline in 10−15 erg cm−2 s−1 (bottom left). The error bars plotted here for the Hβ light curves incorporate the uncertainty term from the normalized excess scatter of [O iii]. The cross-correlation function is shown in the right panel for each AGN, alongside the cross-correlation centroid distribution in yellow. The dotted vertical line indicates the median value of the cross-correlation function (CCF).
Download figure:
Standard image High-resolution imageFigure 5. Same as Figure 4, but for Ark 120, Mrk 376, and Mrk 9.
Download figure:
Standard image High-resolution imageFigure 6. Same as Figure 4, but for Mrk 704, MCG +04−22−042, and Mrk 110.
Download figure:
Standard image High-resolution imageFigure 7. Same as Figure 4, but for RBS 1303, Mrk 684, and Mrk 841.
Download figure:
Standard image High-resolution imageFigure 8. Same as Figure 4, but for Mrk 1392, SBS 1518+593, and 3C 382.
Download figure:
Standard image High-resolution imageFigure 9. Same as Figure 4, but for NPM1G+27.0587, RXJ 2044.0+2833, and PG 2209+184.
Download figure:
Standard image High-resolution imageFigure 10. Same as Figure 4, but for PG 2214+139, RBS 1917, and Mrk 315.
Download figure:
Standard image High-resolution imageTable 5. Emission-line Extraction Windows in Å (observed frame), Fvar, and [O iii] Excess Scatter
| Object | Hβ | Fvar | [O iii] | σ[O iii] |
|---|---|---|---|---|
| Zw 535–012 | 5018–5181 | 0.050 | 5220–5270 | 0.016 |
| I Zw 1 | 5099–5199 | 0.044 | 5263–5337 | 0.054 |
| Mrk 1048 | 5002–5153 | 0.071 | 5200–5252 | 0.004 |
| Ark 120 | 4931–5102 | 0.195 | 5143–5200 | 0.043 |
| Mrk 376 | 5069–5201 | 0.064 | 5259–5322 | 0.016 |
| Mrk 9 | 5007–5127 | 0.069 | 5179–5241 | 0.016 |
| Mrk 704 | 4945–5059 | 0.046 | 5126–5192 | 0.015 |
| MCG +04−22−042 | 4986–5079 | 0.268 | 5149–5203 | 0.012 |
| Mrk 110 | 4985–5120 | 0.083 | 5161–5208 | 0.015 |
| RBS 1303 | 5001–5136 | 0.081 | 5185–5251 | 0.019 |
| Mrk 684 | 5032–5131 | 0.058 | 5209–5262 | 0.048 |
| Mrk 841 | 4949–5120 | 0.073 | 5167–5218 | 0.006 |
| Mrk 1392 | 4958–5108 | 0.173 | 5165–5212 | 0.007 |
| SBS 1518+593 | 5191–5310 | 0.051 | 5369–5428 | 0.024 |
| 3C 382 | 5030–5226 | 0.142 | 5268–5342 | 0.067 |
| NPM1G+27.0587 | 5092–5246 | 0.051 | 5289–5352 | 0.024 |
| RXJ 2044.0+2833 | 5040–5187 | 0.055 | 5240–5276 | 0.019 |
| PG 2209+184 | 5147–5280 | 0.122 | 5329–5387 | 0.052 |
| PG 2214+139 | 5110–5260 | 0.028 | 5307–5355 | 0.024 |
| RBS 1917 | 5111–5261 | 0.028 | 5231–5444 | 0.016 |
| Mrk 315 | 5002–5111 | 0.109 | 5174–5236 | 0.016 |
Download table as: ASCIITypeset image
Table 6. Hβ Light-curve Data
| Object | HJD | f | δf (stat) | δf (modified) |
|---|---|---|---|---|
| Mrk 110 | 7509.74 | 690.6 | 0.76 | 10.47 |
| Mrk 110 | 7520.75 | 683.9 | 0.94 | 10.38 |
| Mrk 110 | 7526.73 | 686.3 | 0.96 | 10.42 |
| Mrk 110 | 7527.73 | 678.7 | 0.93 | 10.30 |
| Mrk 110 | 7536.71 | 701.7 | 1.10 | 10.67 |
| Mrk 110 | 7540.71 | 695.0 | 1.05 | 10.56 |
| Mrk 110 | 7541.71 | 717.2 | 1.39 | 10.93 |
| Mrk 110 | 7543.72 | 665.7 | 1.34 | 10.15 |
| Mrk 110 | 7546.72 | 685.8 | 1.13 | 10.43 |
| Mrk 110 | 7549.69 | 683.1 | 1.35 | 10.41 |
Note. Dates are listed as HJD−2450000. Units for emission-line flux f are in 10−15 erg s−1 cm−2. The original δf represents the photon-counting errors on the flux measurement, while the modified δf incorporates the spectral scaling uncertainties from [O iii] scatter.
Only a portion of this table is shown here to demonstrate its form and content. A machine-readable version of the full table is available.
Download table as: DataTypeset image
To account for the residual uncertainties from spectral scaling, we computed the excess variance in the [O iii] light curve for each AGN as the additional uncertainty term. We then combined this excess variance term with the statistical error in quadrature such that
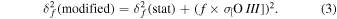
Both the statistical and the modified errors are listed in Table 6. Following Bentz et al. (2009a), we compute the variability statistics Fvar for each light curve and found that it ranges from 0.028 to 0.268, with a median of 0.069 (see Table 5). Almost a third of our sample (3C 382, Ark 120, MCG +04−22−042, Mrk 1392, Mrk 315, and PG 2209+184) exhibit strong variability in the Hβ light curves with Fvar > 0.1. Among the rest of the sample, a few galaxies (such as Zw 535−012, Mrk 110, Mrk 841, RBS 1303, and RXJ2044.0+2833) still display discernible variability for plausible lag determination even if the signal is diluted by large error bars or outliers.
5.1. Integrated Hβ Lags
Following White & Peterson (1994), Peterson et al. (2004), and others, cross-correlation was employed to determine the delay in the integrated Hβ line signal relative to that from the V-band continuum from the photometric campaign. We chose to adopt the interpolated cross-correlation function (e.g., Peterson et al. 1998) method. Given a lag range that represents reasonable bounds of the expected lag, the cross-correlation function (CCF) between the two light curves is computed at every time lag τ at 0.5 day intervals via
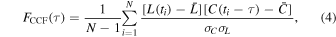
where  (
( ) and σL
(σC
) are the mean and standard deviation of the emission-line (continuum) time series, respectively.
) and σL
(σC
) are the mean and standard deviation of the emission-line (continuum) time series, respectively.
Two lag measures are computed: τpeak, the lag at the peak of the CCF, and τcen, the centroid of the CCF for all points in the CCF above a predetermined threshold value (80% of the peak CCF value). We adopt the latter for the subsequent analysis. For error analysis, we employed the Monte Carlo flux randomization method (Peterson et al. 1998) and repeated the CCF calculation for 103 realizations, building up distributions of correlation measurements. The median and ±1σ widths of the cross-correlation centroid distributions were then adopted as the final lag measurements, and their associated uncertainties as shown in Figures 4–10.
5.2. Assessment of Cross-correlation Reliability
In any RM campaign, it is expected that some AGNs will yield highly robust measurements of reverberation lag, thanks to strong variability and high-quality data, while other objects may exhibit little or no evidence for correlated variability between the continuum and emission-line light curves. This can occur as a result of observational factors including low S/N or poor temporal sampling, or factors intrinsic to the AGNs, including low variability amplitude or low responsivity of the emission line to variations in the ionizing continuum. There is not necessarily a clear demarcation between reliable and unreliable lag measurements, and a variety of methods have been used to assess the significance or quality of lag detections (e.g., Grier et al. 2017). In some cases, a simple threshold value of the correlation strength rmax is used, but rmax alone is not necessarily a good indicator of correlation significance for red-noise light curves. An alternative method is to employ null-hypothesis testing to determine the probability that two uncorrelated red-noise light curves having the same S/N and cadence as the data would yield an rmax at least as strong as the observed value. Such methods have been employed for analysis of multiwavelength continuum correlations in AGNs (e.g., Uttley et al. 2003; Arévalo et al. 2008; Chatterjee et al. 2008), but until recently have rarely been employed to assess broad-line reverberation lags (Penton et al. 2022; Li et al. 2021). Our method will be presented in detail by Guo et al. (in preparation), and we provide a brief description here.
We first generated light curves according to the damped random walk (DRW) model with the Python software CARMA 42 (Kelly et al. 2009, 2014). The DRW model provides an adequate description of ultraviolet/optical variabilities in AGNs, though with plausible deviations on short (McHardy et al. 2006; Mushotzky et al. 2011; Kasliwal et al. 2015; Smith et al. 2018) or long (MacLeod et al. 2010; Guo et al. 2017) timescales. Each simulated light curve represents a segment randomly selected from a 100-times longer light curve predicted from the same DRW model fitted to the observed light curve. We resampled each mock light curve to have the same cadence as the real observations and added Gaussian random noise based on the S/N of the data, creating 103 realizations of each light curve. Cross-correlation measurements were then carried out using the simulated data to determine the distribution of rmax values that would be obtained for uncorrelated light curves. A two-way simulation was performed—that is, we calculated the CCF between the real continuum and each simulated emission-line light curve for the first 500 simulations, and then the opposite way for the rest of the realizations.
We measured the CCF for all of the simulations, using the same lag search range employed for each AGN, and counted, out of 103, the number of positive lags (τ > 0) with peak values  higher than our observed
higher than our observed 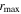 . The resulting fraction represents the probability that a correlation signal found between two uncorrelated light curves would exceed the correlation signal of the data. This derived p-value, denoted
. The resulting fraction represents the probability that a correlation signal found between two uncorrelated light curves would exceed the correlation signal of the data. This derived p-value, denoted 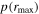 , thus provides an indicator of the robustness of our lag detections given the observed rmax and the observed properties of the light curves including S/N, cadence, and duration.
, thus provides an indicator of the robustness of our lag detections given the observed rmax and the observed properties of the light curves including S/N, cadence, and duration.
We emphasize that the p-values derived from this method are not false-positive probabilities, and they do not give a measure of the absolute “significance” of a lag detection. Strictly speaking, our p-values simply give the probability that uncorrelated light curves having the same statistical properties as the data would give a cross-correlation signal as strong as that seen in the data. Consequently, a smaller p-value denotes a more robust and reliable detection of the correlation signal between two light curves. In general, for broad-line RM, we have a strong prior that a reverberation signal is very likely to be present in the data; thus, our null hypothesis of intrinsically uncorrelated light curves is an extreme and fairly unlikely scenario. We further emphasize that there is no strict cutoff between significant and insignificant lag detections by this method; the p-value merely gives an indication of the relative degree of reliability between different measurements.
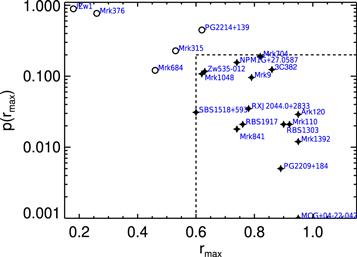
We assess the quality of our resulting lags based on these quantitative assessment indicators in Figure 11. As expected, there is an anticorrelation between rmax and 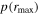 , but it is not a tight one-to-one relationship owing to the differences in S/N, sampling cadence, and variability amplitude among our sample. The results are consistent with the general expectation that the highest-quality light curves that exhibit clear correlated variability have high
, but it is not a tight one-to-one relationship owing to the differences in S/N, sampling cadence, and variability amplitude among our sample. The results are consistent with the general expectation that the highest-quality light curves that exhibit clear correlated variability have high 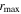 and small
and small 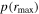 values. Considering these lag-assessment results, we conclude that 16 of the 21 AGNs in our sample falling in the region
values. Considering these lag-assessment results, we conclude that 16 of the 21 AGNs in our sample falling in the region 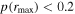 and
and 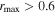 have correlations between continuum and Hβ light curves that are sufficiently robust for the ensuing analyses (noting that they display a broad range of p-values and thus range from highly robust to relatively weak detections of correlated variability), while we discard the remaining five objects from further analysis based on their low rmax and high p-values. Based partly on visual inspection of the light-curve quality, our chosen rmax threshold is relatively conservative compared to those selected by other large surveys (e.g., minimum rmax = 0.45 by SDSS-RM; Grier et al. 2017). These
have correlations between continuum and Hβ light curves that are sufficiently robust for the ensuing analyses (noting that they display a broad range of p-values and thus range from highly robust to relatively weak detections of correlated variability), while we discard the remaining five objects from further analysis based on their low rmax and high p-values. Based partly on visual inspection of the light-curve quality, our chosen rmax threshold is relatively conservative compared to those selected by other large surveys (e.g., minimum rmax = 0.45 by SDSS-RM; Grier et al. 2017). These 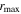 and
and 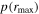 values, along with AGN luminosities and lag measurements τcen in both observed and rest frames, are reported in Table 7. (Only the
values, along with AGN luminosities and lag measurements τcen in both observed and rest frames, are reported in Table 7. (Only the 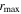 and
and 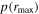 are reported for the subsample of sources with unreliable lag measurements).
are reported for the subsample of sources with unreliable lag measurements).
Figure 11.
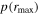 vs.
vs. 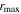 as two objective lag-assessment parameters for our sample. Sources with
as two objective lag-assessment parameters for our sample. Sources with 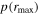 above 0.2 or
above 0.2 or 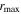 less than 0.6 are deemed to have unreliable lags as represented by open circles.
less than 0.6 are deemed to have unreliable lags as represented by open circles.
Download figure:
Standard image High-resolution imageTable 7. AGN Luminosity and Hβ Cross-correlation Lag Results
| Object | λ Lλ (5100 Å) | Observed Frame | Rest Frame |
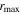
|
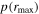
| BLR Kinematics | ||
|---|---|---|---|---|---|---|---|---|
| τcen | τpeak | τcen | τpeak | |||||
| (1043 erg s−1) | (days) | (days) | (days) | (days) | ||||
| Zw 535−012 | 4.9 ± 0.7 |
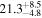
|
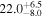
|
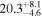
|
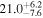
| 0.63 | 0.12 | Infalling |
| Mrk 1048 | 9.5 ± 1.8 |
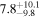
|
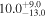
|
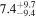
|

| 0.62 | 0.11 | Infalling |
| Ark 120 | 9.2 ± 3.4 |
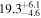
|
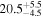
|
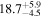
|
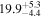
| 0.95 | 0.03 | Ambiguous |
| Mrk 9 | 5.6 ± 0.4 |
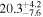
|
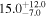
|
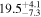
|
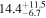
| 0.79 | 0.10 | Ambiguous |
| Mrk 704 | 6.2 ± 0.6 |
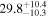
|
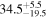
|
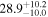
|

| 0.82 | 0.19 | Infalling |
| MCG +04−22−042 | 1.6 ± 0.4 |
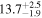
|
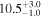
|
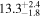
|
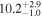
| 0.95 | 0.00 | Symmetric |
| Mrk 110 | 7.2 ± 1.7 |
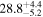
|
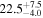
|
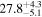
|
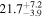
| 0.92 | 0.02 | Symmetric |
| RBS 1303 | 2.4 ± 0.4 |
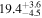
|
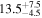
|
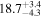
|
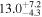
| 0.90 | 0.02 | Outflowing |
| Mrk 841 | 6.7 ± 0.9 |
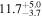
|
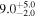
|
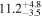
|
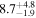
| 0.74 | 0.02 | Infalling |
| Mrk 1392 | 1.6 ± 0.6 |
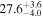
|
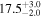
|
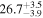
|
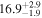
| 0.95 | 0.01 | Symmetric |
| SBS 1518+593 | 10.6 ± 1.0 |
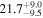
|
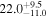
|
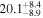
|
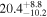
| 0.60 | 0.03 | Infalling |
| 3C 382 | 15.0 ± 3.1 |
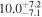
|
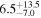
|
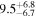
|
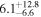
| 0.86 | 0.12 | Symmetric |
| NPM1G +27.0587 | 10.9 ± 1.0 |
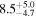
|
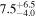
|
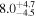
|
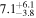
| 0.74 | 0.16 | Infalling |
| RXJ 2044.0+2833 | 5.3 ± 0.5 |
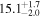
|
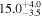
|

|
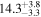
| 0.78 | 0.04 | Infalling |
| PG 2209+184 | 2.3 ± 0.6 |
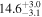
|
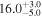
|
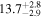
|
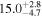
| 0.89 | 0.01 | Ambiguous |
| RBS 1917 | 4.9 ± 0.5 |
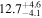
|
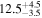
|
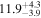
|
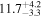
| 0.76 | 0.02 | Outflowing |
| I Zw 1 | 28.5 ± 4.0 | ⋯ | ⋯ | ⋯ | ⋯ | 0.18 | 0.89 | ⋯ |
| Mrk 376 | 17.6 ± 1.8 | ⋯ | ⋯ | ⋯ | ⋯ | 0.26 | 0.77 | ⋯ |
| Mrk 684 | 8.3 ± 0.9 | ⋯ | ⋯ | ⋯ | ⋯ | 0.46 | 0.12 | ⋯ |
| PG 2214+139 | 21.2 ± 1.3 | ⋯ | ⋯ | ⋯ | ⋯ | 0.62 | 0.45 | ⋯ |
| Mrk 315 | 3.2 ± 0.4 | ⋯ | ⋯ | ⋯ | ⋯ | 0.53 | 0.23 | ⋯ |
Download table as: ASCIITypeset image
5.3. Velocity-resolved Hβ Lags
To obtain velocity-resolved reverberation results as a means to probe the kinematics of the BLR gas, we used CCF to compute lag measurements for individual velocity segments of the emission line. Our procedure follows that described by Bentz et al. (2009b), Denney et al. (2009), and Grier et al. (2013), and is detailed below.
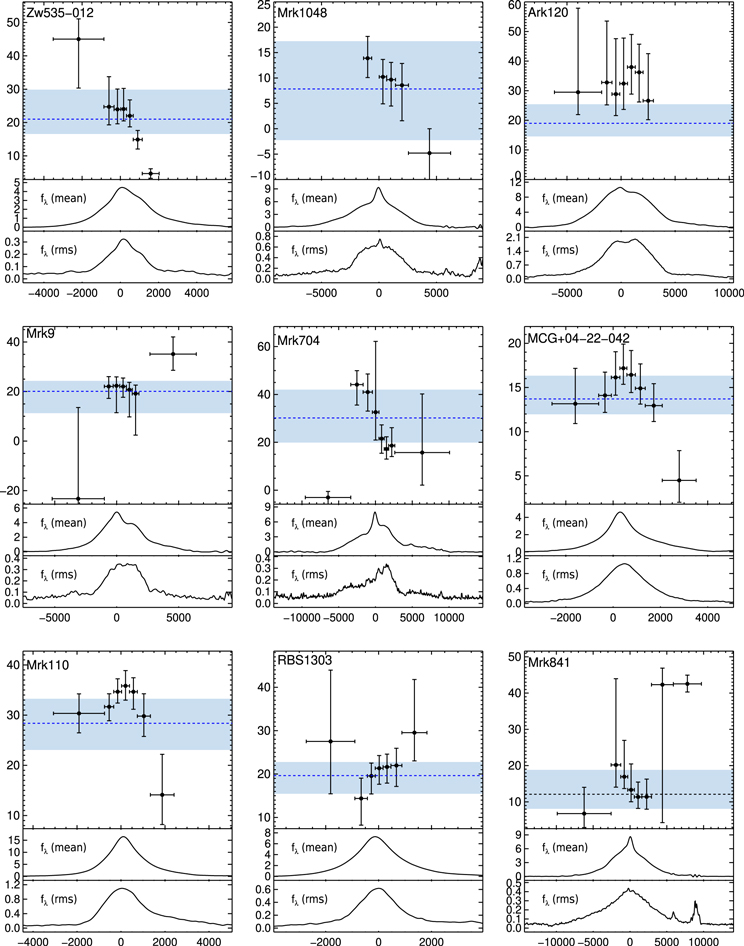
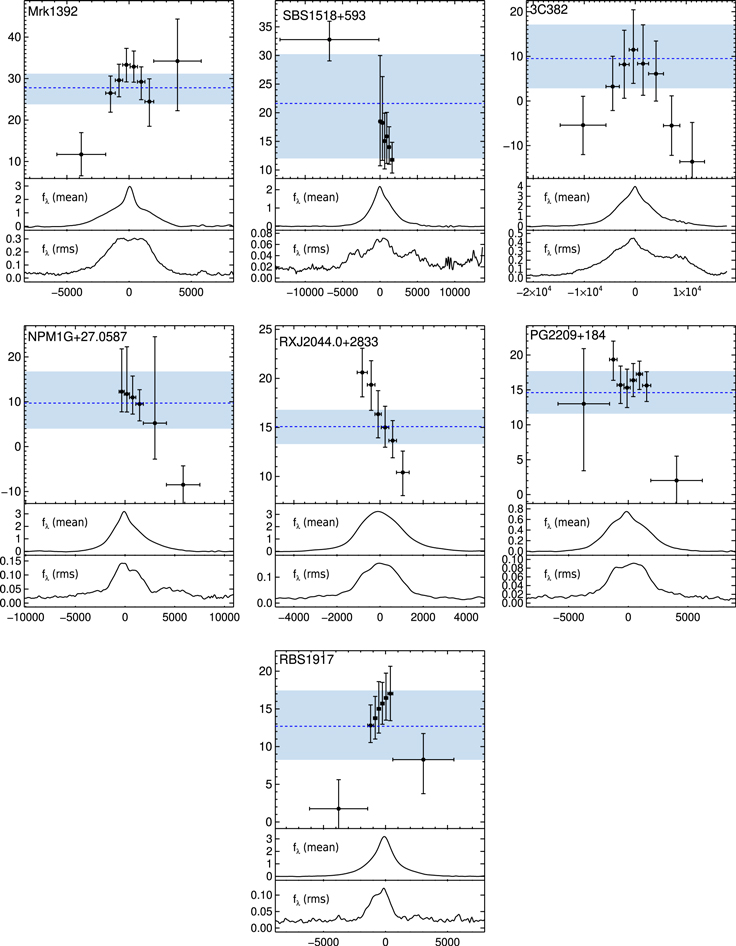
To verify the effect of binning on the apparent BLR kinematics, we divided the broad Hβ component into eight bins via two different schemes: (i) bins of equal-rms flux, and (ii) bins of equal velocity width. In the first approach, we initially determined the total rms flux from integrating the Hβ line in the e-rms spectrum. Then we established velocity bins such that the rms flux within each bin would equal one-eighth of the total flux. There are some exceptions in the cases where the red wing of the rms profile suffered from significant noise, and the last bin was thus truncated at the red line wing. In the second approach, bins are divided evenly across the width of the line in velocity space. In either binning scheme, light curves were computed from each bin of the continuum-subtracted Hβ profile, and lags were measured against the V-band continuum light curve. Resulting lags from the two binning schemes generally agree in the line’s core where the S/N is high; minor disagreement is found in the noisy line wings of some sources. For clarity, we adopt the first scheme (equal-rms-flux binning) and show the resulting velocity-resolved lag spectra for each AGN with robust lag in Figure 12 and in Table 8.
Download figure:
Standard image High-resolution imageFigure 12. Velocity-resolved reverberation lags for our sample. In each of the top panels, the Hβ lags in days (y-axis) shown are for bins of equal-rms flux, plotted against relative velocity in kilometers per second (x-axis). The blue dotted line indicates the overall integrated Hβ lag with ± 1σ uncertainty spanned by the blue bar. The middle and bottom panels show the Hβ profile of the mean and rms spectra, respectively.
Download figure:
Standard image High-resolution imageTable 8. Velocity-resolved Lags
| Object | Velocity Bin | τcen |
|---|---|---|
| (km s−1) | (days) | |
| Mrk110 | −1910 ± 2324 |
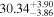
|
| Mrk110 | −539 ± 417 |
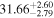
|
| Mrk110 | −151 ± 357 |
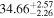
|
| Mrk110 | 205 ± 357 |
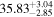
|
| Mrk110 | 563 ± 357 |
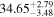
|
| Mrk110 | 1040 ± 596 |
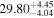
|
| Mrk110 | 1874 ± 1073 |
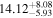
|
Only a portion of this table is shown here to demonstrate its form and content. A machine-readable version of the full table is available.
Download table as: DataTypeset image
5.4. Implications for BLR Kinematics
The velocity-resolved lags allow us to make simple qualitative inferences about the BLR geometry and kinematics from the transfer-function models (e.g., Welsh & Horne 1991; Horne et al. 2004; Bentz et al. 2009b). Qualitatively, symmetric velocity-resolved structure around zero velocity is consistent with either Keplerian, disk-like rotation or random motion without net radial inflow or outflow over an extended BLR. In such a case, the high-velocity wings exhibit the shortest lags because the highest rotation speeds correspond to material orbiting closest to the central black hole. Radially infalling gas produces an asymmetric pattern displaying longer lags at the high-velocity blue wing, while the opposite is true in the case of outflow-dominated kinematics. We note that the presence of absorption, noise, or other geometric complexities may muddle these interpretations, which could be elucidated with direct modeling using forward-modeling codes such as CARAMEL in follow-up work (L. Villafaña et al. 2021, in preparation).
We find a diversity of velocity-resolved lag spectra among our sample representing the qualitative signature of symmetric (3C 382, MCG +04−22−042, Mrk 110, Mrk 1392), infalling (Mrk 1048, Mrk 704, Zw 535−012, Mrk 841, RXJ 2044.0+2833, NPM1G+27.0587, SBS 1518+593), and outflowing (RBS 1303 and RBS 1917) scenarios. In the cases of Ark 120, Mrk 9, and PG 2209+184, the velocity-resolved structure appears flat across the Hβ profile within the uncertainties, which may be difficult to describe with simple models. Whether these kinematics exhibit luminosity-dependent trends and how a subset of these results relates to other RM samples will be further examined in Section 6 and the Appendix, respectively.
6. Black Hole Scaling Relations
6.1. AGN Radius–Luminosity Relationship
The applicability of the radius–luminosity relationship to single-epoch mass determination (Shen et al. 2008; Shen & Liu 2012) relies on the small scatter initially quantified (∼0.2 dex; Kaspi et al. 2005; Bentz et al. 2009a, 2013; Kilerci Eser et al. 2015; Martínez-Aldama et al. 2020), but recent studies of increasingly diverse AGN samples led to an increase in this scatter (e.g., Grier et al. 2017; Du et al. 2018b). The main reason for this increased scatter seems to depend on the Eddington ratio (Bian et al. 2012; Du et al. 2015, 2016; Martínez-Aldama et al. 2019; Dalla Bontà et al. 2020), an important third parameter suggesting that there is more diversity in the AGN population than can be explained by the simple two-parameter radius–luminosity relationship. Here we compare our sample on the AGN radius–luminosity relationship with other RM samples from the literature (Bentz et al. 2013; Grier et al. 2017; Du et al. 2018b) in Figure 13. The best-fit line from SDSS-RM for this relation is
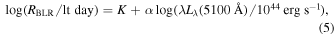
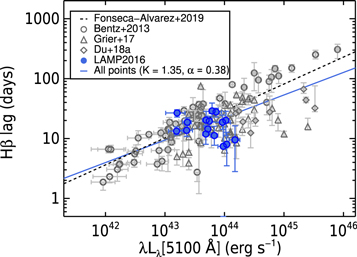
with a median slope α = 0.45 and a median normalization K = 1.46 (Fonseca Alvarez et al. 2020). We computed the AGN luminosity λ Lλ (5100 Å) based on the AGN continuum flux at 5100 Å as extracted from the decomposition of the mean spectrum. Luminosity distances were derived using the cosmology calculator (H0 = 67.8 km s−1 Mpc−1) provided by Wright (2006). All of our AGNs fall within 0.5 dex of the radius–luminosity relation as defined by the literature points within the range of λ Lλ (5100 Å) = 1043.5–44.4 erg s−1. The best-fit line in the form of Equation (5) for all of the data points combining our current work with those from the literature has a normalization K = 1.35 and α = 0.38.
Figure 13. Radius–luminosity relationship of our sample (blue, filled) superimposed on top of other work from the literature (open symbols; Bentz et al. 2013; Grier et al. 2017; Du et al. 2018b). The best-fit relation from SDSS with a median slope α of 0.45 and a median normalization K of 1.46 (Fonseca Alvarez et al. 2020) is plotted as the dashed line. The best-fit line in the form of Equation (5) for all of the data points combining our current work with those from the literature (blue) has a normalization K = 1.35 and α = 0.38.
Download figure:
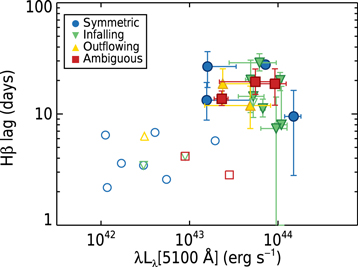
Standard image High-resolution imageWe further explore whether BLR kinematics might depend on AGN luminosity. Past work has shown that while inflow or outflow are indicated in a subset of AGNs, the majority of Hβ velocity-delay maps appear roughly symmetric with rotationally dominated kinematics (e.g., Bentz et al. 2009b, 2010b; Denney et al. 2010; Barth et al. 2011; Horne et al. 2021). The AGNs with velocity-resolved reverberation detected to-date are mostly within the low-luminosity range [λ Lλ (5100 Å) = 1042–43.5 erg s−1]. Our results add significantly to the existing number of sources having velocity-resolved measurements with λ Lλ (5100 Å) ≈ 1044 erg s−1. While we caution that velocity-resolved lag spectra provide only a qualitative impression of the BLR kinematics, we illustrate the BLR kinematics via different colored symbols shown alongside those from the literature in Figure 14. No trend is seen between BLR kinematics and AGN luminosity either within our LAMP2016 sample or when combined with past results from the literature. It is plausible that the BLR shows time-dependent structural changes, from both the kinematic and the geometric points of view, and there may be a lag in its correlation with the luminosity of the AGN. The diversity in BLR kinematics found in our moderately high-luminosity sample appears consistent with that seen among AGNs with super-Eddington accretion rates (e.g., Du et al. 2016b).
Figure 14. Radius–luminosity relationship of our sample (filled and color-coded by BLR kinematics) along with other velocity-resolved results from Bentz et al. (2010a), Pancoast et al. (2014b), Grier et al. (2013), De Rosa et al. (2018), and Du et al. (2018b; open symbols with the same color coding). No trend is seen for the different BLR kinematics within our LAMP2016 sample or when combined with the literature.
Download figure:
Standard image High-resolution image6.2. Hβ Line Widths
Following the procedure outlined by Barth et al. (2015), we measured the line width of the broad Hβ component from both the spectrally decomposed mean spectrum and the rms spectrum. The mean spectrum constructed from the time-series data has a continuum level of zero with just residual noise from spectral fitting, but the continuum of the rms spectrum incorporates photon-counting errors in addition to residual noise. The noise continuum is removed after a simple linear fit before making line width measurements.
We computed the line width using two separate parameters according to Peterson et al. (2004): the FWHM intensity of the line, and the line dispersion σline. The FWHM of a single-peaked line is defined as the difference between the wavelengths blueward and redward of the peak 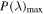 that correspond to half of its height. A double-peaked line requires additional attention to defining
that correspond to half of its height. A double-peaked line requires additional attention to defining  for the blue and red peaks, respectively, and thus their corresponding wavelengths at half the maximum height, but otherwise the procedure in determining the difference between the resulting wavelengths is similar. As for σline (square root of the second moment of the Hβ line profile), we adopted from Peterson et al. (2004) the following:
for the blue and red peaks, respectively, and thus their corresponding wavelengths at half the maximum height, but otherwise the procedure in determining the difference between the resulting wavelengths is similar. As for σline (square root of the second moment of the Hβ line profile), we adopted from Peterson et al. (2004) the following:

where
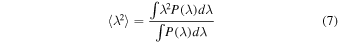
and

In each of these calculations, we also varied the endpoints of the Hβ extraction window randomly within ±5 Å ten times in order to account for uncertainties brought about by the precise choice of the Hβ spectral limits. The resulting line width measurement is the mean from these ten trials.
For error analysis associated with the measured width parameters, we undertook a Monte Carlo bootstrapping procedure and simulated 100 realizations of the mean and rms spectra, respectively, based on random subset sampling of the existing nightly spectra. For a source with n epochs of observations, we simulate new mean and rms spectra of the broad Hβ component from combining n randomly drawn time-series spectra with repetition allowed. We repeated our measurement of the FWHM and σline on these new spectra, where the means and the standard deviations of the resulting distributions were taken as the line widths and their corresponding uncertainties, respectively.
The final line width measurements are corrected for instrumental broadening subtracted in quadrature from the observed line width Δλobs:

Given that we used the same blue-side spectral setup as the LAMP2011 campaign, we adopt from Barth et al. (2015) the instrumental FWHM of 380 km s−1 and dispersion σinst ≈162 km s−1 for our small corrections. The resulting FWHM and σline measured from both the mean and the e-rms spectra are presented in Table 9.
Table 9. Rest-frame Line Widths of the Broad Hβ Component
| Mean | rms | |||
|---|---|---|---|---|
| Object | FWHM | σline | FWHM | σline |
| Zw 535−012 | 2705 ± 33 | 1474 ± 28 | 2005 ± 80 | 1259 ± 112 |
| I Zw 1 | 2187 ± 920 | 1644 ± 102 | 2665 ± 700 | 916 ± 165 |
| Mrk 1048 | 4830 ± 80 | 1840 ± 58 | 4042 ± 406 | 1726 ± 76 |
| Ark 120 | 5656 ± 44 | 2125 ± 41 | 4765 ± 84 | 1882 ± 42 |
| Mrk 376 | 10055 ± 341 | 2662 ± 38 | 14438 ± 1439 | 3633 ± 210 |
| Mrk 9 | 3751 ± 71 | 1555 ± 68 | 3159 ± 144 | 1326 ± 69 |
| Mrk 704 | 8597 ± 448 | 2002 ± 63 | 8597 ± 448 | 2009 ± 102 |
| MCG +04−22−042 | 2658 ± 57 | 1141 ± 39 | 2120 ± 39 | 977 ± 29 |
| Mrk 110 | 2048 ± 13 | 1203 ± 32 | 2052 ± 100 | 1314 ± 69 |
| RBS 1303 | 2286 ± 21 | 1243 ± 26 | 1738 ± 113 | 1292 ± 156 |
| Mrk 684 | 2174 ± 33 | 1216 ± 74 | 2391 ± 632 | 2010 ± 773 |
| Mrk 841 | 7073 ± 311 | 2139 ± 55 | 7452 ± 660 | 2278 ± 96 |
| Mrk 1392 | 4267 ± 25 | 1635 ± 13 | 3690 ± 138 | 1501 ± 38 |
| SBS 1518+593 | 3312 ± 24 | 1782 ± 21 | 4656 ± 1692 | 2249 ± 255 |
| 3C 382 | 7772 ± 54 | 4218 ± 67 | 13926 ± 2337 | 5616 ± 97 |
| NPM1G +27.0587 | 3501 ± 28 | 1683 ± 42 | 2893 ± 177 | 1735 ± 136 |
| RXJ 2044.0+2833 | 2196 ± 31 | 989 ± 32 | 2047 ± 72 | 870 ± 50 |
| PG 2209+184 | 4045 ± 34 | 1573 ± 40 | 3247 ± 88 | 1353 ± 64 |
| PG 2214+139 | 5133 ± 17 | 1947 ± 55 | 4867 ± 473 | 1984 ± 90 |
| RBS 1917 | 2399 ± 11 | 1180 ± 50 | 1653 ± 287 | 851 ± 154 |
| Mrk 315 | 3097 ± 252 | 1824 ± 67 | 3411 ± 1438 | 2031 ± 260 |
Note. All line width measurements are in kilometers per second.
Download table as: ASCIITypeset image
6.3. Virial Black Hole Masses
The mass of a black hole may be determined most robustly using dynamical modeling codes such as CARAMEL (e.g., Pancoast et al. 2011). Nonetheless, virial estimates are useful within uncertainties that depend on the BLR geometry. The black hole mass and its associated uncertainty are computed and propagated from the virial equation


where f is the scaling factor that depends on the geometry and kinematics of the BLR, c is the speed of light, τ ± στ
is the time delay with uncertainties, v ± σv
is the velocity of the BLR gas with uncertainties as measured by the line width, and G is the gravitational constant. The empirically fitted virial factor from Woo et al. (2015) is consistent with that from CARAMEL dynamical modeling (Pancoast et al. 2014b), so we have adopted for our black hole mass calculations 〈f〉 = 100.65 = 4.47 from Woo et al. (2015), τ = τcen, and v = σline(rms) from Dalla Bontà et al. (2020) to facilitate comparisons with other studies. We present both the virial products 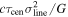 and the derived f-dependent black hole masses in Table 10. Comparisons of our results to existing prior black hole mass measurements for several sources can be found in the Appendix. Overall, we find agreements between our measurements and those from the literature within uncertainties.
and the derived f-dependent black hole masses in Table 10. Comparisons of our results to existing prior black hole mass measurements for several sources can be found in the Appendix. Overall, we find agreements between our measurements and those from the literature within uncertainties.
Table 10. Virial Products and Derived BH Masses
| Object |
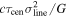
|
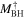
|
|---|---|---|
| (107 M⊙) | (108 M⊙) | |
| Zw 535−012 |
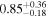
|
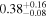
|
| Mrk 1048 |
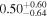
|
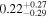
|
| Ark 120 |
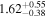
|
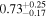
|
| Mrk 9 |

|
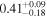
|
| Mrk 704 |
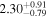
|
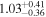
|
| MCG +04−22−042 |
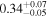
|
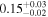
|
| Mrk 110 |
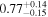
|
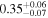
|
| RBS 1303 |
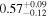
|
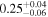
|
| Mrk 841 |
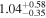
|
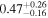
|
| Mrk 1392 |
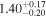
|
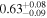
|
| SBS 1518+593 |
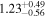
|
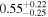
|
| 3C 382 |
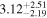
|
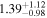
|
| NPM1G +27.0587 |
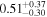
|
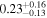
|
| RXJ 2044.0+2833 |
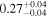
|
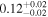
|
| PG 2209+184 |
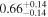
|
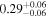
|
| RBS 1917 |

|
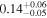
|
Note.†Assuming f = 4.47 (Woo et al. 2015).
Download table as: ASCIITypeset image
7. Conclusions
We present the first results from our 100-night LAMP2016 campaign where we monitored a sample of 21 luminous Seyfert 1 nuclei with AGN luminosity λ Lλ (5100 Å) ≈1044 erg s−1 during 2016 April–2017 May at Lick Observatory. Our analysis here provided the Hβ emission-line light curves and integrated Hβ lag detections measured against V-band continuum photometric light curves for the full sample. We further assessed the significance of the lag determinations, and computed, for a subset of sources with good-quality lags, their velocity-resolved reverberations, inferred BLR kinematics, broad Hβ line widths, and virial black hole mass estimates.
The unusually rainy weather at Mount Hamilton during the winter months of 2016–2017 hampered our ability to monitor the variability of our AGNs as closely as would have been ideal, leaving large gaps in several of our emission-line light curves. Consequently, we were not able to measure reliable lags for six of our AGNs owing to inadequate light curves. Our overall results nearly double the number of existing velocity-resolved lag measurements, particularly at the moderately high-luminosity regime among previous reverberation-mapped samples, and revealed a diversity of signatures potentially indicative of different BLR gas kinematics. Given the complexity of the multiple factors involved, the lack of any clear correlation between AGN luminosity and velocity-resolved lag structure suggests that luminosity itself is not the sole factor responsible for setting the kinematic state of the BLR. It may also depend on other properties of the accreting black holes. Follow-up direct dynamical modeling work will shed light on the detailed kinematics and provide robust dynamical black hole masses to help further calibrate widely adopted black hole scaling relations.
We thank the anonymous referee for thoughtful comments and great suggestions that significantly improved this manuscript. We are grateful to M. Fausnaugh for offering help with their mapspec code used to test different spectral scaling of our Shane/Kast data, and M. Bentz for providing her table of values for the radius–luminosity relationship. We acknowledge the following individuals for their time and effort contributed to the Lick observing campaign: (Shane) Zachary Parsons, Estefania Padilla Gonzalez, Noah Rivera, Cristilyn Gardner, Jake Haslemann, Sean Lewis, and Ellen Glad; (Nickel) Nick Choksi, Sameen Yunus, Jeff Molloy, Andrew Rikhter, and Haynes Stephens. Photometric data collection at MLO was supported by NSF grant AST-1210311; we thank Robert Quimby, Emma Lee, Joseph Tinglof, Eric McLaughlin, Amy Igarashi, and Tariq Johnson for assistance with these observations.
We are deeply grateful to the UCO/Lick staff for help with scheduling and supporting the observations. Research at Lick Observatory is partially supported by a generous gift from Google. The Kast red CCD detector upgrade, led by B. Holden, was made possible by the Heising-Simons Foundation, William and Marina Kast, and the University of California Observatories. KAIT and its ongoing operation were made possible by donations from Sun Microsystems, Inc., the Hewlett-Packard Company, AutoScope Corporation, Lick Observatory, the NSF, the University of California, the Sylvia & Jim Katzman Foundation, and the TABASGO Foundation. Data presented herein were obtained using the UCI Remote Observing Facility, made possible by a generous gift from John and Ruth Ann Evans.
Research at UC Irvine has been supported by NSF grants AST-1412693 and AST-1907208. V.U. acknowledges funding support from the University of California Riverside’s Chancellor’s Postdoctoral Fellowship and NASA Astrophysics Data Analysis Program Grant #80NSSC20K0450. Her work was conducted in part at the Aspen Center for Physics, which is supported by NSF grant PHY-1607611; she thanks the Center for its hospitality during the “Astrophysics of Massive Black Holes Merger” workshop in 2018 June and July. T.T. acknowledges support by the Packard Foundation through a Packard research fellowship. V.N.B. and I.S. gratefully acknowledge assistance from NSF Research at Undergraduate Institutions (RUI) grants AST-1312296 and AST-1909297. Note that findings and conclusions do not necessarily represent views of the NSF. G.C. acknowledges NSF support under grant AST-1817233. J.H.W. acknowledges the funding from the Basic Science Research Program through the National Research Foundation of Korean Government (NRF-2021R1A2C3008486). A.V.F.'s group at U.C. Berkeley is grateful for support from the TABASGO Foundation, the Christopher R. Redlich Fund, the Miller Institute for Basic Research in Science (in which he is a Miller Senior Fellow), and many individual donors. K.H. acknowledges support from STFC grant ST/R000824/1. We acknowledge the generous support of Marc J. Staley, whose fellowship partly funded B.E.S. while contributing to the work presented herein as a graduate student. I.S. acknowledges support from the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germanys Excellence Strategy—EXC 2121 “Quantum Universe”—390833306. Research by S.V. is supported by NSF grants AST1813176 and AST-2008108.
This work makes use of observations from the LCOGT network. The Liverpool Telescope is operated on the island of La Palma by Liverpool John Moores University in the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofisica de Canarias with financial support from the UK Science and Technology Facilities Council. Based on observations acquired at the Observatorio Astronómico Nacional in the Sierra San Pedro Mártir (OAN-SPM), Baja California, México, we thank the daytime and night support staff at the OAN-SPM for facilitating and helping obtain our observations. Some of the data used in this paper were acquired with the RATIR instrument, funded by the University of California and NASA Goddard Space Flight Center, and the 1.5-meter Harold L. Johnson telescope at the Observatorio Astronómico Nacional on the Sierra de San Pedro Mártir, operated and maintained by the Observatorio Astronómico Nacional and the Instituto de Astronomía of the Universidad Nacional Autónoma de México. Operations are partially funded by the Universidad Nacional Autónoma de México (DGAPA/PAPIIT IG100414, IT102715, AG100317, IN109418, IG100820, and IN105921). We acknowledge the contribution of Leonid Georgiev and Neil Gehrels to the development of RATIR. This research was made possible through the use of the AAVSO Photometric All-Sky Survey (APASS), funded by the Robert Martin Ayers Sciences Fund and NSF grant AST-1412587 and contributed by observers worldwide. We acknowledge the use of The AGN Black Hole Mass Database as a compilation of some of the reverberation-mapped black hole masses prior to 2015 (Bentz & Katz 2015). This research has made use of the NASA/IPAC Extragalactic Database (NED), which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration.
Facilities: Shane (Kast double spectrograph) - , KAIT - , Nickel - , LCOGT - , MLO:1m - , OANSPM:1.5m - , FLWO:1.2m - , BYU:0.9m - , Liverpool:2m - , AAVSO - .
Software: mpfit (Markwardt 2009), CARMA (Kelly et al. 2009, 2014), IDL Astronomy User’s Library (Landsman 1993), IRAF (Tody 1986), CARAMEL (Pancoast et al. 2011, 2014a, Villafana et al.,in prep.), mapspec (Fausnaugh 2017).
Appendix: Comparison with Prior MBH Measurements
RM studies over the years have shown the intrinsic scatter among BH mass measurements from the RM technique to be inherently small, demonstrating its robustness for measuring BH masses. In the well-studied case of NGC 5548 with many epochs of RM-based BH masses (see Dalla Bontà et al. 2020, for a recent compilation), the distribution of these masses exhibits an intrinsic scatter of about 0.2 dex, suggesting that reverberation BH mass measurements for individual sources may typically fall within this range. Here we examine the level of agreement between our results and those from the literature for the AGNs where BH mass measurements from previous RM campaigns are available. Given the expected ∼0.2 dex scatter in mass estimates obtained from light curves at different epochs, our measurements for the majority of these sources are generally consistent with past MBH estimates, with a factor of 2.7 difference (0.44 dex) in the most discrepant case. Unfortunately, we were unable to measure a BH mass for I Zw 1 given the small variations in the Hβ light curve observed during our monitoring period, but we note that a mass of 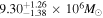 has previously been determined by (Huang et al. 2019).
has previously been determined by (Huang et al. 2019).
A.1. Ark 120
Ark 120 was monitored by Peterson et al. (1998) and Peterson et al. (2004) who had measured a rest-frame Hβ lag of 47.1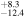 and
and 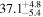 days and σline of 1959 ± 109 and 1884 ± 48 km s−1 from two different epochs, respectively. Adopting the same 〈f〉 of 4.47 from Woo et al. (2015) as in this study, the black hole masses calculated are
days and σline of 1959 ± 109 and 1884 ± 48 km s−1 from two different epochs, respectively. Adopting the same 〈f〉 of 4.47 from Woo et al. (2015) as in this study, the black hole masses calculated are 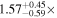 108
M⊙ and
108
M⊙ and 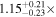 108
M⊙, respectively.
108
M⊙, respectively.
In comparison, we measured a shorter lag of 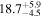 days in Hβ, resulting in a smaller black hole mass of 0.73
days in Hβ, resulting in a smaller black hole mass of 0.73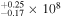 M⊙. In a concurrent campaign, the Monitoring AGNs with Hβ Asymmetry (MAHA) group determined an Hβ lag of
M⊙. In a concurrent campaign, the Monitoring AGNs with Hβ Asymmetry (MAHA) group determined an Hβ lag of 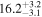 days and consequently a black hole mass of
days and consequently a black hole mass of 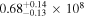 (using the same virial factor) in Ark 120 (Du et al. 2018a). Our measurement (
(using the same virial factor) in Ark 120 (Du et al. 2018a). Our measurement (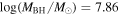 ) is very similar to the MAHA result (
) is very similar to the MAHA result (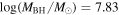 ), and roughly agrees with the previous masses (
), and roughly agrees with the previous masses (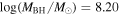 ) from over a decade ago within ±0.2 dex, indicating that the state of the AGN and the intrinsic BLR properties have stayed generally consistent in the past two decades.
) from over a decade ago within ±0.2 dex, indicating that the state of the AGN and the intrinsic BLR properties have stayed generally consistent in the past two decades.
A.2. Mrk 704
Mrk 704 was among five bright Seyfert 1 galaxies that were targeted by De Rosa et al. (2018) in an RM campaign in early 2012. De Rosa et al. 2018 measured an Hβ lag of 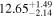 days and σline of
days and σline of 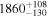 km s−1, resulting in a black hole mass of
km s−1, resulting in a black hole mass of 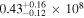 M⊙, or
M⊙, or 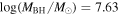 . Four years later, we determined a longer lag of
. Four years later, we determined a longer lag of 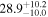 days and a larger σline of 2009 ± 102 km s−1. Our black hole mass measurement of 1.03
days and a larger σline of 2009 ± 102 km s−1. Our black hole mass measurement of 1.03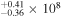 M⊙, or
M⊙, or 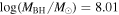 , is more than twice as large as the result from De Rosa et al. (2018), but our measurement’s uncertainty is substantial such that there is statistical agreement within 1.2σ.
, is more than twice as large as the result from De Rosa et al. (2018), but our measurement’s uncertainty is substantial such that there is statistical agreement within 1.2σ.
A.3. Mrk 110
Like Ark 120, Mrk 110 was another RM target monitored by Peterson et al. (1998) and Peterson et al. (2004) within the time period and had a rest-frame Hβ lag of 20.4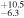 ,
, 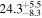 , and
, and  days with σline of 1115 ± 103, 1196 ± 141, and 755 ± 29 km s−1 from three different epochs, respectively. Adopting the same 〈f〉 of 4.47 from Woo et al. (2015) as in this study, the black hole mass calculated correspond to 2.2
days with σline of 1115 ± 103, 1196 ± 141, and 755 ± 29 km s−1 from three different epochs, respectively. Adopting the same 〈f〉 of 4.47 from Woo et al. (2015) as in this study, the black hole mass calculated correspond to 2.2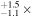 107
M⊙, 3.0
107
M⊙, 3.0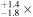 107
M⊙, and 1.7
107
M⊙, and 1.7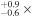 107
M⊙, or a combined value of 2.3
107
M⊙, or a combined value of 2.3 107
M⊙ (
107
M⊙ (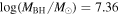 ).
).
With a measured Hβ lag of 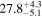 days and a σline of 1314 ± 69 km s−1, we obtained a larger black hole mass of 3.5
days and a σline of 1314 ± 69 km s−1, we obtained a larger black hole mass of 3.5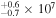 M⊙ (
M⊙ ( ), consistent with the previous estimate within statistical uncertainties (1σ) and ± 0.2 dex.
), consistent with the previous estimate within statistical uncertainties (1σ) and ± 0.2 dex.
A.4. SBS 1518+593
SBS 1518+593 was one target from the MAHA campaign carried out by Du et al. (2018a) during a similar time frame as our LAMP study. Du et al. (2018a) established an Hβ lag of 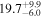 days and σline of 1038 ± 20 km s−1. The inferred black hole mass adjusting for 〈f〉 is
days and σline of 1038 ± 20 km s−1. The inferred black hole mass adjusting for 〈f〉 is 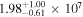 M⊙, or
M⊙, or 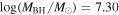 . Measuring a similar lag of
. Measuring a similar lag of 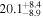 days and larger σline of 2249 ± 255 km s−1, our black hole mass for this AGN was 5.5
days and larger σline of 2249 ± 255 km s−1, our black hole mass for this AGN was 5.5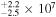 M⊙, or
M⊙, or 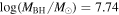 . Our measurements agree statistically within 1.3σ given the large uncertainties, with a difference roughly within ±0.2 dex. However, our velocity-resolved lag spectra disagree qualitatively. Du et al. (2018a) found the BLR kinematics to be in virialized motion while we see infalling behavior. This discrepancy may be due to differences in our respective campaigns’ monitoring durations, where they observed SBS 1518+593 for approximately 180 days while our coverage spanned 360 days. This discrepancy may also be due to the fact that our Hβ light curve exhibits much noise and scatter, which may in turn affect our velocity-resolved measurement.
. Our measurements agree statistically within 1.3σ given the large uncertainties, with a difference roughly within ±0.2 dex. However, our velocity-resolved lag spectra disagree qualitatively. Du et al. (2018a) found the BLR kinematics to be in virialized motion while we see infalling behavior. This discrepancy may be due to differences in our respective campaigns’ monitoring durations, where they observed SBS 1518+593 for approximately 180 days while our coverage spanned 360 days. This discrepancy may also be due to the fact that our Hβ light curve exhibits much noise and scatter, which may in turn affect our velocity-resolved measurement.
A.5. Zw 535-012
The black hole mass in Zw 535-012 was previously determined to be 2.6 × 107
M⊙ (Wang et al. 2009), or 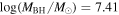 . It was computed using the scaling law from Greene & Ho (2005), assuming
. It was computed using the scaling law from Greene & Ho (2005), assuming  (Hβ) = 42.1 erg s−1 and FWHM(Hβ) = 2555 km s−1 from a single-epoch spectroscopic observation in 2006. In our campaign, we obtained a black hole mass of 3.8
(Hβ) = 42.1 erg s−1 and FWHM(Hβ) = 2555 km s−1 from a single-epoch spectroscopic observation in 2006. In our campaign, we obtained a black hole mass of 3.8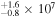 M⊙, or
M⊙, or 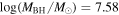 , which is 1.4 times larger than the previous estimate but consistent within statistical uncertainties (0.6σ) and ±0.2 dex.
, which is 1.4 times larger than the previous estimate but consistent within statistical uncertainties (0.6σ) and ±0.2 dex.