Abstract
Homogeneous metallicities and continuous high-precision light curves play key roles in studying the pulsation properties of RR Lyrae stars. By cross matching LAMOST DR6 with the Kepler and K2 fields, we have determined seven and 50 non-Blazhko RRab stars, respectively, that have homogeneous metallicities determined from low-resolution spectra of the LAMOST–Kepler/K2 survey. The Fourier decomposition method is applied to the light curves of these stars provided by the Kepler space-based telescope to determine the fundamental pulsation periods and parameters. The calculated amplitude ratios of R21, R31 and the phase differences of ϕ21, ϕ31 are consistent with the parameters of RRab stars in both globular clusters and the Large Magellanic Cloud. We find a linear relationship between the phase differences ϕ21 and ϕ31, which is in good agreement with the results in the literature. As far as the amplitude, we find that the amplitude of primary frequency A1 and the total amplitude Atot follow either a cubic or linear relationship. For the rise time, we do not find its relevance with the period of the fundamental pulsation mode P1, or Atot and ϕ21. However, it might follow a linear relationship with R31. Based on the homogeneous metallicities, we have derived a new calibration formula for the period–ϕ31–[Fe/H] relation, which agrees well with previous studies.
Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
RR Lyrae stars (hereafter RRLs) are low-mass pulsating stars located at the intersection between the classical instability strip and the horizontal branch of the Hertzsprung–Russell diagram, with helium burning in the core (Aerts et al. 2010). Their pulsations are induced by the so-called κ-mechanism, operating in the hydrogen and helium partial ionization zones. Typical RRLs have pulsation periods of 0.2–1 day, amplitudes of 03 − 1m, effective temperature Teff of 6100–7400 K, and spectral types A2–F6 (Catelan & Smith 2015). According to the pulsation modes, they can be divided into three types, i.e., the fundamental radial mode (type RRab), the first overtone (type RRc), or both modes simultaneously (type RRd) (Guggenberger et al. 2012; Moskalik et al. 2015).
RRLs are widely used as tracers of stellar populations with ages older than 10 Gyr in the Milky Way (Walker 1989; Mullen et al. 2021) and neighboring galaxies (Catelan & Smith 2015; Plachy & Szabo 2021). They are also commonly used as standard candles, benefiting from their relationship between MV and iron abundance (Sandage 1993; Caputo 1998; Nemec et al. 2013). However, this relationship’s intrinsic and systematic errors are still under debate (see, e.g., Caputo et al. 2000; Di Criscienzo et al. 2004; Cassisi et al. 2008; Marconi 2012, 2009; Mullen et al. 2021). The metallicities of RRLs in those studies have been highlighted for a reliable estimation of distance with the period–luminosity–metallicity relation. But it is difficult to obtain accurate measurements of metal abundances of this type of star (For 2011; Govea et al. 2014; Nemec et al. 2013; Sneden et al. 2017; Chadid et al. 2017; Magurno et al. 2019; Crestani et al. 2021; Gilligan et al. 2021). Arellano Ferro (2022) reported a homogeneous approach toward the calculation of mean MV and [Fe/H] with a sample of 37 globular clusters (GCs) via Fourier decomposition of their light curves. Another interesting astrophysical problem of RRLs is the Blazhko effect, which is the amplitude and phase modulation of the light curves on the timescale of tens to thousands of days (Blažko 1907; Shapley 1916). Almost 30%–50% RRLs exhibit Blazhko characteristics, but the physical origin of the effect has remained a mystery since its discovery (Benko et al. 2014).
The investigation of RRLs has made great progress with the unprecedented and ever-precious photometric data obtained by the Kepler and K2 mission. Benko et al. (2010) investigated a sample of 29 RRLs using Kepler photometry and found that almost half of the sample exhibited the Blazhko effect. The prototype star RRL itself was studied in detail with the Q1-Q2 long cadence data of Kepler by Kolenberg et al. (2011), who found a multiplet structure at the main frequency and its harmonics up to the quintuplets. Nemec et al. (2011) carried out a Fourier analysis of 19 non-Blazhko RRab stars with Kepler photometry, among which none showed the period-doubling effect seen in Blazhko stars. They also found that KIC 7021124 pulsates simultaneously in both the fundamental and second overtone modes. Based on the following high-resolution spectroscopic observations with CFHT and Keck I, Nemec et al. (2013) determined the iron-to-hydrogen ratios, radial velocities, and atmospheric parameters for 41 RRLs in the Kepler field and thus gave a new period–ϕ31–[Fe/H] relation. Ngeow (2022) adopted a set of homogeneous samples of fundamental mode RRLs in the Kepler field to investigate the performance of photometric metallicity. After comparisons of roughly 50 RRLs in the prime Kepler field, more than 3000 RRLs have been proposed for observations in K2 campaigns. Although one might lose the chance of studying the Blazhko effect of RRLs by only using K2 photometry concerning the limited lengths of the time-series observations of the target stars, it is still possible to carry out population studies (Molnar et al. 2015; Armstrong et al. 2016) and statistical investigations (Kovacs 2018; Moskalik et al. 2021).
Jurcsik & Kovacs (1996) revealed that the shapes of the light curves of RRab stars in the optical wavelength are relevant due to their metal abundances. They derived a linear relation of metal abundance with period and low-order parameters of Fourier decomposition of the light curves of RRab stars in the V band, with the phase difference of ϕ31 = ϕ3−3ϕ1. This relation was investigated by Smolec (2005) with the light curves in the I band of RRab stars from the Optical Gravitational Lensing Experiment (Udalski et al. 1992). A calibration of the relation was carried out by Ngeow et al. (2016) using the data of the Palomar Transient Factory (Law et al. 2009) in the R band. Nemec et al. (2013) extended the analysis of this relation using well-sampled light curves of RRab stars in the Kepler field (Koch et al. 2010). The calibration of the relation was given by Martinez-Vazquez et al. (2016) using the RRab stars in GCs and fields. Iorio & Belokurov (2021) obtained a new period–ϕ31–[Fe/H] relation using G-band light curves provided by Gaia DR2 (Gaia Collaboration et al. 2018; Holl et al. 2018; Clementini et al. 2019). The recent study of Mullen et al. (2021) not only provided new relations adopting the light curves of RRab stars of an ASAS-SN sample in the V band, but also provided new calibrations for the stars observed in the W1 and W2 WISE bands. A similar study for RRc stars was also carried out by Mullen et al. (2022). Jurcsik & Juhász (2022) studied RRab stars with quasi-identical-shaped light curves but period differences as large as 0.05–0.21 day based on the Galactic bulge data of the OGLE-IV survey. They revealed that several of these stars show very similar light curves to that of the typical bulge RR Lyrae by examining their Fourier parameters. However, to precisely characterize the period–ϕ31–[Fe/H] relation and the connection of the pulsation parameters of RRab stars, homogeneous spectra and light curves are required to derive the metallicity abundances and pulsation parameters, respectively. Fortunately, observations of the LAMOST–Kepler/K2 survey (see, e.g., Cat et al. 2015; Zong et al. 2018; Fu et al. 2020; Wang et al. 2020) have provided LAMOST spectra for a larger number of Kepler/K2 targets. In this study, we investigate the characteristics of the pulsation parameters of non-Blazhko RRab stars based on the Kepler light curves and homogeneous metal abundances provided by the LAMOST–Kepler/K2 survey, and a new calibration of the period–ϕ31–[Fe/H] relation is presented.
This paper is organized as follows: the target selection process is described in Section 2. The Fourier decomposition analysis of light curves is presented in Section 3. An analysis of the results and a discussion are given in Sections 4 and 5, respectively. Finally, we present our conclusions in Section 6.
2. Target Selection
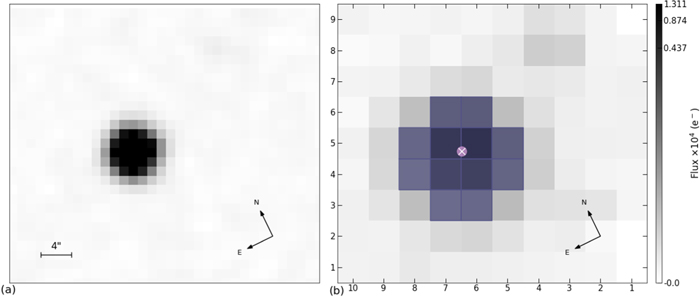
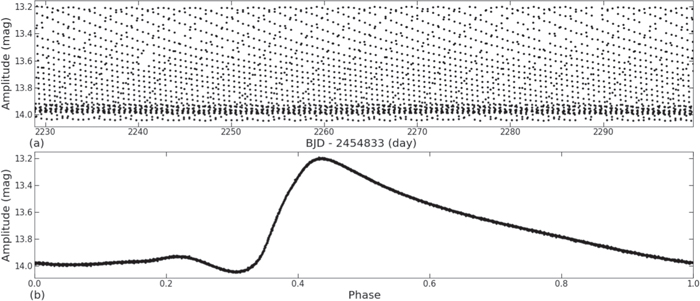
The catalog of RRLs in the fields of K2 was obtained by combining the catalogs of RRLs of all campaigns downloaded from EVEREST (Luger et al. 2016, 2018). We obtained the target pixel files (hereafter TPFs) of all candidates of 3413 stars at the Mikulski Archive for Space Telescopes 4 (MAST; all the K2 data used in this paper can be found at MAST: 10.17909/T9K30X) using the catalogs. The light curves are then extracted from the TPFs with the LightKurve package (Vinícius et al. 2018; Barentsen et al. 2021). For each star, a series of apertures are tested on the TPFs in order to optimize the photometry precision. The extracted light curves are then detrended by fitting and subtracting either a second- or third-order polynomial to remove the long-term systematic errors. Finally, The corresponding fluxes are converted to magnitudes and shifted to the Kp mean magnitude levels. As an example, the images and light curves of the non-Blazhko RRab star EPIC 210830646 observed by K2 are shown in Figures 1 and 2, respectively.
Figure 1. Image of the non-Blazhko RRab star EPIC 210830646. (a) The TPF of the star; (b) the green polygon indicates the optimized aperture adopted on the star for photometry.
Download figure:
Standard image High-resolution imageFigure 2. (a) The light curve of EPIC 210830646 extracted by LightKurve (Vinícius et al. 2018; Barentsen et al. 2021), (b) the phase-folded light curve in the fundamental period.
Download figure:
Standard image High-resolution imageWe identify the non-Blazhko and Blazhko RRLs among those candidates by following the most strict and convincing evidence of whether the presence of the side peaks is shown in the frequency spectra (Skarka et al. 2016). We searched for this feature with the software Period04 (Lenz & Breger 2005), and identified 376 Blazhko and 594 non-Blazhko RRab stars, respectively. Then, we took those non-Blazhko RRab stars to cross match them with the catalog of Liu et al. (2020), who derived the metal abundances of RRLs from the low-resolution spectra of LAMOST DR6, with a total of 50 non-Blazhko RRab stars matched. We also cross-matched the catalog of Liu et al. (2020) with a list of the Kepler non-Blazhko RRab stars in a previous study (Nemec et al. 2013), among which seven stars are derived. As Liu et al. (2020) did not give the uncertainties of the metal abundances of the stars, we estimate the uncertainties using the method provided by Wang et al. (2020). The values of the metal abundances of the 57 non-Blazhko RRab stars, with their corresponding uncertainties of the metal abundances, are listed in the sixth column of Table 1.
Table 1. Properties of Non-Blazhko RRab Stars in the Field of the LAMOST–Kepler/K2 Survey
| No. | ID | Kp | Frequency | Period | [Fe/H] | A1 | RT | Atot | R21 | R31 | ϕ21 | ϕ31 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| KIC/EPIC | (mag) | (c/d) | (day) | (dex) | (mag) | (rad) | (mag) | (rad) | (rad) | |||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) | (12) | (13) |
| 1 | 6100702 | 13.458 | 2.048567(8) | 0.488146(2) | −0.60(6) | 0.2089(5) | 0.200(4) | 0.575(9) | 0.493(2) | 0.279(2) | 2.743(1) | 5.747(1) |
| 2 | 6763132 | 13.075 | 1.701291(3) | 0.587789(1) | −1.90(7) | 0.2802(11) | 0.144(3) | 0.811(19) | 0.471(4) | 0.356(11) | 2.389(2) | 5.096(4) |
| 3 | 7021124 | 13.550 | 1.606443(2) | 0.622493(7) | −1.65(7) | 0.0323(2) | 0.139(1) | 0.831(5) | 0.512(5) | 0.351(5) | 2.372(2) | 5.060(2) |
| 4 | 7030715 | 13.452 | 1.462813(4) | 0.683614(2) | −1.45(7) | 0.2075(6) | 0.177(3) | 0.647(15) | 0.494(3) | 0.303(2) | 2.683(1) | 5.606(1) |
| 5 | 9658012 | 16.001 | 1.875482(5) | 0.533196(3) | −0.70(6) | 0.3108(14) | 0.141(3) | 0.928(30) | 0.498(5) | 0.360(4) | 2.399(2) | 5.156(3) |
| 6 | 9717032 | 17.194 | 1.795615(9) | 0.556912(5) | −1.40(6) | 0.2119(11) | 0.149(5) | 0.633(21) | 0.512(5) | 0.353(5) | 2.403(2) | 5.139(2) |
| 7 | 9947026 | 13.300 | 1.822858(3) | 0.548589(1) | −2.60(7) | 0.2170(5) | 0.193(12) | 0.599(27) | 0.488(2) | 0.282(2) | 2.745(1) | 5.737(2) |
| 8 | 201395405 | 17.558 | 1.622410(1) | 0.616367(7) | −1.55(6) | 0.1661(12) | 0.160(3) | 0.412(10) | 0.386(6) | 0.320(6) | 2.380(17) | 4.92(31) |
| 9 | 201416966 | 14.441 | 1.767199(7) | 0.565867(4) | −2.10(6) | 0.2719(13) | 0.156(3) | 0.804(15) | 0.506(6) | 0.346(5) | 2.466(14) | 5.27(30) |
| 10 | 201454019 | 14.560 | 1.41163(1) | 0.708401(7) | −1.30(6) | 0.1637(7) | 0.188(3) | 0.416(9) | 0.497(4) | 0.305(3) | 2.587(9) | 5.91(24) |
| 11 | 201458397 | 16.842 | 1.604129(1) | 0.623391(6) | −1.50(7) | 0.1884(5) | 0.221(5) | 0.494(8) | 0.442(3) | 0.253(3) | 2.717(9) | 5.71(23) |
| 12 | 201550621 | 12.626 | 1.841698(6) | 0.542977(3) | −1.50(6) | 0.2995(16) | 0.159(7) | 0.893(14) | 0.523(6) | 0.345(6) | 2.472(15) | 5.28(31) |
| 13 | 201611200 | 14.459 | 1.699969(10) | 0.588246(6) | −0.95(6) | 0.1703(8) | 0.173(3) | 0.465(11) | 0.500(4) | 0.329(4) | 2.590(10) | 5.50(26) |
| 14 | 202064491 | 15.000 | 1.746749(2) | 0.572492(1) | −1.20(6) | 0.1959(15) | 0.161(4) | 0.534(14) | 0.500(7) | 0.344(7) | 2.496(17) | 5.34(33) |
| 15 | 210345648 | 15.087 | 1.686611(9) | 0.592905(6) | −1.20(3) | 0.1960(12) | 0.149(5) | 0.583(19) | 0.422(6) | 0.347(5) | 2.401(16) | 5.01(31) |
| 16 | 210454384 | 17.525 | 1.690231(9) | 0.591635(5) | −1.70(6) | 0.2128(11) | 0.186(7) | 0.609(16) | 0.500(6) | 0.314(5) | 2.639(15) | 5.56(31) |
| 17 | 210766289 | 16.398 | 1.774371(9) | 0.563580(5) | −1.25(6) | 0.2085(13) | 0.148(3) | 0.619(13) | 0.489(7) | 0.357(7) | 2.036(19) | 5.57(35) |
| 18 | 210815465 | 16.002 | 1.918090(5) | 0.521352(2) | −1.60(6) | 0.3826(22) | 0.137(5) | 1.140(12) | 0.467(6) | 0.372(6) | 2.344(17) | 4.91(32) |
| 19 | 210830646 | 13.751 | 1.758810(8) | 0.568566(5) | −1.70(5) | 0.2328(16) | 0.129(1) | 0.628(19) | 0.415(6) | 0.336(6) | 2.356(17) | 4.80(32) |
| 20 | 210862813 | 16.312 | 1.441879(7) | 0.693539(5) | −0.85(6) | 0.2223(3) | 0.214(6) | 0.634(5) | 0.481(5) | 0.263(4) | 2.697(12) | 5.62(28) |
| 21 | 210872065 | 16.016 | 1.593511(7) | 0.627545(4) | −1.10(6) | 0.2369(5) | 0.191(5) | 0.637(5) | 0.457(4) | 0.289(3) | 2.653(10) | 5.63(24) |
| 22 | 210934522 | 15.477 | 2.297878(5) | 0.435184(2) | −1.40(6) | 0.3226(16) | 0.147(6) | 0.972(25) | 0.533(6) | 0.368(6) | 2.346(14) | 5.04(31) |
| 23 | 211410664 | 14.280 | 1.830881(8) | 0.546185(4) | −1.15(5) | 0.2275(14) | 0.149(3) | 0.654(21) | 0.507(6) | 0.354(5) | 2.417(14) | 5.19(30) |
| 24 | 211449132 | 15.008 | 1.772059(7) | 0.564315(4) | −1.70(6) | 0.2384(12) | 0.148(2) | 0.666(11) | 0.476(5) | 0.359(5) | 2.389(14) | 5.12(29) |
| 25 | 211484212 | 16.047 | 1.784809(7) | 0.560284(4) | −1.45(7) | 0.2388(13) | 0.152(4) | 0.693(12) | 0.513(5) | 0.347(5) | 2.465(13) | 5.27(29) |
| 26 | 211517414 | 15.601 | 1.537449(7) | 0.650428(4) | −1.70(6) | 0.2475(8) | 0.183(6) | 0.704(14) | 0.510(4) | 0.314(3) | 2.717(9) | 5.65(24) |
| 27 | 211580649 | 14.776 | 1.960661(7) | 0.510032(4) | −1.35(6) | 0.2491(18) | 0.130(4) | 0.705(25) | 0.460(6) | 0.358(6) | 2.320(16) | 4.88(32) |
| 28 | 211620065 | 16.395 | 2.034389(7) | 0.491548(3) | −1.15(7) | 0.2463(17) | 0.136(3) | 0.715(21) | 0.474(6) | 0.363(6) | 2.313(16) | 4.89(31) |
| 29 | 211653001 | 13.329 | 1.906039(7) | 0.524648(3) | −2.00(6) | 0.2478(17) | 0.132(3) | 0.715(23) | 0.449(6) | 0.353(6) | 2.319(16) | 4.84(31) |
| 30 | 211663101 | 14.365 | 1.665351(5) | 0.600474(3) | −0.50(6) | 0.3256(16) | 0.150(6) | 0.952(19) | 0.493(5) | 0.346(5) | 2.418(14) | 5.16(30) |
| 31 | 211918301 | 16.075 | 1.643631(6) | 0.608409(3) | −1.35(6) | 0.2831(6) | 0.188(8) | 0.722(17) | 0.454(3) | 0.293(3) | 2.576(9) | 5.50(24) |
| 32 | 211933496 | 15.414 | 2.058359(7) | 0.485824(3) | −1.75(6) | 0.2516(19) | 0.132(1) | 0.743(19) | 0.457(6) | 0.353(6) | 2.314(16) | 4.85(31) |
| 33 | 212130982 | 13.501 | 1.673371(7) | 0.597596(4) | −1.20(6) | 0.2614(7) | 0.178(2) | 0.772(16) | 0.493(4) | 0.311(4) | 2.600(10) | 5.51(25) |
| 34 | 212182292 | 12.392 | 1.832240(6) | 0.545780(3) | −0.45(6) | 0.2679(9) | 0.172(5) | 0.792(13) | 0.513(4) | 0.326(3) | 2.757(9) | 5.72(24) |
| 35 | 212789652 | 13.764 | 1.382640(6) | 0.723254(4) | −1.20(6) | 0.2701(3) | 0.247(2) | 0.794(8) | 0.406(2) | 0.190(2) | 2.940(6) | 6.15(19) |
| 36 | 212808200 | 13.259 | 1.534780(5) | 0.651559(3) | −2.20(6) | 0.3152(15) | 0.159(3) | 0.928(23) | 0.513(5) | 0.340(5) | 2.489(14) | 5.27(30) |
| 37 | 212870977 | 14.714 | 1.971449(7) | 0.507241(3) | −1.15(6) | 0.2713(19) | 0.140(8) | 0.798(19) | 0.507(6) | 0.358(6) | 2.375(16) | 5.10(32) |
| 38 | 220277833 | 13.269 | 2.214118(6) | 0.451647(3) | −0.90(7) | 0.2998(2) | 0.134(3) | 0.839(22) | 0.470(6) | 0.347(5) | 2.290(15) | 4.83(31) |
| 39 | 220288040 | 14.083 | 1.842869(6) | 0.542632(3) | −1.40(6) | 0.2911(13) | 0.154(6) | 0.861(25) | 0.487(5) | 0.357(5) | 2.384(14) | 5.12(29) |
| 40 | 220435063 | 12.783 | 1.484671(6) | 0.673550(3) | −2.95(6) | 0.2844(14) | 0.146(2) | 0.815(10) | 0.440(5) | 0.351(5) | 2.385(15) | 5.01(30) |
| 41 | 220460648 | 17.193 | 1.715169(6) | 0.583033(4) | −2.05(7) | 0.2826(16) | 0.148(8) | 0.825(29) | 0.474(7) | 0.351(6) | 2.397(17) | 5.11(33) |
| 42 | 220489863 | 17.700 | 1.672909(5) | 0.597761(3) | −1.70(7) | 0.3223(17) | 0.147(4) | 0.955(22) | 0.498(6) | 0.355(6) | 2.406(16) | 5.15(32) |
| 43 | 220528452 | 17.651 | 1.795390(5) | 0.556982(3) | −1.10(7) | 0.2955(12) | 0.152(8) | 0.843(32) | 0.493(5) | 0.353(5) | 2.423(14) | 5.20(30) |
| 44 | 228881816 | 15.279 | 1.742731(6) | 0.573812(3) | −1.05(5) | 0.2881(11) | 0.167(7) | 0.847(20) | 0.498(5) | 0.333(5) | 2.515(13) | 5.37(29) |
| 45 | 228930895 | 16.177 | 1.711491(7) | 0.584286(4) | −1.75(5) | 0.2651(14) | 0.158(3) | 0.769(16) | 0.462(6) | 0.350(6) | 2.405(16) | 5.12(31) |
| 46 | 229105036 | 14.059 | 1.488529(5) | 0.671804(3) | −1.60(6) | 0.3249(14) | 0.167(2) | 0.954(22) | 0.530(5) | 0.339(5) | 2.681(13) | 5.47(29) |
| 47 | 246785473 | 13.367 | 1.631931(4) | 0.612771(2) | −1.25(7) | 0.3416(4) | 0.202(4) | 0.989(12) | 0.452(3) | 0.272(3) | 2.697(8) | 5.70(22) |
| 48 | 246872772 | 17.710 | 1.738429(7) | 0.575232(4) | −1.25(5) | 0.2197(9) | 0.165(3) | 0.608(15) | 0.447(4) | 0.333(4) | 2.388(12) | 5.05(27) |
| 49 | 248419289 | 15.718 | 1.606464(4) | 0.624485(3) | −1.35(6) | 0.3388(4) | 0.227(3) | 1.006(9) | 0.418(3) | 0.231(2) | 2.688(7) | 5.71(21) |
| 50 | 248419294 | 17.372 | 1.828708(6) | 0.546834(4) | −1.60(6) | 0.3537(12) | 0.148(12) | 1.050(18) | 0.487(7) | 0.363(7) | 2.344(18) | 4.99(34) |
| 51 | 248503821 | 16.175 | 1.649460(5) | 0.606259(3) | −1.35(7) | 0.3237(12) | 0.180(5) | 0.719(25) | 0.489(4) | 0.318(4) | 2.578(11) | 5.35(27) |
| 52 | 248529108 | 16.124 | 1.713629(6) | 0.583557(4) | −1.40(6) | 0.2377(8) | 0.182(7) | 0.674(12) | 0.503(4) | 0.308(3) | 2.638(9) | 5.58(25) |
| 53 | 248561687 | 17.956 | 1.825950(5) | 0.547660(2) | −2.80(6) | 0.3176(15) | 0.147(5) | 0.943(20) | 0.498(5) | 0.348(5) | 2.404(14) | 5.15(30) |
| 54 | 248565314 | 16.558 | 1.998968(4) | 0.500258(2) | −1.95(5) | 0.3503(17) | 0.141(4) | 1.030(34) | 0.485(6) | 0.359(5) | 2.344(15) | 5.02(30) |
| 55 | 248591089 | 15.554 | 1.873048(5) | 0.533889(2) | −1.30(7) | 0.3181(15) | 0.148(1) | 0.952(19) | 0.507(6) | 0.357(5) | 2.404(14) | 5.16(30) |
| 56 | 248828350 | 14.476 | 1.519119(5) | 0.658276(4) | −2.25(6) | 0.2925(14) | 0.152(5) | 0.860(20) | 0.479(5) | 0.355(5) | 2.421(14) | 5.16(29) |
| 57 | 251316614 | 15.626 | 2.197720(4) | 0.455017(1) | −1.30(6) | 0.4065(19) | 0.138(10) | 1.142(20) | 0.481(5) | 0.346(5) | 2.279(14) | 4.83(30) |
Note. (Column 1) No. of the star, (Column 2) ID of the target star, (Column 3) Kp magnitude, (Columns 4 and 5) pulsation frequency and corresponding period, (Column 6) metal abundance, (Column 7) the Fourier A1 coefficient, (Column 8) total amplitude, (Column 9) rise time (RT), and (Columns 10–13) Fourier-based coefficient.
3. Pulsation Analysis
Frequency analysis with Fourier decomposition is useful to characterize pulsations of RRLs (e.g., Simon & Teays 1982; Sandage 1993). For the non-Blazhko RRab stars, Nos. 8–57 in Table 1, a frequency analysis of the light curves is carried out with the software Period04. The corresponding uncertainties of the frequencies and periods are determined according to the method proposed by Zong et al. (2021). After the frequencies are extracted from the Fourier amplitude spectra, the light curves are fitted with the following formula concerning the sine function series:
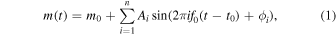
where n is the number of fitted orders, f0 is the main frequency, t is the observation time (Barycentric Julian Date: BJD-2454833.0) and t0 is the time of the first minimum apparent magnitude of the light curves. The mean magnitude m0, amplitude Ai , and phase ϕi values at the given ith order can be determined. As Simon & Lee (1981) suggested, certain combinations of Fourier coefficients are directly related to some of the physical parameters of pulsating stars. These coefficients are typically defined either as linear combinations of the phase difference of ϕij or as amplitude ratios Rij as follows:
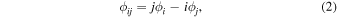
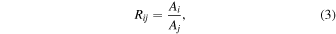
where i = 2 or 3, j = 1 for the fundamental modes of RRLs as suggested by Nemec et al. (2013) and Smolec et al. (2013). Note that ϕ21 and ϕ31 are corrected for integer multiples of π to meet the ϕ21 < π and π < ϕ31 < 2π conditions. The parameters of five Kepler RRab stars analyzed from Nos. 1–4 and No. 7 in Table 1 are taken from Nemec et al. (2011). We also calculated the maximum (Amax) and minimum (Amin) light with their corresponding phases ( and
and  ) of those stars in Kepler and K2 missions, by fitting a second- or third-degree polynomial around each peak and valley of the phase-folded light curves, which can be used to determine the rise time RT =
) of those stars in Kepler and K2 missions, by fitting a second- or third-degree polynomial around each peak and valley of the phase-folded light curves, which can be used to determine the rise time RT = 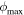 –
–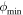 and total amplitude Atot = Amax–Amin for each star. The parameters of the stars KIC 9658012 and 9717032 denoted as Nos. 5 and 6 in Table 1 are determined in this work. The uncertainties of the Fourier coefficients for the 57 stars are also estimated. Table 1 lists the properties of these non-Blazhko RRLs in the fields of the LAMOST–Kepler/K2 survey.
and total amplitude Atot = Amax–Amin for each star. The parameters of the stars KIC 9658012 and 9717032 denoted as Nos. 5 and 6 in Table 1 are determined in this work. The uncertainties of the Fourier coefficients for the 57 stars are also estimated. Table 1 lists the properties of these non-Blazhko RRLs in the fields of the LAMOST–Kepler/K2 survey.
4. Results of the Analysis
4.1. Properties of Fourier Composition Coefficients
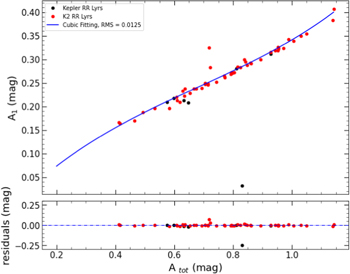
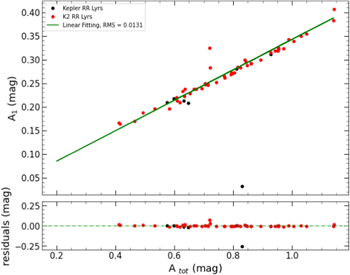
The Fourier coefficient of A1 is approximately proportional to the total amplitude of Atot, since it is the dominant component of Atot. In order to illustrate this relationship between A1 and Atot, we use a cubic and a linear equation to fit the two coefficients A1 and Atot following Nemec et al. (2011), who found that the dependence between the two coefficients might be cubic using the 19 non-Blazhko RRab stars observed by Kepler, and Skarka (2014), who analyzed 176 non-Blazhko RRab stars from ASAS and WASP surveys found that the relation might be linear for the two coefficients, respectively. The cubic fitting is as follows:
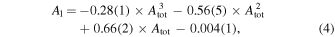
while the linear fitting is as follows:
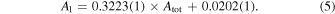
When the cubic curve (as shown in the top panel of Figure 3) is subtracted from the Atot–A1 diagram, the residuals show no significant deviations from the average value of zero with the rms of 0.0125 mag (as shown in the bottom panel of Figure 3). But for the linear fitting, although the residuals show no significant variations (presented in the bottom panel of Figure 4) after subtracting the linear trending (presented in the top panel of Figure 4) from the Atot–A1 diagram, the value of the rms is 0.013 mag, which is slightly larger than that of the cubic fitting. It is worth mentioning that the data points away from 3σ are not considered for these two kinds of fittings as shown in the top panels of the two figures.
Figure 3. The relationship between Atot and A1. The black and red dots denote the RRLs in this study observed by Kepler and K2, respectively. The blue curve of the data points is shown in the top panel, and the bottom panel shows the residuals.
Download figure:
Standard image High-resolution imageFigure 4. The relationship between Atot and A1. The black and red dots denote the RRLs in this study observed by Kepler and K2, respectively. The green line denotes the linear fitting of the data points as shown in the top panel, and the bottom panel shows the residuals.
Download figure:
Standard image High-resolution imageSkarka (2014) and Nemec et al. (2011) investigated the relation between the two Fourier coefficients ϕ21 and ϕ31 of the non-Blazhko RRab stars, and they both pointed out that the two coefficients of the stars follow a linear relation. In this work, we perform a linear fitting for the two Fourier coefficients ϕ21 and ϕ31 and the fitting equation is as follows:
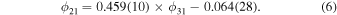
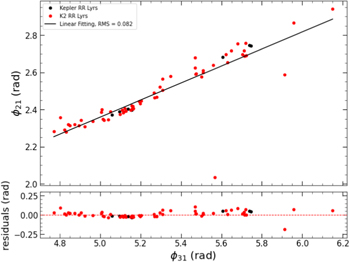
The fitting is shown in the top panel of Figure 5, and the residuals are plotted in the bottom panel of the figure, with an rms of 0.082 rad. The data points beyond 3σ away from the trending are not considered in the fitting.
Figure 5. The relationship of ϕ31 and ϕ21. The black and red dots represent RRLs in this study in the Kepler and K2 fields, respectively. The dark line represents the linear equation between the two coefficients with an rms of 0.082 rad as shown in the top panel. After extracting this fit, the residuals are shown in the bottom panel.
Download figure:
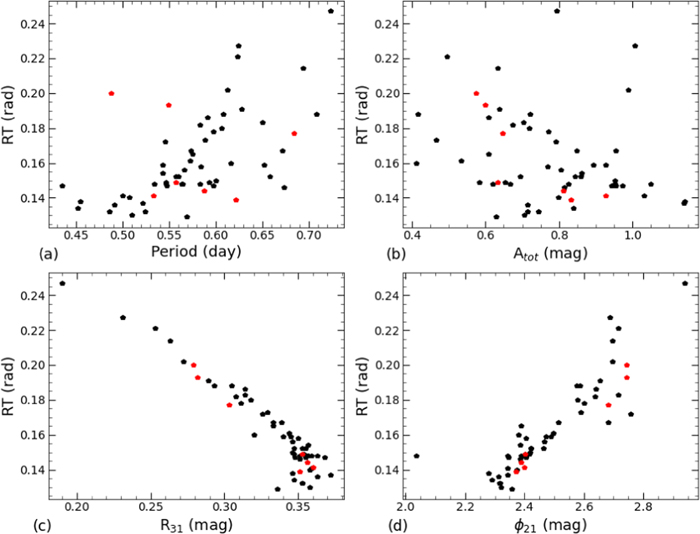
Standard image High-resolution imageFigure 6 shows how the RT correlates with the parameters of the light curves, including the fundamental period, total amplitude Atot, the amplitude ratio R31, and the phase difference ϕ21. Panel (a) shows the relationship between the RT and the main pulsation period. It can be seen that the longer period probably corresponds to a higher RT for most of the stars. This is the first time that this tendency is noticed for Kepler and K2 non-Blazhko RRab stars. The data points of the total amplitudes Atot versus RT are scattered as shown in panel (b). R31 and RT might follow a roughly linear trend as shown in panel (c). The distribution of RT versus ϕ21 is scattered as shown in panel (d).
Figure 6. RT as a function of the parameters of the light curves. The non-Blazhko RRab stars in this study observed by Kepler and K2 are represented by red and black dots, respectively.
Download figure:
Standard image High-resolution image4.2. Period–ϕ31–[Fe/H] Relation
A series of studies (Jurcsik & Kovacs 1996; Kovacs & Jurcsik 1996; Kovács & Walker 2001; Jurcsik et al. 2009; Nemec et al. 2013; Ngeow et al. 2016; Plachy et al. 2016; Iorio & Belokurov 2021; Mullen et al. 2021) have been conducted to investigate the period–ϕ31–[Fe/H] relation. In this study, we use the fundamental periods P and the phase differences ϕ31 of the 54 non-Blazhko RRab stars with the metal abundances [Fe/H] of these stars provided by the LAMOST–Kepler/K2 survey to give a new calibration of the relation. This relation can be fitted by the following equation:
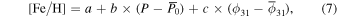
where 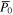 and
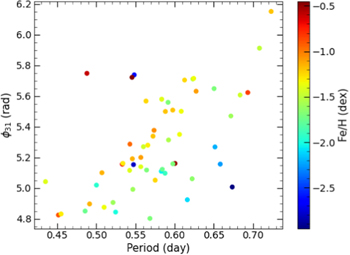
and 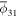 are the mean values of the fundamental periods and phase differences ϕ31 of the 54 non-Blazhko stars studied in this work, respectively. We adopt the least squares method, which is implemented by the SciPy package (Virtanen et al. 2020) to estimate the best-fitting coefficients with their corresponding standard errors, for which a = −3.650 (1), b = 0.848 (4), and c = −3.992 (1). Figure 7 illustrates the distribution of the [Fe/H] in the ϕ31 versus the plane of the period of those RRLs.
are the mean values of the fundamental periods and phase differences ϕ31 of the 54 non-Blazhko stars studied in this work, respectively. We adopt the least squares method, which is implemented by the SciPy package (Virtanen et al. 2020) to estimate the best-fitting coefficients with their corresponding standard errors, for which a = −3.650 (1), b = 0.848 (4), and c = −3.992 (1). Figure 7 illustrates the distribution of the [Fe/H] in the ϕ31 versus the plane of the period of those RRLs.
Figure 7. Period–ϕ31–[Fe/H] fit for the RRLs observed in the LAMOST–Kepler/K2 survey. The color bar is the value of the period.
Download figure:
Standard image High-resolution image5. Discussion
5.1. Properties of the Fourier Composition Coefficients
In this study, we find that the values of standard errors of cubic fit and linear fit for the relation of the amplitude of the primary frequency A1 and the total amplitude Atot of the 54 non-Blazhko RRab stars are σ1 = 0.013 and σ2 = 0.0125, respectively, which means that they follow either a cubic or linear relation. We do not find any relation for RT with the fundamental period, total amplitude Atot, and phase difference ϕ21 of the stars studied in this work. However, Skarka (2014) suggested that the RT follows a linear relation with those parameters for the non-Blazhko RRab stars but does not for the Blazhko RRab stars, which is not consistent with our result. This might be due to that the precision of the photometry from Kepler and K2 is much higher than that of the photometric data in the previous study. As far as the relation between ϕ21 and ϕ31 of the stars, we find that they follow a linear relation. But Skarka (2014) found that the dependence of the two coefficients of ϕ21 and ϕ31 is not very strong.
5.2. Comparison of RRab Stars in GCs and the Large Magellanic Cloud Field
As the Fourier decomposition coefficients were derived from light curves observed in the Kepler white band of the 54 non-Blazhko RRab, we convert them into V mag using formula (2) of Nemec et al. (2011). Figure 8 shows the correlations of properties of the non-Blazhko RRab stars in this study with the 177 RRab stars located in several Galactic and Large Magellanic Cloud (LMC) GCs (Kovács & Walker 2001). Panel (a) shows the logP–ϕ31 diagram. The stars in the GCs with poor and intermediate metallicities clearly define two edges, respectively. The metal-poor subsample consists of 19 stars, whose metallicities are in the range of −1.70 to −1.99 dex with an average value of −1.8 dex (Kovács & Walker 2001; Nemec et al. 2011). The other subsample stars are the intermediate-metallicity stars containing 39 members, whose metallicities are between −0.97 and −1.23 dex with an average value of −1.1 dex. It is clear that most non-Blazhko RRab stars in the LAMOST–Kepler/K2 fields have metal abundances between −1.80 and −1.10 dex, except for two Kepler stars and five K2 stars with metallicities higher than −1.1 dex. Panel (b) shows that the distribution of the Fourier coefficients R21 and R31 of the 54 non-Blazhko RRab stars in the Kepler/K2 survey are similar to the RRab stars in GCs. For the stars studied in this work, we find that some of them with low R31 values have relatively high R21 values. We also find that most stars appear in the upper right-hand side of panel (b) and most of them have high metallicities. Panel (c) shows that the stars studied in this work do not differ from the stars in GCs. We also note that the metallicities may not show any significant effect in this panel. Panel (d) shows the agreement between the phase parameters of the 54 non-Blazhko RRab stars and GC RRab stars, which supports that the phase parameters of 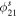 and
and 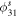 might follow a linear relation. However, panel (d) also demonstrates very little dependence on the metallicities.
might follow a linear relation. However, panel (d) also demonstrates very little dependence on the metallicities.
Figure 8. Correlation of properties of LAMOST–Kepler/K2 non-Blazhko RRab stars with the 177 RRab stars located in several Galactic and LMC GCs (black small dots ). The cluster RRab stars presented here are taken from Kovács & Walker (2001), which were adopted by Nemec et al. (2011). The green and yellow triangles represent the stars in the Kepler and K2 fields in this study, respectively. The 19 most metal-poor stars, whose metallicities are between −1.70 and −1.99 dex with a mean value of −1.80 dex, are marked by blue circles. The 39 most metal-rich stars, whose metallicities are in the range of −0.97 to −1.23 dex with a mean value of −1.10 dex, are marked by red circles. The blue and red lines in panel (a) denote the linear fitting for the metal-poor and intermediate metal-abundance stars, respectively. Note that the superscripts “S” and “C” of the coefficients signify phase parameters computed with sine and cosine series, respectively.
Download figure:
Standard image High-resolution imageAs the cluster RRLs adopted in this work cover roughly 1 dex in the intermediate metal regime, we collected the data of the reference stars from a large sample of high-resolution spectroscopic surveys of RRLs (For 2011; Nemec et al. 2013; Govea et al. 2014; Chadid et al. 2017; Sneden et al. 2017; Magurno et al. 2019; Crestani et al. 2021; Gilligan et al. 2021), with the metallicities of RRLs ranging from −3.0 dex to solar or super-solar iron abundance based on those high-resolution spectra. We cross match the catalog of those studies with our data for the reference stars. We derived seven common stars from the study of Nemec et al. (2013) but no common stars from other literature (For 2011; Govea et al. 2014; Chadid et al. 2017; Sneden et al. 2017; Magurno et al. 2019; Crestani et al. 2021; Gilligan et al. 2021) and those stars are all in the Kepler field. But we note that our database of the metallicities of RRLs studied in this work is a subsample of Liu et al. (2020), who collected the data of the reference stars with reliable estimates of metallicity either from high-resolution spectroscopy with the metallicity in the range of −2.95 to −0.59 dex (Clementini et al. 1995; For 2011; Kinman et al. 2012; Nemec et al. 2013; Govea et al. 2014; Pancino et al. 2015) or as a member star of GCs (Harris 2010) in the metallicity range of −2.37 to −1.29 dex. They finally obtained 47 stars in common, which formed their reference star sample. The scale of metallicity adopted by them was the one established by Carretta et al. (2009), which was derived from the old scale of metallicity (Zinn & West 1984). They found that the values of metallicities of RRLs estimated from the low-resolution spectra of LAMOST DR6 agree well with those of the compiled reference stars, with a negligible offset of -0.04 dex and a standard deviation of 0.22 dex. They also found that the dispersion is comparable to that yielded by multi-epoch observations.
We also compare the Fourier decomposition coefficients R21, R31, 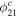 , and
, and 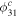 with those derived for the RRLs in the central regions of the LMC. The latter is determined from the OGLE Collection of Variable Stars by Soszyński et al. (2016) and transformed from the I to V band using equations provided by Morgan et al. (1998). It is clear that the coefficients of the 54 non-Blazhko RRab stars determined in this work agree with the coefficients of the RRab stars well and differ from other types of RRLs a s shown in Figure 9.
with those derived for the RRLs in the central regions of the LMC. The latter is determined from the OGLE Collection of Variable Stars by Soszyński et al. (2016) and transformed from the I to V band using equations provided by Morgan et al. (1998). It is clear that the coefficients of the 54 non-Blazhko RRab stars determined in this work agree with the coefficients of the RRab stars well and differ from other types of RRLs a s shown in Figure 9.
Figure 9. Comparison of Fourier coefficients of the non-Blazhko RRab stars in this study with those derived from the OGLE-IV LMC field RRLs provided by Soszyński et al. (2016) and the known non-Blazhko RRab stars observed by Kepler and determined by Nemec et al. (2011). The red points represent RRab, green points RRc stars. The blue pentagons denote stars observed by both Kepler and LAMOST DR6. The black pentagons denote the stars observed by both K2 and LAMOST DR6.
Download figure:
Standard image High-resolution image5.3. Period–ϕ31–[Fe/H] Relation
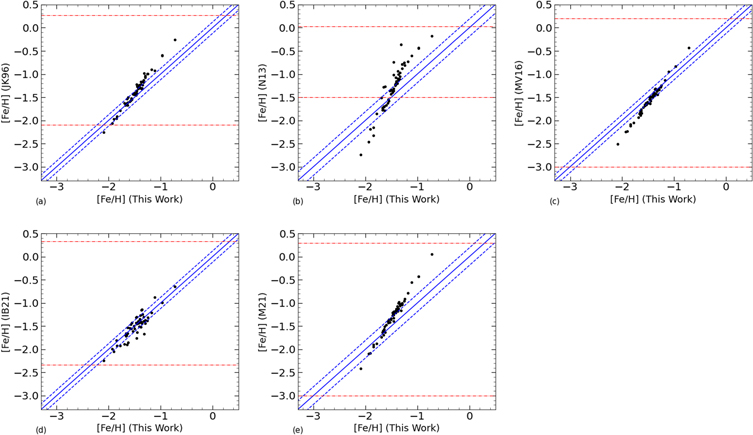
We compare the metallicities [Fe/H] of the stars studied in this work calculated using Equation (7) with those derived by relationships as documented in the literature (Jurcsik & Kovacs 1996; Nemec et al. 2013; Martinez-Vazquez et al. 2016; Iorio & Belokurov 2021; Mullen et al. 2021). For consistency, the metallicities of those investigations are converted to the often-used scale of Carretta et al. (2009). The result of this comparison is shown in Figure 10; the abscissa of all subgraphs refers to the metallicities of the stars calculated using Equation (7), and the ordinate of all subgraphs refers to the metallicities of the stars derived with the relations in the literature. Panel (a) shows a comparison of the metallicities between ours and those of Jurcsik & Kovacs (1996), whose relation was derived using photometric data of 81 RRab field stars in the V band with metallicities based on the high-dispersion spectroscopy scale of Jurcsik (1995). For consistency, we first convert the metallicities derived with their relation to the Carretta et al. (2009) scale using the formula provided by Kollath et al. (2011): [Fe/H]C09 = 1.001[Fe/H]JK96 −0.112. We then convert the Fourier coefficient ϕ31 in the K p system to the V band with formula (2) of Nemec et al. (2011). We find that the comparing result between the two relations is obviously different within the calibration range of (−2.1 dex ≤ [Fe/H] ≤ 0.7 dex) of Jurcsik & Kovacs (1996) (red horizontal lines), particularly in the metal-rich regime. This might be due to that the photometric data of Jurcsik & Kovacs (1996) were collected from heterogeneous observations at various sites and either lacked phase coverage or had excessive noise that caused a failure of the Fourier fit in Jurcsik & Kovacs (1996). Nemec et al. (2013) derived a quadratic period–ϕ31–[Fe/H] relation using 19 RRab stars in the Kepler field with accurate metallicities measurements. The comparison of the metallicities between ours and those of Nemec et al. (2013) is shown in panel (b). The Fourier coefficients ϕ31 of the 57 stars are in the same K p system as that of Nemec et al. (2013). Furthermore, the scale of metallicity adopted by Nemec et al. (2011) and ours is of the same scale as that in Carretta et al. (2009). Note that the scatter is obviously large for either the higher metallicity or lower metallicity in their range (−1.5 dex ≤ [Fe/H] ≤ 0.03 dex). Mullen et al. (2021) suggested that this might be caused by the higher-order term of the relationship given by Nemec et al. (2013), and they had only one RRab star with [Fe/H] ≤ −2.0 dex resulting in the scarcity of calibrators in their sample for low [Fe/H]. Martinez-Vazquez et al. (2016) gave a new calibration of the period–ϕ31–[Fe/H] relation based on a sample of 381 RRab stars in the GCs and eight RRab field stars in order to extend the metallicities range of their samples. The metallicities of their sample were on the Carretta et al. (2009) scale, and we also convert the K p system ϕ31 value to the V-band system using formula (2) in Nemec et al. (2011). Our metallicities compared with those of Martinez-Vazquez et al. (2016) show an obvious scatter within the entire calibration range in Martinez-Vazquez et al. (2016), as presented in panel (c). This phenomenon might be due to that the sample of 381 RRab stars was binned by period; they computed the mean period, ϕ31, and V-band amplitude, which means that the calibration provided by Martinez-Vazquez et al. (2016) was based on the average instead of the individual properties. Iorio & Belokurov (2021) derived a G-band period–ϕ31–[Fe/H] relation based on the light curves of 84 RRab stars in Gaia DR2 with known spectroscopic metallicities. For this comparison, we first use formula (2) of Kollath et al. (2011) to convert the ϕ31 value in the Kp system to the V-band system, then convert it to that in the G-band system using formula (6) of Clementini et al. (2016). What is more, an additional π offset should be subtracted from ϕ31 to set the coefficients on the same scale as Iorio & Belokurov (2021) as suggested by Mullen et al. (2021). However, the metallicity abundances adopted by Iorio & Belokurov (2021) were on the scale used in Zinn & West (1984). We convert the metallicity abundances of Iorio & Belokurov (2021) to the Carretta et al. (2009) scale using the formula [Fe/H]C09 =1.105[Fe/H]ZW84 + 0.160. The comparison of the metallicities between ours and those of Iorio & Belokurov (2021) exhibit a general agreement within the entire range of metallicity (−2.53 dex ≤ [Fe/H] ≤ 0.33 dex), with an rms of 0.123 dex, as shown in panel (d). However, Mullen et al. (2021) pointed out that the relation given by Iorio & Belokurov (2021) tends to overestimate the metallicity at the metal-poor end and underestimate the metallicity at the metal-rich end. Panel (e) shows the comparison of metallicities between ours and those of Mullen et al. (2021), who used 1980 RRab stars with metallicity in the range of −3.0 dex ≤ [Fe/H] ≤ 0.4 dex. We first convert the ϕ31 value in the Kp system to the V-band system using formula (2) in Nemec et al. (2011). A small shift of 0.08 dex is considered in converting to the often-used Carretta et al. (2009) scale of [Fe/H] as suggested by Mullen et al. (2021). The result exhibits an obvious scatter between the two relations for the entire range of metallicities. This might be due to that the sample of RRab stars in Mullen et al. (2021) is significantly larger than ours.
Figure 10. Comparison of the [Fe/H] values of the non-Blazhko RRab stars in Table 1 derived by Equation (7) with those obtained from the relationship in Jurcsik & Kovacs (1996), Nemec et al. (2013), Martinez-Vazquez et al. (2016), Iorio & Belokurov (2021), and Mullen et al. (2021), respectively. The blue solid lines denote 1:1 secants, and the blue dashed lines denote the 1σ dispersions of those differences in the metallicity derived by the equation in the literature and ours. The range of calibrated metallicities used in each work to derive their respective relations are noted in each panel with red dashed–dotted lines.
Download figure:
Standard image High-resolution image6. Conclusions
After cross matching the target stars of Kepler and K2 photometry with those of the spectroscopic observations in LAMSOT DR6, we derived a sample of 57 non-Blazhko RRab stars. The pulsation periods of these stars are determined with the Fourier decomposition method applied to the light curves, including R21, R31, ϕ21, ϕ31, A1, and Atot. We find that the amplitude ratios R21, R31, and the phase differences ϕ21 and ϕ31 are consistent with those determined in GCs and the LMC. There is a linear relationship between the phase differences of ϕ21 and ϕ31, which agrees well with those in the literature (Skarka 2014). In terms of the amplitudes of the stars studied in this work, we suggest that the amplitudes of primary frequencies A1 and the total amplitudes Atot follow either a cubic or linear pattern, and need to be investigated in the future. For the RT, we do not find its relevance with the fundamental pulsation period, Atot and ϕ21. However, it might follow a linear relationship with R31.
Based on the homogeneous metallicities, we derived a new calibration formula for the period–ϕ31–[Fe/H] relation, which agrees well with those in previous studies as documented in the literature (Jurcsik & Kovacs 1996; Nemec et al. 2013; Martinez-Vazquez et al. 2016; Iorio & Belokurov 2021; Mullen et al. 2021). We foresee a much larger catalog to be coming as LAMOST is ongoing to release spectra both in low resolution and medium resolution for targets with Kepler and K2 photometry (Fu et al. 2020). A more in-depth and larger catalog could refine the calibration of such relationships between different pulsation parameters. Those observational results might bring new constraints to the hydrodynamic models constructed for RRLs in general.
We acknowledge the support from the National Natural Science Foundation of China (NSFC) through grants 11833002, 12090040, 12090042, 12273002, and 12203010. W.Z. is supported by the Fundamental Research Funds for the Central Universities. The Guoshoujing Telescope (LAMOST) is a National Major Scientific Project built by the Chinese Academy of Sciences. The authors gratefully acknowledge the Kepler team and all who have contributed to making this mission possible.
Software: astropy (Astropy Collaboration et al. 2013; Astropy Collaboration (2018), LightKurve (Vinícius et al. 2018; Barentsen et al. 2021), Period04 (Lenz & Breger 2005).