Abstract
Hydrogen emissions of RR Lyrae variables are the imprints of shock waves traveling through their atmospheres. We develop a pattern recognition algorithm, which is then applied to single-epoch spectra of the Sloan Digital Sky Survey and the Large Sky Area Multi-Object Fiber Spectroscopic Telescope survey. These two spectroscopic surveys covered ∼10,000 photometrically confirmed RR Lyrae stars. We discovered in total 127 RR Lyrae stars with blueshifted Balmer emission features, including 103 fundamental mode (RRab), 20 first-overtone (RRc), 3 double-mode (RRd), and 1 Blazhko-type (temporary classification for RR Lyrae stars with strong Blazhko modulation in the Catalina sky survey that cannot be characterized) RR Lyrae variable. This forms the largest database to date of the properties of hydrogen emission in RR Lyrae variables. Based on Zwicky Transient Facility DR5, we carried out a detailed light-curve analysis for the Blazhko-type RR Lyrae star with hydrogen emission of long-term modulations. We characterize the Blazhko-type RR Lyrae star as an RRab and point out a possible Blazhko period. Finally, we set up simulations on mock spectra to test the performance of our algorithm and on the real observational strategy to investigate the occurrence of the “first apparition.”
1. Introduction
RR Lyrae stars are Population II stars commonly found in globular clusters. They are located at the intersection of the instability strip and the horizontal branch (HB), from A to F type (Smith 1995; Sesar 2012). RR Lyrae variables are classified, according to the number of oscillation modes, as fundamental mode (RRab), the first-overtone mode (RRc), or double-mode (RRd) stars (Soszyński et al. 2011). They obey the MV –[Fe/H] relation (Muraveva et al. 2018) and the period–luminosity–metallicity relationship (Longmore et al. 1986; Catelan et al. 2004) in the infrared passbands, which makes them good “standard candles” for precise distance determinations for star clusters and nearby galaxies (Bhardwaj 2020). Some of the RR Lyrae variables, across all subtypes, show periodic amplitude and/or phase modulations, which is known as the “Blazhko effect” (Blažko 1907; Kolenberg et al. 2006).
Despite the successful application of RR Lyrae stars as a step of the distance ladder, the detailed dynamical evolutions of the interior are unclear and complicated. However, we can speculate on the internal structure of RR Lyrae variables by tracing the imprints of feature lines on spectra. Hydrogen emission lines, helium emission lines, line broadening and doubling phenomena, and neutral metallic line disappearance phenomena in RR Lyrae stars indicate shock waves propagating through their atmospheres (Chadid et al. 2008, 2017). The emissions are produced when atoms in the gas de-excite after being excited by a shock wave traveling into the atmosphere. The shock provides high enough energy to excite neutral hydrogen from the second quantum state upward. It compresses, heats, and accelerates the gas. After that, the atoms release energy in the cooler shock wake region and generate the emission (Gillet & Fokin 2014).
Hydrogen emission lines of RR Lyrae stars are called “apparitions” (Preston 2011). There are three famous “apparitions,” which got their sequence number based on the discovery time. Sanford (1949) first reported a hydrogen emission in RR Lyrae in 1949. The “first apparition” is an intense blueshifted emission, which mostly presents during ϕ ≈ 0.91 (in RRab), just before the maximum luminosity (Gillet et al. 2019). Duan et al. (2021) reported the first detection of blueshifted hydrogen emission (the “first apparition” at both Hα and Hβ) in the first-overtone and double-mode RR Lyrae variables. Now it is well accepted that the “first apparition” is generated from the hot emitting layer behind an outward-moving shock front (Schwarzschild 1952).
The “second apparition” is a weak hump at the blue side of the absorption-line wing, when ϕ ≈ 0.73, discovered in 1988 (Gillet & Crowe 1988). It is generated by the collision when layers of the upper atmosphere meet the photospheric layers during the infalling processes of the ballistic motion. It occurs during the small bump around ϕ ≈ 0.72, which was produced by the “early shock” (Hill 1972; Gillet & Fokin 2014). Moreover, the third one was discovered in 2011 (Preston 2011), which is a weak redshifted emission line that appears at around ϕ ≈ 0.30. There are two views on the origin of the “third apparition.” One is that it is possibly provided by a weakly supersonic and post-maximum infalling shock wave (called ShPM), which is generated from superimposing compression due to the hydrogen recombination front and the accumulation of weak compression waves (Chadid & Preston 2013). The other opinion is that this emission is a P-Cygni−like profile, which is the sign that the envelope surrounding the stellar surface is expanding, and the emission was produced when the shock wave is detached from the photosphere. To confirm which one is closer to the fact, further investigation is still needed.
Thanks to the rapid improvement of observing facilities, we can get an ever-expanding volume of observed spectroscopic data of RR Lyrae variables. In this work, we develop a pattern recognition searching algorithm and apply it to a large database of single-epoch spectra, the “first apparition.” We find spectra of RR Lyrae stars that show the most prominent observational characteristics of shock waves. We report hydrogen emissions in 103 RRab, 20 RRc, 3 RRd, and 1 Blazhko-type RR Lyrae variable. 7 The detection of blueshifted hydrogen emission in nonfundamental mode RR Lyrae variables has been discussed in our previous work (Duan et al. 2021). In this work, we present the results of RRab variables and the Blazhko-type RR Lyrae stars (RR-Bl, the Blazhko-type RR Lyrae star with Large Sky Area Multi-Object Fiber Spectroscopic Telescope survey (LAMOST) spectra and hydrogen emission). The Blazhko-type RR Lyrae star is characterized as an RRab pulsator using the pre-whitening sequence method. We build up the largest database of properties of the “first apparitions” in RR Lyrae stars based on the Sloan Digital Sky Survey (SDSS) and LAMOST, to investigate shock waves in RR Lyrae stars with a new view.
This paper is organized as follows. In Section 2, we describe the observations of both photometry and spectroscopy. The searching methods are interpreted in Section 3. We display the results of the search in Section 4. Moreover, we analyze the frequency components in RR-Bl, characterize it as an RRab star, and provide a possible Blazhko period in Section 5. The detection rate and mock spectra test are discussed in Section 6. Finally, the conclusions are covered in Section 7.
2. Observations
2.1. Photometric Observations
Both photometric and spectroscopic observations are needed to hunt for the “first apparitions.” Light curves are used to identify RR Lyrae variables. They can be collected from the Catalina Sky Surveys, the Wide-field Infrared Survey Explorer (WISE), the All-Sky Automated Survey for Supernovae (ASAS-SN), and the Asteroid Terrestrial-impact Last Alert System (ATLAS).
The Catalina Sky Survey began in 2004 (Drake et al. 2009). It uses three telescopes to cover the sky (−75° < δ < +65°), in order to search for near-Earth objects (NEOs) and potential hazardous asteroids (PHAs). The subsurveys are specified as the Catalina Schmidt Survey (CSS); the Mount Lemmon Survey (MLS), located in Tucson, Arizona; and the Siding Spring Survey (SSS), which is located in Siding Spring Australia. In the Catalina survey, RR Lyrae stars with strong Blazhko modulation are classified as “Blazhko-type” rather than the basic types (RRab, RRc, and RRd) of RR Lyrae variables, because the long-term modulation strongly influences the classification. Lots of photometric observations and analyses of RR Lyrae stars have been provided by related works (Drake et al. 2013a, 2013b, 2014, 2017; Torrealba et al. 2015).
Moreover, WISE (Chen et al. 2018) is a 40 cm space telescope, designed to implement an all-sky survey in four mid-IR bands, including W1 (3.35 μm), W2 (4.60 μm), W3 (11.56 μm), and W4 (22.09 μm) (Wright et al. 2010). Chen et al. (2018) have compiled the first all-sky mid-IR variable-star catalog based on WISE 5 yr survey data, providing 1231 newly identified RR Lyrae stars.
ASAS-SN (Shappee et al. 2014; Kochanek et al. 2017) currently consists of 24 telescopes around the globe. It is now automatically surveying the entire visible sky every night down to ∼18 mag. The catalog from ASAS-SN (Jayasinghe et al. 2019) provides ∼412,000 variables, including ∼8000 periodic pulsating stars.
The Asteroid Terrestrial-impact Last Alert System (ATLAS; Heinze et al. 2018) scans most of the sky every night to search for dangerous asteroids, which is also used to search for photometric variability (Tonry et al. 2018). We also get light curves from the Zwicky Transient Facility (ZTF; Bellm et al. 2019; Masci et al. 2019; Chen et al. 2020) and parameters from Gaia DR2 (Clementini et al. 2019) for our selected stars if available.
2.2. Spectroscopic Observations
Our spectroscopic data were collected from SDSS and LAMOST. In this work, we adopt low-resolution and single-epoch spectra. The periods of RR Lyrae stars are very short. Under the circumstances, the emission features can be overwhelmed by long-time exposures and the processes of combining spectra to get a higher signal-to-noise ratio (S/N). Therefore, we use low-resolution and single-epoch spectra to capture these features, which will quickly wear away otherwise.
SDSS (Eisenstein et al. 2011) is one of the most ambitious surveys in the history of astronomy and enjoys enormous influence. It saw its first light in 1998 and entered routine observations in 2000. Using the Sloan Foundation 2.5 m optical telescope (Apache Point Observatory, New Mexico), SDSS serves images and spectra of the northern sky, and it currently extends to the southern sky using the 2.5 m Du Pont optical telescope (Las Campanas Observatory, Chile). SDSS-III is a massive spectroscopic survey focusing on the distant universe, the Milky Way, and extrasolar planetary systems (Eisenstein et al. 2011). For the SDSS data set, some of the spectra come from the Baryon Oscillation Spectroscopic Survey (BOSS; Dawson et al. 2013). Spectra from SDSS cover wavelengths from 3800 to 9200 Å, and those from BOSS have wavelength coverage of 3650–10400 Å. They achieve R ∼ 1500 at 3800 Å and R ∼ 2500 at 9000 Å. In this work, we use SDSS DR9 because we utilize parameters from the SEGUE Stellar Parameter Pipeline (SSPP; Lee et al. 2008).
LAMOST (Cui et al. 2012; Deng et al. 2012; Zhao et al. 2012) is a Chinese national scientific research facility. This survey consists of two major parts: the LAMOST ExtraGAlactic Survey (LEGAS) and the LAMOST Experiment for Galactic Understanding and Exploration (LEGUE). It sets up a spectroscopic survey of millions of objects in much of the northern sky and has great potential to survey a large volume of space efficiently. We apply for low-resolution and single-exposure spectra in LAMOST DR6 (R ∼ 1800). Each plate was observed more than 3 times for SDSS and 1–3 times for LAMOST. For SDSS, the exposure time is 10–40 minutes each; for LAMOST, it is 10–30 minutes each. This provides the finest time resolution for RR Lyrae targets.
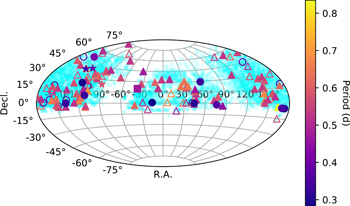
From this large database, we can screen out spectra of RR Lyrae stars. We cross-match the catalog of RR Lyrae stars and the data set of spectra with TOPCAT (Taylor 2005) and apply for single-epoch spectra from LAMOST. We get single-epoch spectra of 3526 RR Lyrae stars from SDSS DR9 and 5571 RR Lyrae stars from LAMOST DR1-6. The locations of RR Lyrae stars of this sample are shown in Figure 1.
Figure 1. Spatial distribution of selected targets with the “first apparition,” with the color denoting the value of period. Corresponding relation: open triangle—RRab from SDSS; filled triangle—RRab from LAMOST; open circle—RRc from SDSS; filled circle—RRc from LAMOST; star—RRc from LAMOST; square—one Blazhko-type star in LAMOST. Light-blue points in the background denote the whole sample that our survey is based on.
Download figure:
Standard image High-resolution image3. Methods
Based on the profiles of the “first apparitions,” we adapt two methods to search for this kind of feature. In this section, we will explain the technical details of the pipeline we use to catch the blueshifted hydrogen emission lines of RR Lyrae stars in a large sky survey database.
3.1. 1D Pattern Recognition Method
The normal practice to search for a target feature is to check the profiles of spectra visually. Due to rapid growth of data sets in size and complexity, data science is being introduced into astronomical studies (Pesenson et al. 2010; Baron 2019). Pattern recognition means automated recognition of patterns and regularities in data. It has become a useful tool in fetching specific features and dealing with classification (Djorgovski et al. 2006).
Given that the profile we want is quite simple and clear, we adopt a 1D pattern recognition method with handcrafted rules. We can trace the trend of the profile as an intense emission Gaussian-like profile at the shoulder of the blue wing of a Gaussian-like absorption-line wing. Both emission and absorption signatures should be more significant than 2σ.
We choose windows of 6540–6590 Å for Hα and 4840–4880 Å for Hβ. We presuppose that the minimum values in the selected windows indicate the location of Balmer absorption profiles. The adopted results at least show clear target patterns at Hα and Hβ simultaneously. Both emission and absorption components should contain at least two observational points. We apply the pipeline to our collected spectra sample, with visual checks to avoid a false negative.
3.2. Cross-correlation Method
Given that the appearance of the emission lines introduces a sudden change on the spectra, the cross-correlation method is also useful for selecting blueshifted hydrogen emissions (Yang et al. 2014). If there is not a “first apparition,” there should only be one wide absorption line of Hα on the spectrum. On the contrary, there would be one additional emission line, which introduces a big difference in the shapes of two spectra. So if the difference between radial velocities is strangely large, there are possibly the “first apparitions.”
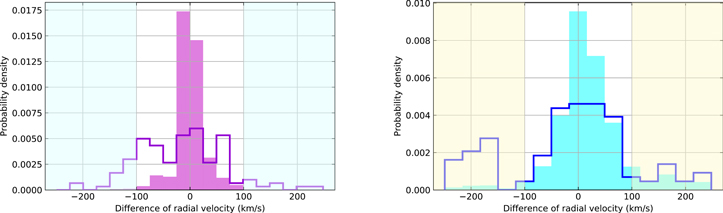
The cross-correlation method implemented here works as follows: We use the first observed spectrum in a pair as the template, while the second one is shifted by 1 km s−1 steps between −250 and 250 km s−1. The shifted template is linearly interpolated at the points of the wavelength of the observational spectrum to calculate the cross-correlation function. This shows the difference of radial velocities (ΔRV) between two spectra when the cross-correlation function reaches its maximum. Here we provide the results of differences of radial velocities with the Hα line in Figure 2.
Figure 2. Distribution of the differences of radial velocities for SDSS (left) and LAMOST (right). The data set was cleaned by S/N ≥ 15 and 3σ criteria. The filled histogram denotes the whole sample. The open histogram represents the distribution of the differences of radial velocities for the selected stars in this work. For the cross-correlation method, we try to seek the “first apparition” when ∣ΔRV∣ > 100 km s−1.
Download figure:
Standard image High-resolution imageWe locally normalize the spectra between 6540 Å < λ < 6590 Å by the fitting result of the continuum. The quantity σ of the spectra is calculated from the rms of the spectra from the first and last five points, within which the spectra are continuum dominated. We adopted results with both spectra satisfying S/N > 15, and the significance of the absorption line is over 3σ. The distributions of ΔRV for both the SDSS and LAMOST data sets are visualized in Figure 2. We check for the blueshifted hydrogen emission when ∣ΔRV∣ > 150 km s−1.
All of the selected results are produced by the 1D pattern recognition pipeline. The cross-correlation method provides 13 RRab stars and 1 RRc star for SDSS and 44 RRab stars, 3 RRc stars, 1 RRd star, and 1 Blazhko-type RR Lyrae star for LAMOST. The distributions of ΔRV for selected RR Lyrae stars are visualized in Figure 2. The cross-correlation method does help, but not all of the spectra with emission show high ΔRV, and not all spectra with high ΔRV show emission. So our work is mainly based on the 1D pattern recognition pipeline. The cross-correlation method is used as a supplement.
4. Results
As a result, we find 33 RRab stars and 10 RRc stars in SDSS and 70 RRab stars, 10 RRc stars, 3 RRd stars, and 1 Blazhko-type RR Lyrae star in LAMOST that show the “first apparition.” Visualization of the spatial distribution of the selected stars is shown in Figure 1. The detailed analysis of the results of RRc and RRd stars has been demonstrated in Duan et al. (2021). In this paper, we present the measurements of RRab and Blazhko-type RR Lyrae variables and compare the properties between different types of RR Lyrae stars.
The emission and absorption components are fitted with the scale width versus shape method for the hydrogen lines (Sersic 1968; Clewley et al. 2002). We use two 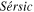 functions (Xue et al. 2008; Yang et al. 2014; Duan et al. 2020) as
functions (Xue et al. 2008; Yang et al. 2014; Duan et al. 2020) as

to fit the profile. Uncertainties are provided by error propagation with the covariance matrix and Monte Carlo method (Andrae 2010).
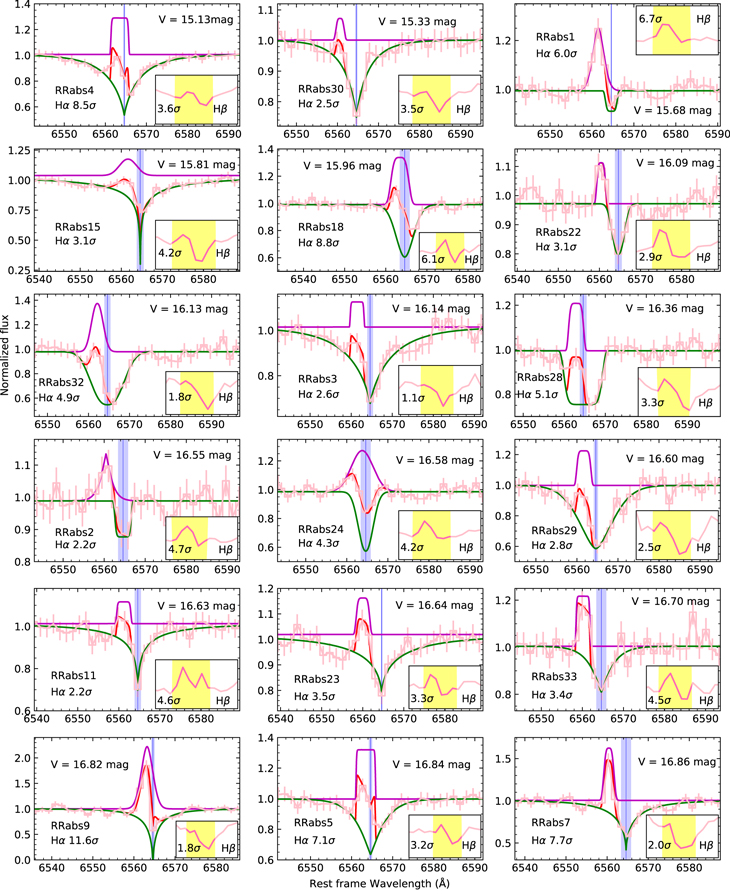
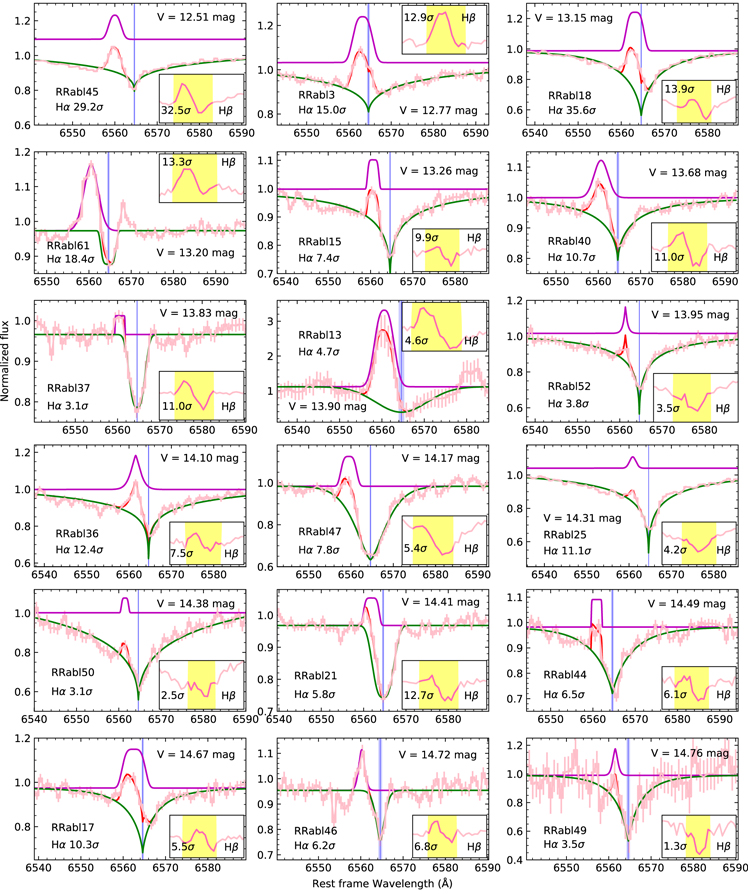
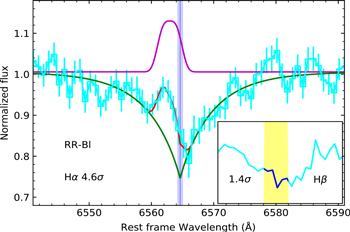
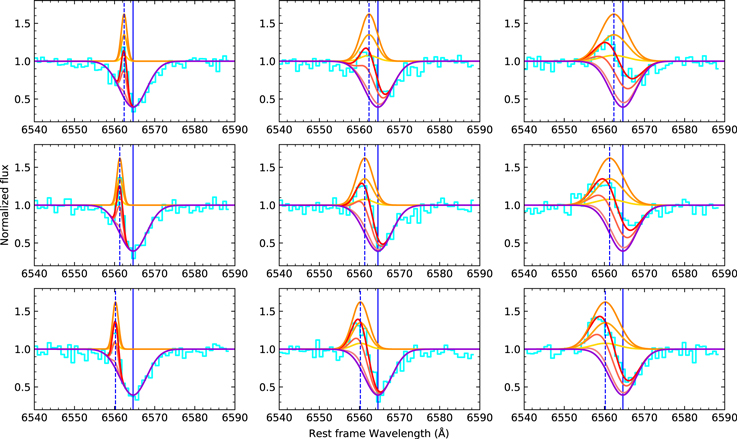
Figures 3 and 4 show the fitting examples of selected RRab stars in SDSS and LAMOST, respectively, which display the blueshifted emission in Hα. Figure 5 shows the fitting result of the Blazhko-type RR Lyrae star with the “first apparition” detected. The wavelength axis is in the stellar rest frame. Flux is normalized by continuum. The Hα emissions are shown as pink profiles. Hβ profiles are shown in the subplots. The significances of the blueshifted emissions for both Hα and Hβ are also shown. The candidates are adopted when the signal of Hα is over 2σ and the signal of Hβ is over 1σ.
Figure 3. Visualization of examples of fitting results of RRab that show hydrogen emission in SDSS. The wavelength axis is in the stellar rest frame. The fitted blueshifted Hα emission lines are shown as pink profiles. Green profiles denote fitted absorption lines. Red profiles represent the combination of fitted emission and absorption lines. Vertical blue lines denote the Hα line laboratory wavelength. The Hβ profiles are shown in the subplots. The significances of the emission lines denote the S/N. The examples are ordered by V.
Download figure:
Standard image High-resolution imageFigure 4. Same as Figure 3, but for selected RRab stars in LAMOST.
Download figure:
Standard image High-resolution imageFigure 5. Same as Figure 3, but for a selected Blazhko-type RR Lyrae star in LAMOST.
Download figure:
Standard image High-resolution imageThe radial velocity of the blueshifted hydrogen emission in the stellar rest frame is calculated as
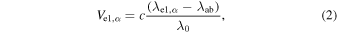
where λe1,α denotes the wavelength corresponding to the central wavelength of the emission line, λab denotes the central wavelength of the absorption line, and λ0 denotes the laboratory wavelength.
We provide measurements of redshift ze1,α and radial velocity in the stellar rest frame Ve1,α , normalized flux Fluxe1,α , and FWHM of the emission and absorption FWHMe1,α in the stellar rest frame of the blueshifted hydrogen emission. Parameters of the selected RR Lyrae variables and measurements of the “first apparitions” are summarized in Tables 1 and 2. RR Lyrae stars with SDSS spectra that exhibit the first apparition are marked as RRabs (s for SDSS) and those with LAMOST spectra and hydrogen emission as RRabl (l for LAMOST). The star “RR-Bl” denotes the Blazhko-type RR Lyrae star with LAMOST spectra and hydrogen emission (l for LAMOST). It was temporarily classified as a “Blazhko-type RR Lyrae variable” because it was not accurately classified owing to the significant modulation in the Catalina Sky Survey. In this work, RR-Bl is characterized as an RRab star using the pre-whitening sequence method in Section 5.
Table 1. Parameters of Selected RRab Stars from SDSS
| Object | R.A. (J2000) | Decl. (J2000) | Period | V | Amp | ze1,α | Ve1,α | Fluxe1,α | FWHMe1,α |
|---|---|---|---|---|---|---|---|---|---|
| (deg) | (deg) | (days) | (mag) | (mag) | (km s−1) | (Å) | |||
| RRabs1 | 6.20764 | +1.21571 | 0.68042 | 15.68 | 1.00 | − 4.72E − 4 ± 1.86E − 4 | −141 ± 79 | 0.25 | 3.05 |
| RRabs2 | 11.87371 | +13.91740 | 0.69140 | 16.55 | 0.83 | − 6.35E − 4 ± 1.87E − 4 | −190 ± 79 | 0.15 | 2.48 |
| RRabs3 | 19.11867 | −10.71342 | 0.48310 | 16.14 | 1.08 | − 4.84E − 4 ± 1.88E − 4 | −145 ± 80 | 0.11 | 3.32 |
| RRabs4 | 28.70903 | +0.25027 | 0.63698 | 15.13 | 1.14 | − 1.68E − 4 ± 1.87E − 4 | −50 ± 79 | 0.28 | 4.30 |
| RRabs5 | 32.71725 | +0.63203 | 0.51342 | 16.84 | 1.17 | − 1.77E − 4 ± 1.87E − 4 | −53 ± 79 | 0.32 | 4.69 |
| RRabs6 | 44.24281 | −1.15499 | 0.51943 | 17.79 | 0.97 | − 5.76E − 4 ± 1.88E − 4 | −173 ± 80 | 0.21* | 1.63 |
| RRabs7 | 122.43165 | +57.50441 | 0.52138 | 16.86 | 1.10 | − 6.37E − 4 ± 1.85E − 4 | −191 ± 79 | 0.62 | 2.52 |
| RRabs8 | 139.15997 | +30.14284 | 0.57204 | 17.13 | 0.89 | − 2.75E − 4 ± 1.88E − 4 | −82 ± 80 | 0.29 | 3.58 |
| RRabs9 | 144.23392 | +2.39681 | 0.68102 | 16.82 | 0.13 | − 2.16E − 4 ± 9.45E − 5 | −65 ± 34 | 1.22 | 3.27 |
| RRabs10 | 146.65068 | +15.99970 | 0.52099 | 17.73 | 0.85 | − 1.92E − 4 ± 1.86E − 4 | −57 ± 79 | 0.48 | 4.69 |
| RRabs11 | 149.11227 | +15.52289 | 0.65209 | 16.63 | 0.94 | − 5.20E − 4 ± 1.86E − 4 | −156 ± 79 | 0.10 | 3.44 |
| RRabs12 | 151.83224 | +53.47885 | 0.61787 | 17.10 | 0.61 | − 3.41E − 4 ± 1.15E − 4 | −102 ± 49 | 0.34 | 5.91 |
| RRabs13 | 152.83864 | +5.17696 | 0.64363 | 17.05 | 0.93 | − 2.46E − 4 ± 1.85E − 4 | −74 ± 79 | 0.24 | 4.70 |
| RRabs14 | 153.59429 | +40.33244 | 0.49947 | 17.16 | 0.98 | − 4.67E − 4 ± 1.88E − 4 | −140 ± 80 | 0.13 | 2.38 |
| RRabs15 | 167.19900 | −15.19530 | 0.57329 | 15.81 | 0.76 | −4.55E − 4±9.61E − 5 | −136 ± 49 | 0.14 | 4.84 |
| RRabs16 | 172.30798 | +28.80851 | 0.56680 | 17.72 | 0.71 | − 2.95E − 4 ± 1.85E − 4 | −89 ± 79 | 0.17 | 3.11 |
| RRabs17 | 186.58595 | −2.44612 | 0.62669 | 17.19 | 0.67 | − 2.68E − 4 ± 6.97E − 5 | −80 ± 60 | 0.49 | 4.51* |
| RRabs18 | 189.30895 | +14.44229 | 0.57156 | 15.96 | 0.89 | − 1.81E − 4 ± 1.86E − 4 | −54 ± 79 | 0.35 | 4.37 |
| RRabs19 | 197.03942 | +13.81974 | 0.51911 | 17.32 | 1.03 | − 2.64E − 4 ± 1.88E − 4 | −79 ± 80 | 0.45 | 3.39 |
| RRabs20 | 199.00117 | +11.91443 | 0.52698 | 17.54 | 1.07 | − 7.74E − 5 ± 6.52E − 5 | −23 ± 34 | 0.52 | 4.52 |
| RRabs21 | 202.86013 | +7.47637 | 0.54216 | 17.11 | 1.15 | − 4.81E − 4 ± 1.00E − 4 | −144 ± 42 | 0.18 | 2.78 |
| RRabs22 | 204.98954 | +58.16789 | 0.57165 | 16.09 | 0.93 | − 6.40E − 4 ± 1.88E − 4 | −192 ± 80 | 0.14 | 2.13 |
| RRabs23 | 220.46840 | +31.95186 | 0.57671 | 16.64 | 0.91 | − 6.96E − 4 ± 1.87E − 4 | −209 ± 79 | 0.14 | 3.24 |
| RRabs24 | 223.62869 | +40.07005 | 0.66732 | 16.58 | 0.63 | − 1.32E − 4 ± 1.87E − 4 | −40 ± 79 | 0.29 | 6.25* |
| RRabs25 | 238.83554 | +31.23341 | 0.56251 | 17.31 | 0.91 | − 2.78E − 4 ± 1.87E − 4 | −83 ± 79 | 0.31 | 3.27 |
| RRabs26 | 242.93547 | +10.72981 | 0.55029 | 17.31 | 1.02 | − 5.83E − 4 ± 1.14E − 4 | −175 ± 65 | 1.14* | 0.12 |
| RRabs271 | 247.42582 | +35.28750 | 0.63104 | 17.38 | 0.92 | − 3.45E − 4 ± 1.88E − 4 | −103 ± 80 | 0.25 | 4.42 |
| RRabs272 | 247.42582 | +35.28750 | 0.63104 | 17.38 | 0.92 | − 3.82E − 4 ± 1.54E − 4 | −115 ± 62 | 0.16 | 4.30 |
| RRabs28 | 248.63333 | +22.76128 | 0.55024 | 16.36 | 0.96 | − 2.63E − 4 ± 1.86E − 4 | −79 ± 79 | 0.21 | 3.63 |
| RRabs29 | 249.81254 | +32.90717 | 0.63611 | 16.60 | 0.91 | − 4.49E − 4 ± 1.88E − 4 | −135 ± 80 | 0.23 | 3.42 |
| RRabs30 | 259.17579 | +34.27990 | 0.57687 | 15.33 | 0.75 | − 6.08E − 4 ± 1.87E − 4 | −182 ± 79 | 0.07 | 2.01 |
| RRabs31 | 261.94862 | +65.60181 | 0.57442 | 17.32 | 0.55 | − 3.66E − 4 ± 2.27E − 5 | −110 ± 56 | 0.77 | 3.13 |
| RRabs32 | 331.06979 | +0.96542 | 0.50032 | 16.13 | 0.71 | − 3.76E − 4 ± 4.50E − 5 | −113 ± 37 | 0.39 | 3.26 |
| RRabs33 | 338.12842 | −8.48267 | 0.52279 | 16.70 | 1.09 | − 6.80E − 4 ± 1.87E − 4 | −204 ± 79 | 0.21 | 3.38 |
Note. (1): period, V, and Amp (amplitude) are produced by the Catalina Sky Survey. (2): ze1,α represents the redshift of the emission component of the “first apparition” in the stellar rest frame. (3): Ve1,α represents the radial velocity of the emission component of the “first apparition” in the stellar rest frame. (4): Fluxe1,α indicates the normalized flux of the emission. (5): FWHMe1,α indicates the FWHM of the emission. (6): the names like RRabs271 mean that there is not only one spectrum of one star. (7): the measurements with * denote low-quality results. (8): the stars are ordered by R.A.(J2000).
Download table as: ASCIITypeset image
Table 2. Parameters of Selected RRab and Blazhko-type Stars from LAMOST
| Object | R.A.(J2000) | Decl.(J2000) | Period | V | Amp | ze1,α | Ve1,α | Fluxe1,α | FWHMe1,α |
|---|---|---|---|---|---|---|---|---|---|
| (deg) | (deg) | (days) | (mag) | (mag) | (km s−1) | (Å) | |||
| RRabl1 | 26.68188 | +23.58775 | 0.65160 | 17.01 | 0.90 | − 5.04E − 4 ± 9.89E − 5 | −151 ± 42 | 0.14 | 1.62 |
| RRabl2 | 33.40705 | +30.47452 | 0.63676 | 15.73 | 0.57 | − 5.33E − 4 ± 3.86E − 5 | −160 ± 17 | 0.14 | 1.92 |
| RRabl3 | 34.39211 | +21.71650 | 0.56668 | 12.77 | 0.67 | − 2.11E − 4 ± 1.51E − 5 | −63 ± 16 | 0.21 | 4.84 |
| RRabl4 | 37.83211 | +23.74759 | 0.64989 | 16.90 | 0.39 | − 4.69E − 4 ± 9.87E − 5 | −141 ± 42 | 0.30 | 1.14 |
| RRabl51 | 42.25593 | +1.34632 | 0.57374 | 15.96 | 0.93 | − 6.09E − 4 ± 9.87E − 5 | −183 ± 42 | 0.07 | 3.08 |
| RRabl52 | 42.25593 | +1.34632 | 0.57374 | 15.96 | 0.93 | − 3.71E − 4 ± 4.08E − 5 | −111 ± 16 | 0.12 | 2.11 |
| RRabl6 | 42.86087 | +2.45366 | 0.61441 | 15.77 | 0.85 | − 7.48E − 4 ± 4.53E − 5 | −224 ± 16 | 0.12 | 2.91 |
| RRabl7 | 45.98163 | +16.53199 | 0.59756 | 17.02 | 0.80 | − 6.27E − 4 ± 9.93E − 5 | −188 ± 42 | 0.12* | 2.26 |
| RRabl8 | 47.38816 | +18.92607 | 0.47025 | 17.12 | 1.18 | − 4.77E − 4 ± 5.94E − 5 | −143 ± 20 | 0.19 | 2.07 |
| RRabl9 | 47.46535 | +5.02683 | 0.51977 | 17.69 | 0.94 | − 5.86E − 4 ± 4.94E − 5 | −176 ± 16 | 0.19 | 1.98 |
| RRabl10 | 47.61406 | +13.10191 | 0.52153 | 16.90 | 0.96 | − 5.63E − 4 ± 9.89E − 5 | −169 ± 42 | 0.14 | 0.86 |
| RRabl111 | 72.68140 | +3.79305 | 0.55219 | 16.11 | 0.77 | − 2.36E − 4 ± 2.62E − 5 | −71 ± 21 | 0.30 | 4.65 |
| RRabl112 | 72.68140 | +3.79305 | 0.55219 | 16.11 | 0.77 | − 2.77E − 4 ± 8.91E − 5 | −83 ± 40 | 0.44 | 3.76 |
| RRabl121 | 78.84653 | +8.10691 | 0.59066 | 16.62 | 0.63 | − 6.09E − 4 ± 4.73E − 5 | −183 ± 31 | 0.51 | 3.85 |
| RRabl122 | 78.84653 | +8.10691 | 0.59066 | 16.62 | 0.63 | − 6.15E − 4 ± 4.99E − 5 | −184 ± 33 | 0.45 | 3.63 |
| RRabl13 | 84.93823 | −3.42164 | 0.45415 | 13.90 | 1.07 | − 6.20E − 4 ± 2.21E − 5 | −186 ± 31 | 2.20 | 5.00 |
| RRabl14 | 113.32693 | +34.50516 | 0.53281 | 16.64 | 0.88 | − 4.31E − 4 ± 3.47E − 5 | −129 ± 31 | 0.25 | 2.38 |
| RRabl15 | 134.54286 | +15.80513 | 0.54316 | 13.26 | 0.76 | − 6.08E − 4 ± 9.87E − 5 | −182 ± 42 | 0.10 | 2.68 |
| RRabl161 | 144.36704 | +56.59926 | 0.52854 | 16.67 | 0.94 | − 5.50E − 4 ± 9.89E − 5 | −165 ± 42 | 0.22 | 2.45 |
| RRabl162 | 144.36704 | +56.59926 | 0.52854 | 16.67 | 0.94 | − 5.11E − 4 ± 9.89E − 5 | −153 ± 42 | 0.19 | 0.76 |
| RRabl163 | 144.36704 | +56.59926 | 0.52854 | 16.67 | 0.94 | − 4.62E − 4 ± 2.50E − 5 | −138 ± 18 | 0.28 | 0.26 |
| RRabl17 | 144.45373 | +0.16152 | 0.55127 | 14.67 | 0.99 | − 3.23E − 4 ± 3.80E − 5 | −97 ± 16 | 0.18 | 5.52 |
| RRabl18 | 145.76492 | +10.31705 | 0.67384 | 13.15 | 0.73 | − 2.21E − 4 ± 1.43E − 5 | −66 ± 8 | 0.25 | 4.20 |
| RRabl19 | 147.23862 | +17.52836 | 0.53657 | 15.85 | 1.06 | − 5.78E − 4 ± 9.89E − 5 | −173 ± 42 | 0.16 | 2.65 |
| RRabl20 | 148.41207 | +26.51218 | 0.57894 | 17.06 | 0.76 | − 2.85E − 4 ± 5.56E − 5 | −85 ± 34 | 0.30 | 5.33 |
| RRabl21 | 149.35586 | +3.66790 | 0.53401 | 14.41 | 1.04 | − 4.24E − 4 ± 2.76E − 5 | −127 ± 14 | 0.09 | 3.69 |
| RRabl22 | 156.00410 | +23.57355 | 0.57618 | 16.23 | 0.87 | − 6.83E − 4 ± 3.16E − 5 | −205 ± 32 | 0.21 | 3.74 |
| RRabl23 | 156.42426 | +27.70770 | 0.54505 | 17.72 | 1.01 | − 1.43E − 4 ± 3.55E − 5 | −43 ± 27 | 0.43 | 3.96 |
| RRabl24 | 158.23468 | +9.95462 | 0.57453 | 15.13 | 0.71 | − 5.07E − 4 ± 4.13E − 5 | −152 ± 26 | 0.13 | 2.83 |
| RRabl25 | 160.76055 | +6.57957 | 0.51591 | 14.31 | 0.78 | − 5.71E − 4 ± 3.26E − 5 | −171 ± 10 | 0.07 | 1.77 |
| RRabl26 | 163.78099 | −3.94871 | 0.83472 | 15.20 | 1.19 | − 2.70E − 4 ± 2.50E − 5 | −81 ± 11 | 0.13 | 5.09 |
| RRabl27 | 172.95127 | +16.94800 | 0.62769 | 15.56 | 0.87 | − 5.17E − 4 ± 9.93E − 5 | −155 ± 42 | 0.11 | 2.59* |
| RRabl28 | 186.22131 | +3.89524 | 0.50837 | 16.62 | 0.98 | − 6.40E − 4 ± 9.87E − 5 | −192 ± 42 | 0.12 | 1.87 |
| RRabl29 | 190.79904 | +44.92621 | 0.59282 | 15.56 | 0.96 | − 2.05E − 4 ± 5.82E − 5 | −61 ± 34 | 0.33 | 10.26 |
| RRabl30 | 196.40574 | +59.99944 | 0.51326 | 15.42 | 1.11 | − 4.77E − 4 ± 3.70E − 5 | −143 ± 14 | 0.11 | 3.35 |
| RRabl31 | 196.74774 | +16.74280 | 0.57767 | 17.35 | 0.55 | − 5.39E − 4 ± 5.04E − 5 | −162 ± 19 | 0.27 | 2.60 |
| RRabl32 | 201.57540 | +2.64155 | 0.65792 | 14.97 | 0.83 | − 3.48E − 4 ± 3.81E − 5 | −104 ± 29 | 0.23 | 3.57 |
| RRabl33 | 204.94889 | +15.59276 | 0.53250 | 15.04 | 1.09 | − 4.19E − 4 ± 4.14E − 5 | −126 ± 19 | 0.18 | 4.34 |
| RRabl34 | 207.17689 | +41.91878 | 0.54509 | 15.27 | 0.91 | − 5.64E − 4 ± 9.87E − 5 | −169 ± 42 | 0.16 | 2.28 |
| RRabl35 | 207.84723 | +3.96548 | 0.62922 | 15.22 | 1.06 | − 5.50E − 4 ± 8.25E − 5 | −165 ± 25 | 0.07 | 3.69 |
| RRabl36 | 208.18557 | −2.30798 | 0.57549 | 14.10 | 1.04 | − 4.63E − 4 ± 2.47E − 5 | −139 ± 10 | 0.18 | 2.44 |
| RRabl37 | 211.07900 | −4.10587 | 0.55437 | 13.83 | 0.90 | − 6.13E − 4 ± 9.89E − 5 | −184 ± 42 | 0.05 | 2.36 |
| RRabl38 | 219.15778 | +14.79704 | 0.52376 | 15.85 | 1.00 | − 6.19E − 4 ± 2.74E − 5 | −186 ± 10 | 0.18 | 1.02 |
| RRabl39 | 221.29128 | +1.50971 | 0.67651 | 14.97 | 0.89 | − 6.69E − 4 ± 9.93E − 5 | −200 ± 42 | 0.08 | 2.42 |
| RRabl40 | 221.37085 | −4.02095 | 0.51691 | 13.68 | 0.96 | − 6.04E − 4 ± 2.43E − 5 | −181 ± 11 | 0.12 | 3.90 |
| RRabl41 | 224.32736 | +22.98642 | 0.57342 | 15.42 | 0.92 | − 6.17E − 4 ± 9.91E − 5 | −185 ± 42 | 0.07 | 2.56 |
| RRabl42 | 233.40562 | +0.43740 | 0.51954 | 15.78 | 0.82 | − 4.45E − 4 ± 9.95E − 5 | −133 ± 42 | 0.11 | 2.86 |
| RRabl43 | 235.23457 | +10.96986 | 0.58815 | 15.29 | 0.79 | − 6.42E − 4 ± 4.46E − 5 | −192 ± 14 | 0.06 | 2.28 |
| RRabl44 | 239.16098 | +4.04318 | 0.55646 | 14.49 | 0.81 | − 5.68E − 4 ± 9.89E − 5 | −170 ± 42 | 0.11 | 2.52 |
| RRabl45 | 239.38257 | +28.63362 | 0.66540 | 12.51 | 0.53 | − 7.04E − 4 ± 1.54E − 5 | −211 ± 9 | 0.14 | 3.18 |
| RRabl46 | 240.30956 | +2.61588 | 0.66357 | 14.72 | 1.00 | − 6.70E − 4 ± 3.41E − 5 | −201 ± 22 | 0.16 | 1.61 |
| RRabl47 | 240.35335 | +27.02554 | 0.52700 | 14.17 | 0.84 | − 7.82E − 4 ± 2.51E − 5 | −235 ± 11 | 0.14 | 3.78 |
| RRabl48 | 242.48518 | +6.42657 | 0.64348 | 15.75 | 0.88 | − 1.74E − 4 ± 2.08E − 5 | −52 ± 15 | 0.25 | 4.26 |
| RRabl49 | 242.93347 | +17.00636 | 0.49055 | 14.76 | 1.04 | − 4.70E − 4 ± 7.38E − 5 | −141 ± 29 | 0.19 | 1.31 |
| RRabl50 | 245.90139 | +36.42249 | 0.57302 | 14.38 | 1.12 | − 4.80E − 4 ± 9.91E − 5 | −144 ± 42 | 0.08 | 1.70 |
| RRabl51 | 249.52973 | −3.43423 | 0.56249 | 14.86 | 1.00 | − 4.67E − 4 ± 9.91E − 5 | −140 ± 42 | 0.10 | 0.98 |
| RRabl52 | 250.09389 | +15.06886 | 0.69196 | 13.95 | 0.74 | − 5.01E − 4 ± 3.18E − 5 | −150 ± 10 | 0.15 | 0.75 |
| RRabl53 | 253.42009 | +34.38424 | 0.61463 | 15.56 | 0.53 | − 5.78E − 4 ± 9.93E − 5 | −173 ± 42 | 0.16 | 1.34 |
| RRabl54 | 254.49119 | +30.71234 | 0.54937 | 16.84 | 0.91 | − 1.69E − 4 ± 6.38E − 5 | −51 ± 33 | 0.43 | 3.93 |
| RRabl55 | 259.42280 | +41.32834 | 0.57087 | 14.77 | 0.86 | − 6.95E − 4 ± 1.82E − 5 | −208 ± 8 | 0.15 | 3.43 |
| RRabl56 | 261.66390 | +40.15591 | 0.63667 | 17.75 | 0.94 | − 1.03E − 4 ± 5.16E − 5 | −31 ± 31 | 0.41 | 7.09 |
| RRabl57 | 266.22514 | +42.81815 | 0.51673 | 15.43 | 1.02 | − 2.46E − 4 ± 3.86E − 5 | −74 ± 15 | 0.17 | 4.38 |
| RRabl58 | 319.48228 | −3.03425 | 0.61376 | 15.60 | 0.44 | − 9.01E − 4 ± 9.91E − 5 | −270 ± 42 | 0.13 | 0.91 |
| RRabl59 | 347.44815 | +29.67568 | 0.60791 | 16.68 | 0.63 | − 5.50E − 4 ± 9.89E − 5 | −165 ± 42 | 0.07 | 1.72 |
| RRabl60 | 352.58414 | +21.11239 | 0.52758 | 14.91 | 0.97 | − 5.88E − 4 ± 1.74E − 5 | −176 ± 7 | 0.17 | 2.44 |
| RRabl61 | 357.69274 | +33.35102 | 0.53392 | 13.20 | 0.77 | − 6.29E − 4 ± 2.33E − 5 | −189 ± 15 | 0.19 | 3.95 |
| Object | R.A.(J2000) | Decl.(J2000) | Periodf | G | AmpG | ze1,α | Ve1,α | Fluxe1,α | FWHMe1,α |
| (deg) | (deg) | (days) | (mag) | (mag) | (km s−1) | (Å) | |||
| RRabl62 | 10.49515 | +33.83455 | 0.50996 | 16.89 | 0.91 | − 6.51E − 4 ± 1.49E − 5 | −195 ± 10 | 0.31 | 2.72 |
| RRabl631 | 178.36094 | +53.77534 | 0.54987 | 17.38 | 0.81 | − 5.60E − 4 ± 2.04E − 5 | −168 ± 11 | 0.38 | 2.03 |
| RRabl632 | 178.36094 | +53.77534 | 0.54987 | 17.38 | 0.81 | − 5.72E − 4 ± 9.89E − 5 | −171 ± 42 | 0.26 | 2.49 |
| RRabl64 | 180.93050 | +5.48829 | 0.57846 | 15.58 | 1.05 | − 3.50E − 4 ± 3.28E − 5 | −105 ± 15 | 0.19 | 2.51 |
| RRabl65 | 196.90430 | +73.59784 | 0.51574 | 15.04 | 0.97 | − 4.89E − 4 ± 2.84E − 5 | −147 ± 12 | 0.14 | 2.89 |
| RRabl66 | 248.94414 | −4.75558 | 0.66401 | 16.06 | 0.67 | −1.35E − 4±9.81E − 5 | −41 ± 42 | 0.59 | 3.47* |
| RRabl67 | 285.76599 | +57.32673 | 0.52887 | 14.43 | 0.88 | − 2.74E − 4 ± 2.58E − 5 | −82 ± 13 | 0.11 | 5.66 |
| RRabl68 | 291.08516 | +34.27314 | 0.56338 | 15.12 | 0.72 | − 5.80E − 4 ± 5.86E − 5 | −174 ± 18 | 0.06 | 2.12 |
| RRabl69 | 324.40104 | +44.46210 | 0.47481 | 16.30 | 0.87 | − 5.72E − 4 ± 9.91E − 5 | −171 ± 42 | 0.14 | 1.48 |
| RRabl701 | 326.54851 | +26.93884 | 0.57201 | 13.73 | 0.89 | − 6.67E − 4 ± 2.53E − 5 | −200 ± 10 | 0.14 | 3.17 |
| RRabl702 | 326.54851 | +26.93884 | 0.57201 | 13.73 | 0.89 | − 2.49E − 4 ± 1.43E − 5 | −75 ± 9 | 0.17 | 4.63 |
| Object | R.A.(J2000) | Decl.(J2000) | Period | V | Amp | ze1,α | Ve1,α | Fluxe1,α | FWHMe1,α |
| (deg) | (deg) | (days) | (mag) | (mag) | (km s−1) | (Å) | |||
| RR-Bl | 322.09646 | +20.22167 | 0.54283 | 14.84 | 0.41 | − 2.55E − 4 ± 9.83E − 5 | −76 ± 42 | 0.12 | 3.98 |
Notes. (1): period, V, and Amp (amplitude) are produced by the Catalina Sky Survey. Periodf, G, and AmpG are produced by the Gaia mission. Periodf denotes the fundamental period in the Gaia catalog. (2): ze1,α represents the redshift of the emission component of the “first apparition” in the stellar rest frame. (3): Ve1,α represents the radial velocity of the emission component of the “first apparition” in the stellar rest frame. (4): Fluxe1,α indicates the normalized flux of the emission. (5): FWHMe1,α indicates the FWHM of the emission. (6): the names like RRabl51 mean that there is not only one spectrum of one star. (7): the measurements with * denote low-quality results. (8): the stars are ordered by R.A. (J2000).
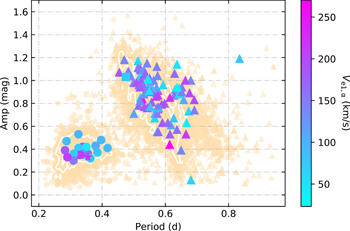
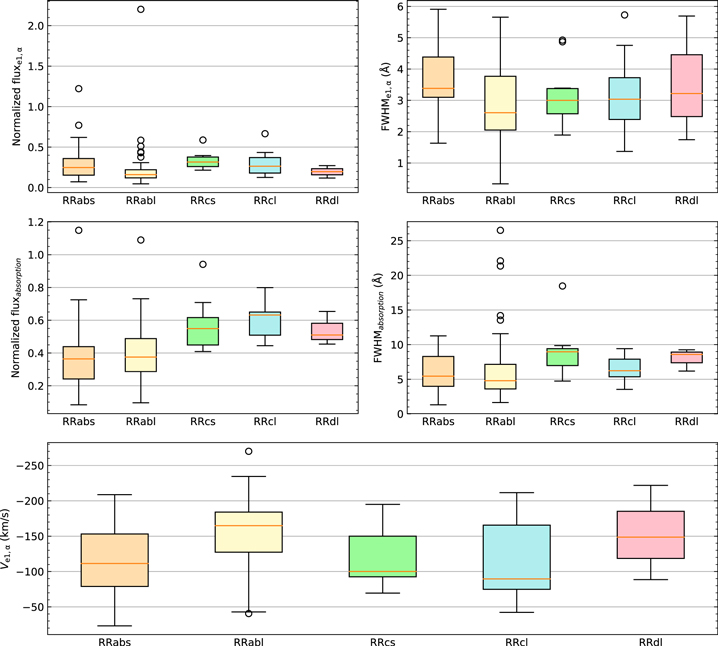
The distribution of selected stars on the period–amplitude diagram is shown in Figure 6. A clear gap divides RRab and RRc stars into two groups. RRab stars have longer periods and larger mean amplitudes than RRc stars. Box plots of the measurements are displayed in Figure 7. The mean value of normalized flux and the FWHM of emission or absorption of RRc stars are higher than those of RRab stars. The mean value of Ve1,α of RRab stars is higher than that of RRc stars.
Figure 6. Period–amplitude diagram. Selected stars with period and amplitude produced by the Catalina Sky Survey are shown. Corresponding relation: triangle—RRab; circle—RRc; star—RRd; square—the Blazhko-type RR Lyrae variable. The variation of color shows different absolute values of Ve1,α . Light-yellow points in the background denote the whole sample of RR Lyrae stars. 1σ regions are shown as white contours.
Download figure:
Standard image High-resolution imageFigure 7. Box plots of measurements of different types of stars that show the “first apparitions.” Top left: normalized flux of emission (Fluxe1,α ); top right: FWHM of emission (FWHMe1,α ); middle left: normalized flux of absorption; middle right: FWHM of absorption; bottom: Ve1,α of different types of stars that show the “first apparition.”
Download figure:
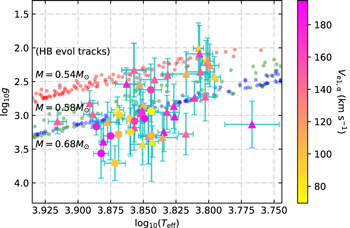
Standard image High-resolution imageFigure 8 shows the log Teff–log g diagram. We adopt measurements of Teff and log g generated by SSPP if available. Despite that the pipeline is not optimized for RR Lyrae stars and these values are derived from co-added spectra, the parameters from the pipeline can provide an overall description of log g–log Teff distribution of various subgroups. Overall, RRc stars are hotter and have larger log g than RRab stars. We also display simulated HB evolutionary tracks for stars in the background, which was calculated with expansion and semiconvection of the core and enhanced oxygen composition from Dorman (1992), to show regions of different masses. The line consisting of red, green, and blue points in the background indicates evolutionary tracks for stars with M = 0.54, 0.58, and 0.68 M⊙, respectively.
Figure 8. log Teff–log g diagram for RR Lyrae stars that show the “first apparition.” Measurements of Teff and log g were produced by SSPP, if available. Points with error bars denote the selected stars with the “first apparitions.” Triangles denote RRab stars, while circles denote RRc stars. The variations of color show different Ve1,α . The line consisting of red, green, and blue points in the background indicates the simulated HB evolutionary tracks for stars with M = 0.54, 0.58, and 0.68 M⊙, respectively (Dorman 1992).
Download figure:
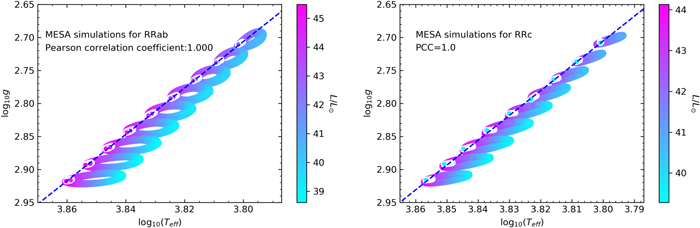
Standard image High-resolution imageThe presence of the “first apparition” indicates a certain range of phase, just before the maximum luminosity. Figure 9 shows that points during a certain phase interval from RR Lyrae variables with similar properties are concentrating on a linear path on the log Teff–log g diagram when the effective temperature changes, which is demonstrated by a series of simulations using Modules for Experiments in Stellar Astrophysics (MESA; Paxton et al. 2019). We simulated nine RRab and nine RRc stars with various initial effective temperatures in identical duration of evolution, while other initial parameters remain the same. The initial parameters are Minit = 0.55 M⊙, Linit = 41.687 L⊙, Xinit = 0.736, and Zinit = 0.008, which indicates [Fe/H] = −0.33 (Das et al. 2018). Teff ranges from 6300 to 7100 K in step width of 100 K. In Figure 9, variation of color indicates the changing of luminosity, which can stand for the changing phase. Points at around ϕ = 0.91 are located on a linear path, highly characterized by Pearson correlation coefficients (PCCs) of 1.000 and 0.999 for RRab and RRc, respectively. The observation points on the log Teff–log g diagram have a diffuse distribution because our selected stars have various physical properties such as mass, luminosity, and metallicity. The different parameters make them deviate from one linear path.
Figure 9. log Teff–log g diagram generated from MESA simulations for RRab and RRc stars. Left: evolutionary tracks for a series of RRab stars during identical time intervals. The variations of color denote different L/L⊙. The white points indicate the locations of ϕ = 0.91. The black dashed line shows the linear fitting for the white points. For initial parameters, Minit = 0.55 M⊙, Linit = 41.687 L⊙, Xinit = 0.736, and Zinit = 0.008, which indicates [Fe/H] = −0.33. Initial Teff ranges from 6300 to 7100 K in step width of 100 K. Right: evolutionary tracks for a series of RRc stars during identical time intervals. Other comments are the same as for panel (a).
Download figure:
Standard image High-resolution image5. Analysis of Frequency Components in the RR-Bl
We analyze the r-band light curve of RR-Bl with a time span of 974.66 days with a standard successive pre-whitening method (Moskalik & Kołaczkowski 2009). Observations in poor quality (catflags ≠ 0) have been removed. We fit the data using a nonlinear least-squares procedure with the sine series of the following form at each step:

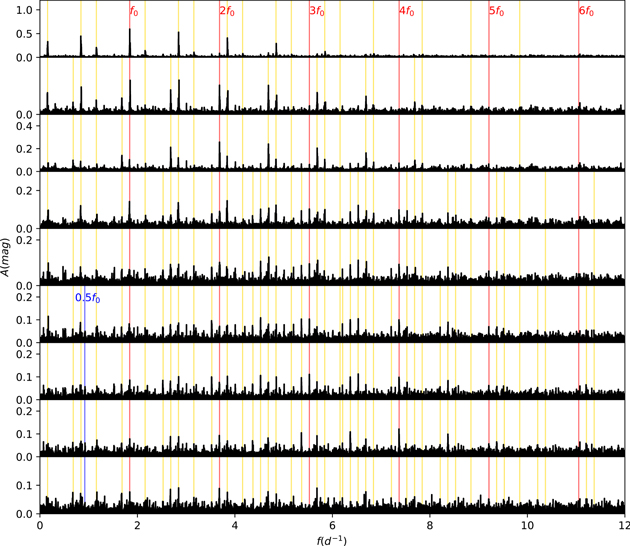
where fk denotes independent frequencies detected in discrete Fourier transform of the data and their possible linear combinations. The pre-whitening sequence for RR-Bl is shown in Figure 10. We find a full light curve solution for RR-Bl and produce the fitting results of the light curve in Figure 11.
Figure 10. Pre-whitening sequence for RR-Bl. The uppermost panel displays the power spectrum of the original data. The lower eight panels show power spectra after removing consecutive frequencies. nf0 lines are marked with red color. 0.5f0 is marked with blue color. Yellow lines are linear combinations expressed by nf0 + λc fc , while fc is the daily cadence.
Download figure:
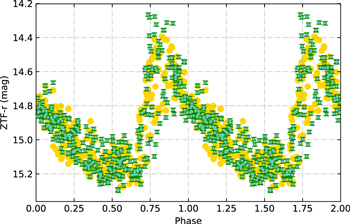
Standard image High-resolution imageFigure 11. Regeneration of a light curve of RR-Bl with full light-curve solution. Green points with error bars are photometric observations from ZTF-r. Golden points are regenerated points with full light-curve solution.
Download figure:
Standard image High-resolution imageAccording to f0 = 1.84226, we derive the fundamental period P0 = 0.54281 days and A0 = 0.242 mag. Apart from f0 and its linear combinations nf0, we detect significant signals that can be expressed as nf0 + λc fc , where fc ≈ 1, which can be explained as daily cadence. According to the pre-whitening sequence for RR-Bl, only one independent dominant frequency is detected. So RR-Bl is an RRab star with a strong Blazhko effect.
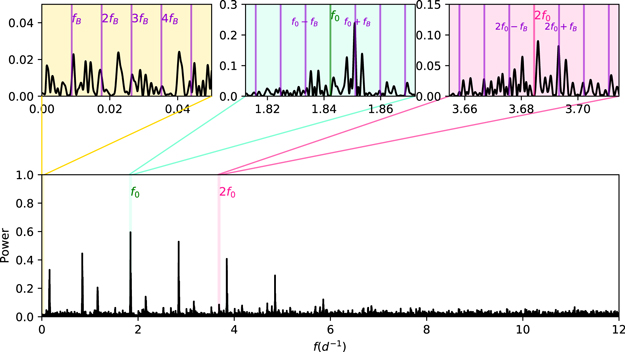
The additional close side peaks at the fundamental frequency denote long-term modulation (Smolec et al. 2015). In Figure 12, the amplifying pattern is shown. The weak signatures beside nf0 indicate a possible Blazhko-type modulation, with fB ≈ 0.009 and PB ≈ 111.111 days. The signals other than f0 + fB are not significant enough compared to others. Larger data sets are needed for a more precise analysis.
Figure 12. Pre-whitened power spectrum of RR-Bl. The bottom panel displays the power spectrum of the original data. The top panels display power spectra after pre-whitening, showing the fine structures in low frequency (left), around f0 (middle), and around 2f0 (right).
Download figure:
Standard image High-resolution image6. Detection Rate and Mock Data Test
The observational detection rate of blueshifted emission features in hydrogen lines of RR Lyrae stars is defined as

where Nobs represents the number of RRab stars with featured emission components in LAMOST survey spectra. Nsat denotes the input number of RRab variables in the survey plan that are observed and with the S/Ns of spectra greater than 15. Such a definition of detection rate has an implicit assumption, that all RRab stars possess shock-triggered emission and may or may not be detected in random sampling spectroscopic observations, depending on the observational timing and the strength of the emission feature.
The results of η are as follows: 1.84%—RRab in SDSS; 1.06%—RRc in SDSS; 2.87%—RRab in LAMOST; 1.45%—RRc in LAMOST; 2.97%—RRd; and 2.56% for Blazhko-type RR Lyrae stars in LAMOST. The detection rate of the “first apparition” of RRc stars is significantly lower than that of RRab stars. We suggest that the detection rate in LAMOST is higher than that in SDSS because the sources in SDSS are fainter and the pixel resolution of LAMOST is higher than that of SDSS. For SDSS, we choose the “spCFrame spectra,” and the pixel resolutions are about 4150 at Hα and 4180 at Hβ. For LAMOST, the pixel resolutions are about 7800 at Hα and 8400 at Hβ. The pixel resolution influences our results because one selecting criterion is that both emission and absorption components should contain at least two observational points. We set up two simulations for RRab variables in LAMOST: one on mock spectra to test the performance of our pipeline, the other on the observational strategy to investigate the occurrence of the “first apparition.”
First, we test the performance of our pipeline on mock spectra generated based on the distributions of real observational parameters. We propose that the recognition rate of the shock wave signatures can be described as

where A = “the first apparition is observed on the spectra” and B = “the signal meets the criterion.” We recognize P(A) as the real detection rate, while P(AB) is the detection rate from the search. P(AB) is lower than P(A) owing to finite S/N and our strict criterion of selecting the stars with the “first apparition,” which is described in Section 3.
We generate the mock spectra that have the “first apparition” and apply our 1D pattern recognition pipeline on the mock sample to estimate P(B∣A). The parameterizations of the simulated “first apparitions” are shown in Figure 13. The mock spectrum is regenerated as two Gaussian-like profiles between 6540 and 6590 Å. The central line of the absorption component is fixed at the rest wavelength of Hα. The blueshift of the emission, the ratio between the flux of the emission and absorption component, and the ratio between the FWHM of the emission and absorption component determine the shape of the simulated spectrum. The parameters of the Gaussian profiles are set as random values under Gaussian distribution based on the fitted distributions of the parameters of the selected RRab stars in LAMOST. Random noises are added up to the profiles to reproduce real situations, under Gaussian distribution, where σ is the error of normalized flux. The resolutions and S/Ns of mock spectra are taken from real observations.
Figure 13. Simulated template of spectra of the “first apparitions.” The wavelength axis is in the stellar rest frame. The blueshifted Hα emission lines are shown as orange profiles. The Hα absorption lines are shown as blue profiles. Red profiles show the shapes of the “first apparitions.” Cyan profiles display the profile with random noises. Vertical blue solid lines denote the Hα line laboratory wavelength. Vertical blue dashed lines denote the central wavelength of the emissions.
Download figure:
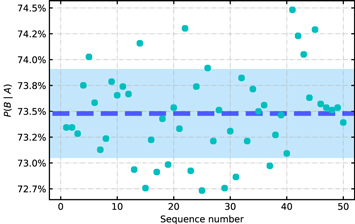
Standard image High-resolution imageWe apply our pipeline on the mock sample and set up this simulation for 50 times. We only adopt the result of RRab stars in LAMOST, because the pixel resolution of SDSS is low and the search in SDSS relies more on eye-checking. Moreover, the size of the sample of RRc, RRd, and Blazhko-type RR Lyrae stars is not large enough to provide reliable parameter distribution. Figure 14 displays the result that P(B∣A) = 73.48% ± 0.43%. This means that, for a spectrum exhibiting blueshifted hydrogen emission with random flux, FWHM, and blueshift, there should be a 73.48% ± 0.43% chance that our algorithm would recognize.
Figure 14. P(B∣A) of RRab stars in LAMOST.
Download figure:
Standard image High-resolution imageSecond, we set up a following simulation on the real observational strategy to investigate the occurrence of “first apparition.” The simulation is based on the real parameters, including detection mode, exposure time, observation interval, observing frequency, and the period of the corresponding RR Lyrae star for each spectrum satisfying S/N > 15.
In the simulation we preset that every star in the testing sample would have a “first apparition.” The exposure time for a spectrum with S/N > 15 is then used as an observing window. Exposure times and observation intervals are obtained from real spectra. In the simulation, we set that the “first apparition” shows up for a short period of time before maximum luminosity in each pulsation cycle. Chadid (2011) reported that the “first apparition” appears over ∼5% of the whole pulsation cycle. Gillet et al. (2019) reported that the “first apparition” presents during ϕ = 0.892–0.929 in RR Lyr, accounting for about 3.7% of the whole period. Their researches are based on bright RR Lyrae stars. Our sample is much larger and contains a lot of faint stars. In the simulation, we assume that the “first apparition” accounts for about 4% of the whole period.
As a matter of fact, too long-time exposures can smooth out the emission features in the hydrogen lines. Therefore, we assume that the survival time of the emission feature and the exposure time should overlap with at least 70% of the exposure time for a clear signal. Each case in which the emission overlaps with more than 70% of the exposure time yields one valid catch for a star. The number of valid catches of one star changes with observation time. The possibility of detecting a star with the “first apparition” is P(B∣A), [1 − (1 − P(B∣A))2], or [1 − (1 − P(B∣A))3] during the time when the star has one, two, or three valid catches, respectively.
For the result, the number of detected RRab stars with blueshifted hydrogen emission in LAMOST from the simulation is about 371.79, while our observational result is 70. The result of the simulation is larger than our observational result. In our simulation we assume that every star in our sample exhibits the “first apparition.” However, not every RRab star has a visible “first apparition” in the real survey owing to variant shock strength. The occurrence of “first apparition” can be estimated as
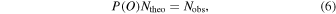
where O = “the star shows the first apparition.” We define P(O) as the occurrence of “first apparition.” Ntheo is the number of detected RRab stars with blueshifted hydrogen emission in LAMOST from simulation. Nobs denotes the number of detected RRab stars with blueshifted hydrogen emission in LAMOST in our survey. Here Ntheo = 371.79, Nobs = 70, and P(O) ≈ 18.83%.
We suggest that P(O) is underestimated. First, our simulation does not contain the selecting of Hβ emissions owing to the low resolution of the spectra, so P(B∣A) is overestimated. Another reason for the overestimation of P(B∣A) is that we used the observed distribution but not the intrinsic distribution for emission flux. Moreover, in the progress of fitting we abandon some spectra that may show shock signatures but are hard to identify or provide no valid measurements, or contain no valid Hβ emissions. That is to say, more than 18.83% of the RRab stars show relatively strong “first apparition.”
7. Conclusions
In this work, we develop a handcrafted 1D pattern recognition searching algorithm and apply it to a large data set of single-epoch spectra of RR Lyrae stars, in order to fetch out the “first apparitions.” Through this survey, we found 33 RRab stars and 10 RRc stars in SDSS and 70 RRab stars, 10 RRc stars, 3 RRd stars, and 1 Blazhko-type RR Lyrae star in LAMOST. Based on the searching results, we set up the first population study of the RR Lyrae variables showing hypersonic shock waves.
We build up the largest database of blueshifted hydrogen emission in RR Lyrae stars. The features of the “first apparitions” are fitted by two Sérsic profiles. We provide measurements of redshift ze1,α and radial velocity in the stellar rest frame Ve1,α , normalized flux Fluxe1,α , and FWHM of the emission and absorption FWHMe1,α in the stellar rest frame of the blueshifted hydrogen emission. The distributions of measurements for different types are compared. We provide detailed analysis for the light curve of the Blazhko-type RR Lyrae star with ZTF DR5. We characterize this Blazhko-type RR Lyrae star as an RRab star with strong Blazhko modulations with a possible Blazhko period PB ≈ 111.111 days.
Finally, we set up two simulations for RRab variables in LAMOST. For the first one, we apply our algorithm on mock spectra to test the performance of our pipeline and to check the influence of the selecting criteria. The other simulation is based on the real observational strategy to investigate the occurrence of the blueshifted hydrogen emission in RRab variables in LAMOST. The result suggests that more than 18.83% of the RRab stars exhibit relatively strong “first apparition.” The nature of RR Lyrae variables will be more and more clear with the enormous volume of upcoming observational data.
The suggestions and comments by the anonymous referee are gratefully acknowledged. We thank the help from Dr. Hao-Tong Zhang, Dr. Zhong-Rui Bai, and Dr. Jian-Jun Chen for getting the single-epoch spectra from LAMOST. We acknowledge discussion with Dr. Anupam Bhardwaj. X.-W. D. acknowledges research support from the Cultivation Project for LAMOST Scientific Payoff and Research Achievement of CAMS-CAS and the Peking University President Scholarship. L.-C.D. acknowledges research support from the National Science Foundation of China through grants 11633005. X.-D.C. also acknowledges support from the National Natural Science Foundation of China through grant 11903045. H.-W.Z. acknowledges research support from the National Natural Science Foundation of China (NSFC) under No. 11973001 and National Key R&D Program of China No. 2019YFA0405504. We thank Mark Taylor for the TOPCAT software. The CSS survey is funded by the National Aeronautics and Space Administration under grant No. NNG05GF22G issued through the Science Mission Directorate Near-Earth Objects Observations Program. The CRTS survey is supported by the U.S. National Science Foundation under grants AST-0909182 and AST-1313422. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. The Gaia archive website is https://archives.esac.esa.int/gaia. This publication makes use of data products from the Wide-field Infrared Survey Explorer, which is funded by the National Aeronautics and Space Administration. The All-Sky Automated Survey for Supernovae (ASAS-SN) group is partially funded by Gordon and Betty Moore Foundation 5 yr grant GBMF5490. They are also supported by NSF Grants AST-151592 and AST-1908570. ATLAS construction and operations are funded by grants 80NSSC18K0284 and 80NSSC18K1575 under the NASA Planetary Defense Office and Near-Earth Objects Observations program (NEOO). This work also made use of data from the Zwicky Transient Facility project (ZTF), based on observations obtained with the Samuel Oschin 48-inch Telescope at the Palomar Observatory as part of the Zwicky Transient Facility project. ZTF is supported by the National Science Foundation under grant No. AST-1440341. Funding for SDSS-III has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, and the U.S. Department of Energy Office of Science. The SDSS-III website is http://www.sdss3.org/. Participating Institutions of the SDSS-III Collaboration include the University of Arizona, the Brazilian Participation Group, Brookhaven National Laboratory, Carnegie Mellon University, University of Florida, the French Participation Group, the German Participation Group, Harvard University, the Instituto de Astrofisica de Canarias, the Michigan State/Notre Dame/JINA Participation Group, Johns Hopkins University, Lawrence Berkeley National Laboratory, Max Planck Institute for Astrophysics, Max Planck Institute for Extraterrestrial Physics, New Mexico State University, New York University, Ohio State University, Pennsylvania State University, University of Portsmouth, Princeton University, the Spanish Participation Group, University of Tokyo, University of Utah, Vanderbilt University, University of Virginia, University of Washington, and Yale University. The Guoshoujing Telescope (the Large Sky Area Multi-Object Fiber Spectroscopic Telescope LAMOST) is a National Major Scientific Project built by the Chinese Academy of Sciences. Funding for the project has been provided by the National Development and Reform Commission. LAMOST is operated and managed by the National Astronomical Observatories, Chinese Academy of Sciences.
Software: NumPy (Harris et al. 2020), SciPy (Virtanen et al. 2020), AstroPy (Astropy Collaboration et al. 2018), Matplotlib (Hunter 2007), Scikit-learn (Pedregosa et al. 2011), PyAstronomy (Czesla et al. 2019), TOPCAT (Taylor 2005).
Footnotes
- 7
Some of the RR Lyrae stars with strong Blazhko modulation in the Catalina Sky Survey cannot be accurately classified owing to the significant modulation. They are temporarily classified as “Blazhko-type RR Lyrae variables.” But they are not all of the stars that show the Blazhko effect.