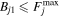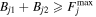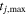Abstract
Gravitationally lensed Type Ia supernovae (SNe Ia) may be the next frontier in cosmic probes, able to deliver independent constraints on dark energy, spatial curvature, and the Hubble constant. Measurements of time delays between the multiple images become more incisive due to the standardized candle nature of the source, monitoring for months rather than years, and partial immunity to microlensing. While currently extremely rare, hundreds of such systems should be detected by upcoming time domain surveys. Others will have the images spatially unresolved, with the observed lightcurve a superposition of time-delayed image fluxes. We investigate whether unresolved images can be recognized as lensed sources given only lightcurve information, and whether time delays can be extracted robustly. We develop a method that we show can identify these systems for the case of lensed SNe Ia with two images and time delays exceeding ten days. When tested on such an ensemble, without microlensing, the method achieves a false-positive rate of ≲5%, and measures the time delays with a completeness of ≳93% and with a bias of ≲0.5% for Δtfit ≳ 10 days. Since the method does not assume a template of any particular type of SN, the method has the (untested) potential to work on other types of lensed SNe systems and possibly on other transients as well.
1. Introduction
Gravitational lensing is the most visually striking demonstration of the curvature of spacetime. An individual source emits signals that reach the observer from different directions and at different times, forming multiple images. Moreover, these image separations and time delays carry important cosmological information on the distances and gravitational potentials along the lines of sight. For a variable source, repeated monitoring of the image flux allows estimation of the time delay, an important ingredient for the time delay distance mapping the cosmic expansion.
Time delay distances derived from monitoring quasars over years or even a decade are in use as a cosmological probe (Treu & Marshall 2016; Wong et al. 2019; Millon et al. 2020; Shajib et al. 2020). Quasars are plentiful, but their intrinsic time variability is unpredictable and it is challenging to separate out microlensing—additional time variation due to motion of objects near the lines of sight. This often means that several years (≳5) of data must be accumulated before time delays can be measured with precision. With forthcoming surveys, detections of lensed Type Ia supernovae (SNe Ia)—supernovae were the source Refsdal (1964) originally proposed for the time delay cosmography technique—will become much more numerous. To date, only two systems have currently been published, namely those of Kelly et al. (2015) and Goobar et al. (2017). These have the advantage of possessing better known time behavior (i.e., their flux versus time, or lightcurves, are more standard), with a characteristic timescale of a couple of months, enabling more rapid time delay estimation, and they have a period of insensitivity to microlensing when measured in multiple wavelength filters (Goldstein et al. 2018).
Supernova time delays have been put forward as ways to measure the Hubble constant (Oguri & Marshall 2010), with application to the first lensed SN, called Refsdal, discussed in detail in Kelly et al. (2015, 2016), Rodney et al. (2016), Grillo et al. (2018), and Vega-Ferrero et al. (2018). This involves cluster lensing with clearly spatially separated images. Simulation studies of lensed SN with image brightenings well-separated in time, i.e., time delays of ≳60 days, are discussed in Pierel & Rodney (2019). Here, we concentrate on the opposite regime, where images are neither spatially nor temporally separated—unresolved. The fraction and numbers of resolved versus unresolved systems depends sensitively on survey characteristics including instrument response, survey strategy, signal-to-noise cuts, etc. Useful estimations based on published characteristics plus some further assumptions for the Nancy Grace Roman Space Telescope and Rubin Observatory are presented in Pierel et al. (2021).
Since typical galaxy lensing time delays are less than or on the order of the SN rise and fall time, when the images are not spatially well-separated, the observation is of an overlapping, summed lightcurve, offering a challenge to the time delay measurement. Indeed, one expects many lensed SNe to be unresolved rather than resolved. Here, we take up the challenge and explore whether we can (1) recognize an SN lightcurve as being composed of multiple unresolved images and (2) accurately measure the time delay. Due to their property of having somewhat standard lightcurve shapes, and given that upcoming surveys will devote considerable resources to studying them, including through follow-up observations, we focus on SNe Ia. This focus also follows from the use of SN Ia as luminosity distance indicators in addition; the combination of luminosity distance and time delay distance (possibly from two different SN Ia samples) can be quite powerful for a variety of cosmological characteristics; see, e.g., Denissenya et al. (2018), Liao et al. (2017, 2019, 2020), Lyu et al. (2020), Pandey et al. (2020), Wong et al. (2019), Arendse et al. (2020), Taubenberger et al. (2019), Collett et al. (2019), and Treu & Marshall (2016). However, since our fitting approach is quite flexible and does not assume a fixed template of any particular type of SN, the method may be suitable for extracting time delays (and relative magnifications) from lensed systems of other types of SN as well as from a wide variety of other transients in extension. For simplicity, we focus only on two-image lensed SN Ia systems in this work.
In Section 2, we discuss the data sets expected from upcoming surveys, including the multiband lightcurve and noise properties. We introduce our lightcurve fitting method in Section 3, and we test it in several ways on mock data characteristic of upcoming surveys in Section 4. A summary and avenues for future development are presented in Section 5.
2. Forthcoming Supernova Data Sets
High-redshift supernovae are efficiently discovered with cadenced “rolling” wide-field imaging surveys (Astier et al. 2006). Fields of view of tens of arcminutes and greater ensure that multiple SNe are active within an untargeted pointing. A cadence of several days ensures that those supernovae will be discovered, ideally early in their evolution, to ensure follow-up observations. The survey telescope, instrumentation, and design define the search volume, both in terms of the monitored solid angle and the depth, which then determine the number of supernovae that can be discovered.
Gravitationally lensed SNe are relatively rare; only one in roughly a thousand SNe are expected to be strongly lensed. Only surveys that monitor a large volume over a long control time are capable of discovering interesting numbers of lensed SNe. The Zwicky Transient Facility (ZTF; Bellm et al. 2018) and the Vera C. Rubin Observatory Legacy Survey of Space and Time (LSST; Ivezić et al. 2019) are two surveys that will discover an interesting number of gravitationally lensed SNe of all types.
ZTF is a three-year survey and is composed of a public survey, which monitors 15,000 deg2 every three nights to g, r ≈ 20.5 mag, a partnership survey that adds supplemental high-cadence g, r, and i exposures for a subset of sky, as well as Caltech time. The nominal LSST wide-fast-deep 10 yr survey (known as minion 1016) covers ∼20,000 deg2 and cycles ugrizy every two-to-three weeks to a limiting magnitude of ∼23.5 mag. Goldstein et al. (2019) forecast that ZTF (LSST) can make early discoveries of 0.02 (0.79) 91bg-like, 0.17 (5.92) 91T-like, 1.22 (47.84) Type Ia, 2.76 (88.51) Type IIP, 0.31 (12.78) Type IIL, and 0.36 (15.43) Type Ib/c lensed SNe per year. They also forecast that the surveys can discover at least 3.75 (209.32) Type IIn lensed SNe per year, for a total of at least 8.60 (380.60) lensed supernovae per year under fiducial observing strategies. The simulations and resultant lightcurves used to make these forecasts serve as the test data used in this article. We concentrate on the ZTF simulations in this work, to get an indication of nearer-term results. However, this method applies equally well to LSST simulation data; see also Wojtak et al. (2019), Huber et al. (2019), Verma et al. (2019), and Goldstein et al. (2018).
For lens systems with small Einstein radii, image separations of multiple images can be too small to be spatially resolved in observations. Goldstein et al. (2019) find that over half of strongly lensed SNe discovered by LSST will have a minimum angular separation of <1″ and a significant fraction of those will have separations of <05. Many strongly lensed supernova discoveries will thus be unresolved by traditional ground-based observations. Robust determination of time delays from the single observed lightcurve comprised of the sum of light from multiple unresolved images could be valuable in increasing the number of lensed supernova systems usable for cosmology from upcoming surveys.
Supplemental high-resolution imaging, e.g., from adaptive optics or space observations, can deliver important information. For example, an external determination of the number of images in the lensed system, and hence the number of time delays, fixes what otherwise would be a free parameter in the fit of an unresolved lightcurve. However, this would likely be at a single epoch, and the monitoring telescope that delivers the lightcurve might not separate the images. Thus, the technique presented here is still of use in these cases.
3. Fitting an Unresolved Lightcurve
3.1. Modeling the Lightcurve
The observed unresolved lightcurve is the sum of the fluxes from each of the unresolved images, each image i having the same lightcurve shape because it comes from the same source, but with differing amplitudes ai and delayed observed phases, i.e., dates of explosion ti .
The lightcurve observed in the jth filter (we use filter and band interchangeably), summed over NI images, can be written as
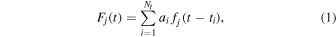
where fj is the intrinsic lightcurve in the jth filter. As the science measurements of interest are the relative time delays and magnifications, we work in terms of the parameters Δti ≡ ti − t1 and μi ≡ ai /a1 defined relative to the first, earliest image. For simplicity, one can choose t1 = 0 so that Equation (1) is
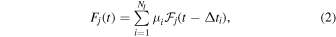
where of course μ1 = 1 and Δt1 = 0, and 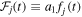 is a scaled version of the source lightcurve.
is a scaled version of the source lightcurve.
Our model fits both the underlying multiband lightcurve shapes,  , and the relative magnifications and time delays of each of the images. Using a fixed template for
, and the relative magnifications and time delays of each of the images. Using a fixed template for 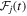 is unlikely to give the flexibility for fits to a diverse set of supernovae, and indeed may lead to biases on time delay estimation, so we want to keep
is unlikely to give the flexibility for fits to a diverse set of supernovae, and indeed may lead to biases on time delay estimation, so we want to keep 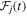 adaptable. The underlying multiband lightcurve shapes
adaptable. The underlying multiband lightcurve shapes 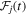 are modeled as a fiducial function with a shape that is generically similar to supernovae, modified multiplicatively by a truncated series of orthogonal functions. Specifically, we choose
are modeled as a fiducial function with a shape that is generically similar to supernovae, modified multiplicatively by a truncated series of orthogonal functions. Specifically, we choose  to be the product of a lognormal function multiplied by a basis expansion with respect to the first four Chebyshev functions,
to be the product of a lognormal function multiplied by a basis expansion with respect to the first four Chebyshev functions,
Chebyshev functions have been widely used in Crossing statistics to give the desired flexibility (Shafieloo et al. 2011; Shafieloo 2012a, 2012b; Hazra & Shafieloo 2014). The time variable in the crossing terms uses  .
6
.
6
In this model, the underlying lightcurve in a single filter is described by one normalization Nj and six shape parameters: bj , σj , C1,j , C2,j , C3,j , C4,j . Thus, to describe lightcurves composed of NI images in NB bands, there are 2(NI − 1) + 7NB + 1 parameters, where there is one parameter for the numerical fit shift parameter t1.
In this article, we make two simplifying restrictions. We concentrate on systems with only two images (or simply one if it is unlensed, for testing). The unresolved lightcurve consisting of two images is given by
where the lightcurve of the first image 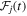 is described by Equation (3) (together with the shift parameter t1) and the second image by a shifted, scaled version of it. For the ZTF-like systems, we have observations in g, r, i filters. Therefore, we have 2 + 7 × 3 + 1 = 24 fit parameters, two of which are the parameters of cosmological interest, namely the relative time delay Δt between the images and their relative magnification μ. The second simplification is that here we do not include the effect of microlensing on the lightcurve (nor do the simulations we use from Goldstein et al. (2019)). Microlensing can introduce generally small, slowly changing magnifications that are different for each image, though correlated for the different filters of the same image. (Indeed, Goldstein et al. (2019) have shown that the color, i.e., differences between filters, is insensitive to microlensing for much of the phase relevant to time delay estimation.) For the small image separations we consider here for unresolved lensed SN, microlensing effects between images may also be reduced. Nevertheless, expanding our model to include further multiplicity of images and microlensing is planned for future work.
is described by Equation (3) (together with the shift parameter t1) and the second image by a shifted, scaled version of it. For the ZTF-like systems, we have observations in g, r, i filters. Therefore, we have 2 + 7 × 3 + 1 = 24 fit parameters, two of which are the parameters of cosmological interest, namely the relative time delay Δt between the images and their relative magnification μ. The second simplification is that here we do not include the effect of microlensing on the lightcurve (nor do the simulations we use from Goldstein et al. (2019)). Microlensing can introduce generally small, slowly changing magnifications that are different for each image, though correlated for the different filters of the same image. (Indeed, Goldstein et al. (2019) have shown that the color, i.e., differences between filters, is insensitive to microlensing for much of the phase relevant to time delay estimation.) For the small image separations we consider here for unresolved lensed SN, microlensing effects between images may also be reduced. Nevertheless, expanding our model to include further multiplicity of images and microlensing is planned for future work.
3.2. Sampling and Setting the Priors
We employ Hamiltonian Monte Carlo (HMC) for sampling, since it is well-suited to dealing with a few dozen parameters. Specifically, we use the PyStan package (Stan Development Team 2017), a Python interface to STAN (Carpenter et al. 2017). We set priors on the parameters as described below, balancing broadness of the priors with convergence efficiency. As priors tend to involve the astrophysics of the source, their specific values need to be adjusted depending on the type of transient. Here, we focus on normal SNe Ia. Apart from the specific priors, however, the method described in the main text should be broadly applicable to many unresolved lensed transients.
3.2.1. Prior on Time Delay and Magnification
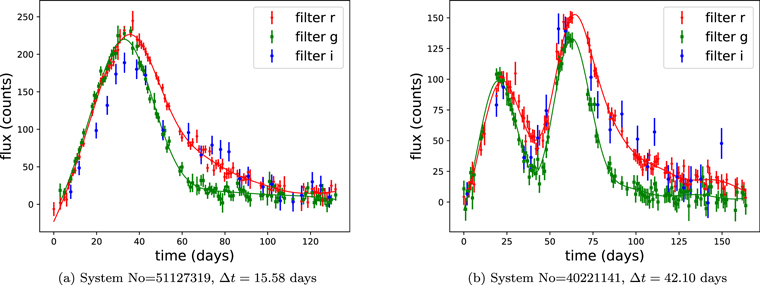
For time delays that are shorter than the characteristic source lightcurve width, the observed lightcurve of the combined images will tend to have one consolidated peak, while for longer time delays, two separate peaks—one for each of the images—may be evident (depending on the magnification ratio). Long time delays and large magnification ratios would tend to give larger angular separation also, leading to resolved rather than unresolved lensed supernovae. However, we will apply our method to a wide range of time delays, though we concentrate on the more difficult, lower end of the range, Δt ≲ 30. Examples of mock observed lightcurves of lensed supernovae are given in Figure 1.
Figure 1. Mock observations with ZTF characteristics are shown from the compilation of simulated SNe 1a (Goldstein et al. 2019) in g, r, i filters. Solid curves show a smoothing of the data, helpful for identifying the number of peaks by eye. Left panel has a smaller time delay and shows a single peak. Right panel has a longer time delay and shows two peaks corresponding to the two images. We do not use i-band data for determining the number of peaks, due to the generally poorer data quality and longer decline time.
Download figure:
Standard image High-resolution imageAs seen in Figure 1, when the peaks are well-separated, one can roughly estimate the time delay from the peak positions and the relative magnification from the ratio of the peaks. These estimations can be used to set tighter priors for these large time delay systems. Conversely, when there is no evident double-peak structure (in the filters we use), this imposes an upper limit on the time delay, based on the width of the peak. These features can be helpful in setting the priors on Δt (and μ in some cases) so that the fit converges faster and we ameliorate issues of nonconvergence, or degenerate or catastrophically false fits.
The procedure begins by identifying the peaks in the smoothed lightcurve data (this is solely for identifying the number of peaks; we use the full data in the fit). After testing different smoothing methods, we use the iterative smoothing algorithm with exponential kernel in Shafieloo et al. (2006) (see also Shafieloo 2007, 2012a; Shafieloo & Clarkson 2010; Aghamousa & Shafieloo 2015), with a smoothing scale of 12 days. While searching for peaks, to eliminate false peaks due to noise, we set a minimum height of the peaks relative to the tallest peak, minimum width, and minimum separation between peaks (details below).
- 1.If one peak is identified, the time delay is not very high and we set a prior 0 ≤ Δt ≤ 30. We use a wide prior range on the relative magnification: 0 ≤ μ ≤ 4. However, if the peak width is found to be very large, i.e., more than 20 days width at 80% of peak height, we adjust the prior ranges on the time delay and relative magnification—see Appendix A for details.
- 2.If two peaks are identified, the time delay is high and we can crudely estimate it as roughly the difference in the peak positions in time, say δ t. We also have an estimation for the relative magnification, roughly the ratio of the two peak heights, say r. We then use the following priors: (δ t − 15) ≤ Δt ≤ (δ t + 15) and r/2 ≤ μ ≤ 1.5r.
- 3.If more than two peaks are identified, we consider the two most prominent peaks and follow the treatment above. Future work will deal with systems that handle more than two images.
We follow the above steps for the g, r filters separately. If one filter has one peak while the other has two or more, we follow the two-peak procedure if the separation between the identified peaks of the two-peak filter is less than 30 days, otherwise we follow the one-peak procedure. (The logic here is that, for long true time delays, we would see two peaks in both filters; this step removes the spurious fitting of a noise fluctuation far on the tail of the lightcurve as a second peak.) We tested this algorithm extensively as described in Section 4.
3.2.2. Priors On Hyperparameters
The priors on the hyperparameters are given in Table 1. The fit generally prefers the hyperparameters to be somewhere in the middle of the prior ranges, e.g., mj ∼ 3.5 and σj ∼ 0.6. See Appendix A for further details, as well as Section 4.6 for when some of the nonphysical hyperparameter priors may be informative. In practice, we treat the normalization more subtly than the hyperparameter Nj , breaking out a scaling based on the maximum flux observed and then a zeroth-order basis function C0,j ; see Appendix B for details and Table 1 for the prior on C0,j .
Table 1. Priors On the Fit Hyperparameters
| Hyperparameter | Prior |
|---|---|
| σj | [0.4, 0.8] |
| bj | [3.0, 4.1] |
| C0,j | [0.4, 2] |
| Ck,j | [ − 5, 5] |
| t1 | [−5, 5] |
Note. Here, Ck,j is for k = 1, 2, 3, 4.
Download table as: ASCIITypeset image
In the fits, we use STAN (Carpenter et al. 2017; Stan Development Team 2017) to run HMC with seven chains, each with 6000 iterations and 1000 warm-up steps. We check the convergence of the chains by ensuring that the Gelman & Rubin (1992) convergence diagnostic parameter 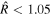 , as suggested by the STAN development team (Carpenter et al. 2017).
, as suggested by the STAN development team (Carpenter et al. 2017).
4. Results from Testing and Validation
Using simulated data, we apply the method proposed in Section 3 in four ways to test the results obtained for time delays.
- 1.Systematic approach: We analyze systems scanning through various values for the time delays, relative image magnifications, and noise levels, and find in what portion of this parameter space the method succeeds. These lightcurves are generated using the Hsiao template (Hsiao et al. 2007) with no microlensing, and observing conditions matched to those of Goldstein et al. (2019). We refer to this simulation tool based on the SNCosmo python package (Barbary 2014) as “LCSimulator” throughout this article.
- 2.Blind test: One author used LCsimulator to generate a set of unresolved lensed SN lightcurves with a variety of data properties, including several unlensed systems, and provided only the final summed lightcurve data to another author to be fit. This enables robust testing, as well as assessing false positives.
- 3.Applied test: More sophisticated lensed SN lightcurve simulations from Goldstein et al. (2019) (“the Goldstein set”) with less tightly controlled noise properties are used to assess the fitting method.
- 4.Validation: Once the method is finalized, we return to untested systems from the Goldstein simulated data set with even less tightly controlled noise properties and fit the unresolved lensed lightcurves.
4.1. Systematic Studies
In this section, we study a number of two-image systems simulated with properties scanning through time delay, relative magnification, and noise. We consider time delays Δt = 0, 2, 4, 6, …., 28, 30; i.e., a total of 16 time delays. For each time delay, we simulate three systems having μ = 0.5, 1, 2. Therefore, we have 16 × 3 = 48 systems in a set. We then simulate four such sets with different noise levels: 0.5%, 2.5%, 5%, and 10% of the maximum flux. The main goal of this exercise is to test how our method performs in different conditions, finding the range of validity in terms of the time delay, magnification, and noise level (or alternately, “testing to destruction”). Set 1 has an extremely small noise level, which is quite unrealistic, and serves to establish fundamental limits in the method. Set 4 has an extremely large noise level, where we expect large uncertainty in our estimations. Note that each set has 48 systems, out of which three are truly unlensed with Δt = 0 (and several others have time delays less than some surveys’ cadence).
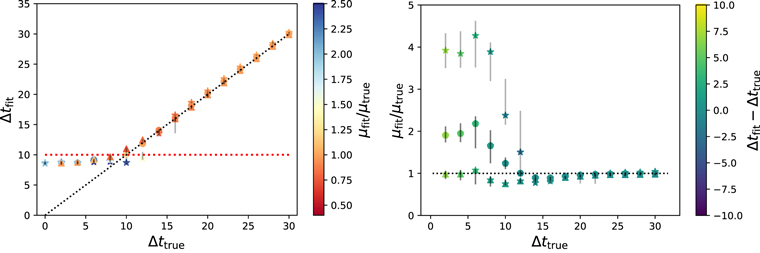
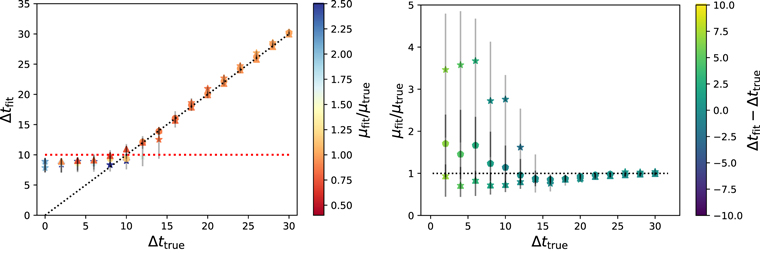
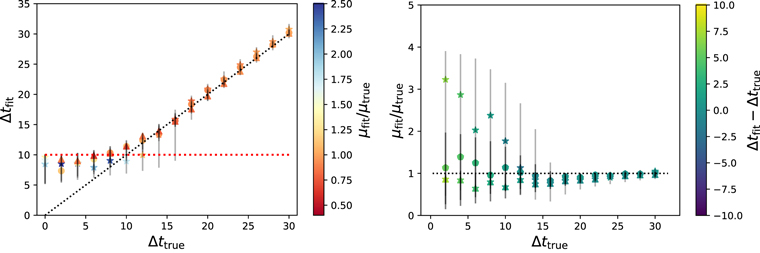
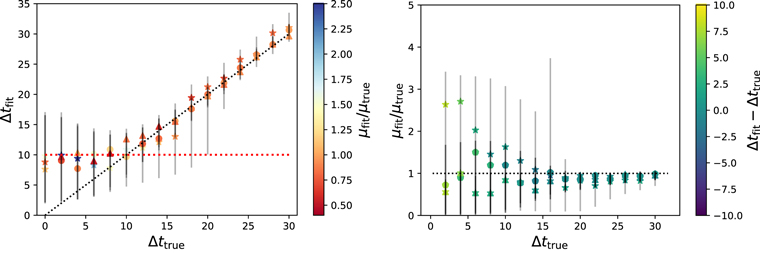
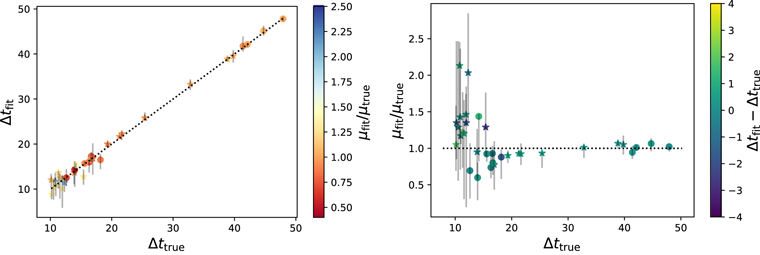
The summary of the results are shown in Figures 2–5 for the four sets (each with a different noise level). Each plot has 48 systems. The three markers, “star,” “filled circle,” and “triangle,” represent μtrue = 0.5, 1, and 2, respectively. The error bars shown here (and throughout this paper) are discussed in Section 4.6. The color bars represent the quantities (μfit/μtrue) in the left panels and Δtfit − Δttrue in the right panels. Note that, for unlensed systems, we have both Δttrue = 0 and μtrue = 0. Therefore, we arbitrarily set the color according to μfit for such systems and mark them using stars in the left panels; all systems with μfit/μtrue > 2.5 (basically bad fits for μ) have been marked with the dark blue color for μfit/μtrue = 2.5. The black dotted diagonals in the left panels of the figures represent Δtfit = Δttrue while the horizontal red dotted line is Δtfit = 10 days, below which the solutions depart from this relation. We quantify this further in Section 4.6.
Figure 2. Noise level = 0.5% (Set 1): We show Δtfit (left panel) and μfit/μtrue (right panel) vs. Δttrue. We obtain faithful results for fits giving time delays more than Δtfit = 10 days (dashed red horizontal line in the left panel). Stars, circles, and triangles represent μtrue = 0.5, 1, and 2, respectively, while color represents μfit/μtrue (left panel) and Δtfit − Δttrue (right panel). Error bars are 95% quantile around the median.
Download figure:
Standard image High-resolution imageFigure 3. Same as Figure 2, but for noise level = 2.5% (Set 2).
Download figure:
Standard image High-resolution imageFigure 4. Same as Figure 2, but for noise level = 5% (Set 3).
Download figure:
Standard image High-resolution imageFigure 5. Same as Figure 2, but for noise level = 10% (Set 4).
Download figure:
Standard image High-resolution imageFrom these plots, we observe the following:
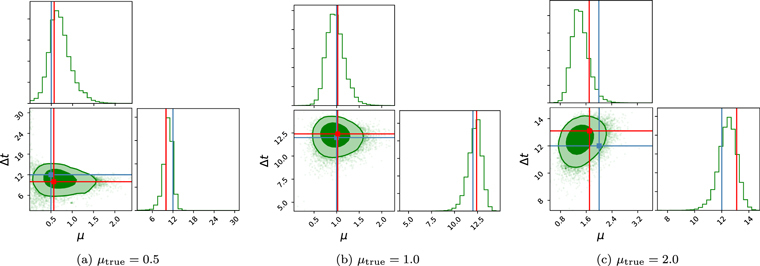
- 1.For all four sets, we recover the true solutions well when Δttrue > 10 days. While the cosmology focus is on Δtfit, we can also find μfit reasonably well. This is fairly robust with noise level, although the 10% level is noticeably more uncertain. Figure 6 shows an example of the 2D joint posterior and 1D probability distribution functions (PDFs) for Δt and μ.
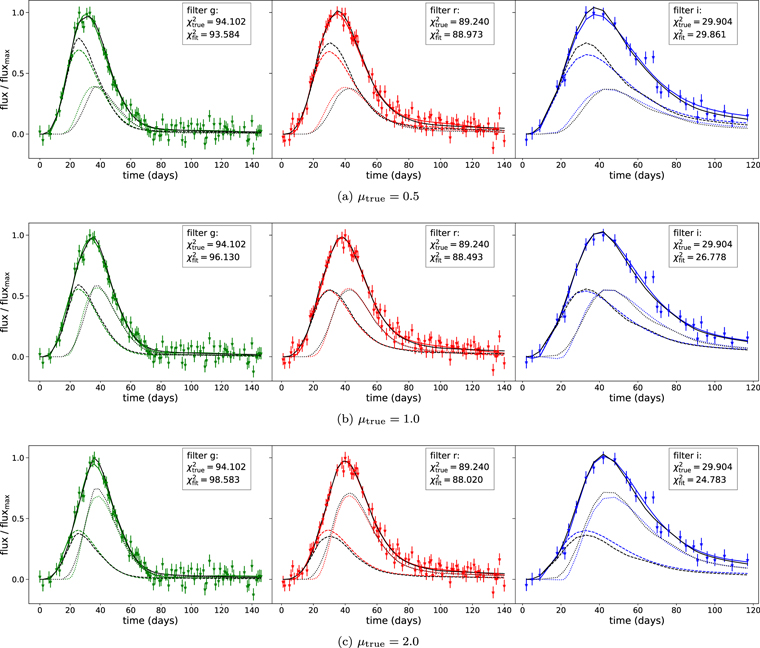
- 2.Furthermore, although again it is not the focus for cosmology, the individual image lightcurves match well with the true ones. Figure 7 presents an example of the image lightcurves, as well as the unresolved total lightcurve, compared to the inputs and data.
- 3.For Δttrue < 10 days, in all four sets, Δtfit does not trace Δttrue. Instead of following the true time delay, the estimated time delay remains stable around Δtfit ≲ 10 days for Δttrue < 10 days. This holds as well for a completely different intrinsic lightcurve approach not discussed in this paper, and seems likely to be due to the data sampling cadence.
Figure 6. Corner plot showing the 2D joint probability distribution and 1D PDFs for Δt and μ, marginalizing over all other parameters. This example is for noise level = 5.0% (Set 3), with Δttrue = 12 days, and three different relative magnifications: μtrue = 0.5, 1.0, 2.0. Blue crosshairs and points show the simulation input values, while red ones show our best-fit values.
Download figure:
Standard image High-resolution imageFigure 7. Simulated data with error bars (noise level = 5.0%, Set 3) for a system with Δttrue = 12 days. Columns show g, r, i bands. Rows show three different relative magnifications for the images: μtrue = 0.5, 1.0, 2.0 (top, middle, bottom panels, respectively). Black curves are the true lightcurves: dashed, dotted, and solid black curves represent the true lightcurves of the first image, second image, and their combination, respectively. Colored curves are our equivalent reconstructions in each filter using the best-fit parameters. While the key science quantity is merely the time delay, we do fit well the entire lightcurve, even for this moderately low time delay Δttrue = 12 days, for all the three magnifications. This is quantified through the χ2 values listed for the true and the reconstructed curves.
Download figure:
Standard image High-resolution imageThe bottom line is that, for unresolved lensed SN with Δttrue ≥ 10 days, our method can (1) identify them as lensed, (2) fit the time delay used for cosmology, and (3) further fit the magnification and individual lightcurve shapes (although these are not essential for cosmology). When the fit points to Δtfit < 10 days, we do not have confidence from this approach that the SN is actually lensed nor what its exact time delay is.
4.2. Systematic Studies for Unlensed Systems
In the systematic study presented in the previous section, we studied a total of 12 unlensed systems (having Δttrue = 0 and/or μtrue = 0), three cases in each of the four sets. In all the 12 unlensed cases, our fit estimates Δtfit < 10 days, and hence we would not claim detection of a lensed SN.
To investigate further, we study next a large number of unlensed systems, again simulated using LCsimulator. We consider 360 unlensed SN, 120 in each of three sets, with noise levels at 2.5%, 5%, 10% (of the maximum of the lightcurve). If we use our acceptance criterion Δtfit > 10 days suggested by Figures 3–5, then we have no false positives for the 2.5% noise level and about 8% false positives for the 5% and 10% noise levels. However, raising the acceptance to Δtfit > 12 days completely eliminates false positives: none out of the 360 would be mistakenly interpreted as unresolved lensed SN.
4.3. Blind Testing
To test the robustness of the developed analysis pipeline, one author simulated a set of unresolved SN lightcurves based on the Hsiao template (Hsiao et al. 2007), with no microlensing, and with observing conditions matched to those of Goldstein et al. (2019). This set included a range of time delays, as well as unlensed cases. Another author received only the final summed lightcurve data to carry out a fit, without further communication. This enabled testing without any case-by-case tweaking using knowledge that would be not be available for real data; in addition, it served as a further test of false positives.
This test used 100 systems with the noise level randomly set between 2.5% and 10% (of the maxima of the observed lightcurve). After the analysis was complete and fits were frozen, it was revealed that nine systems were unlensed and the remainder had time delays distributed over 6–30 days. Results are shown in Figure 8 and appear well in line with previous tests—good tracing of the true time delay and no false negatives.
Figure 8. Blind test: Same as Figure 2, but for a blind set having 100 systems, nine of which are unlensed while the time delays of the rest are distributed over 6–30 days. Stars and circles represent systems with μtrue ≤ 1 and μtrue > 1, respectively.
Download figure:
Standard image High-resolution image4.4. Applied Tests on the Goldstein Set
For more sophisticated lensed SN simulations, we employ the ZTF-Ia lensed SN simulations compiled in Goldstein et al. (2019) that fulfill the following criteria: (1) lightcurve visually appears smooth (and the shape is “like a lightcurve”); (2) the system has a minimum of 200 data points when combining g, r, i bands (typically the i-band data points are much fewer than for the g, r bands) and 0.5 ≤ μ ≡ μ2/μ1 ≤ 2, Δttrue ≥ 10 days. This gives rise to an initial set of 33 systems, with an average noise level of ∼7%.
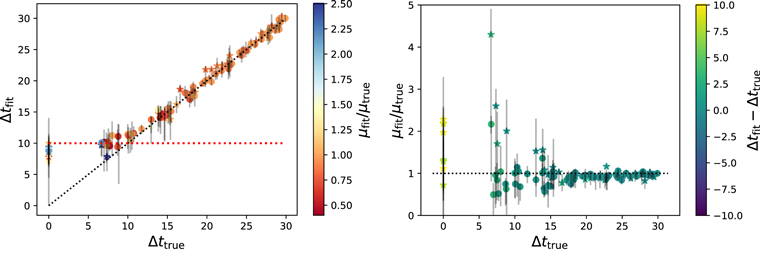
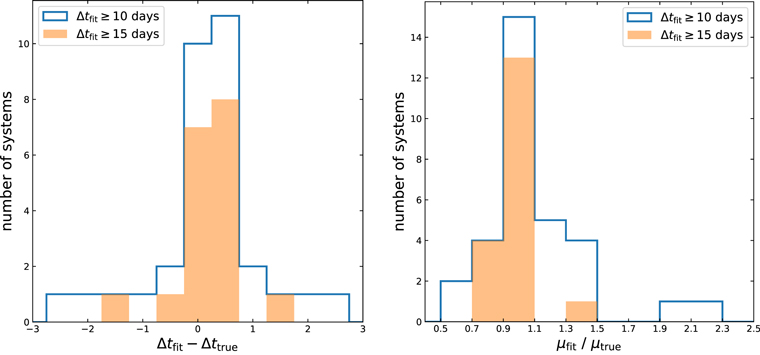
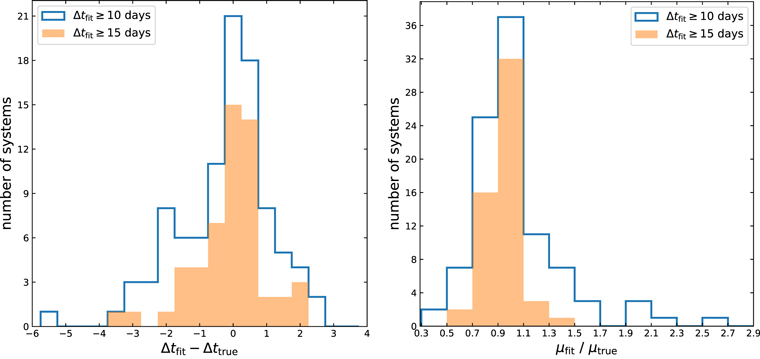
Our results for the time delays and magnifications appear in Figure 9. Again, the fits trace the true values. Note that 7 of the 33 systems are at higher time delays than we have previously considered and the fit continues to work well (this is unsurprising because the time delays are higher, but still useful to check). Figure 10 compiles the statistics of the fits by presenting the histograms of scatter of the best fit from the true values, for the outcomes where we accept the fit results—either Δtfit > 10 or 15 days. The histograms are highly peaked near the true values: only 2 of 33 cases are off by more than 2 days in the time delay, and none by more than 3 days.
Figure 9. Best-fit time delays for 33 ZTF-like systems from Goldstein et al. (2019) are shown with respect to the true values. Color bars show μfit/μtrue and Δtfit − Δttrue in the left and the right panel, respectively. Stars and filled circles represent systems with μtrue ≤ 1 and μtrue > 1, respectively. As this illustration shows, we get excellent fits and smaller error bars for systems with higher time delays.
Download figure:
Standard image High-resolution imageFigure 10. Histograms of the best-fit values of time delay and magnification from the set of 33 ZTF-like systems are shown relative to the true values, in bins of width 0.5 days in Δt and 0.2 in μ. Blue histogram in either panel consists of systems we could fit with confidence, i.e., for which Δtfit ≥ 10 (32 systems), with orange shaded regions restricted to those systems with Δtfit ≥ 15 days (18 systems). Note only 2 out of the 33 systems in this set have ∣Δtfit − Δttrue∣ > 2 days and none have ∣Δtfit − Δttrue∣ > 3. For most systems, the fits are quite close to the true value.
Download figure:
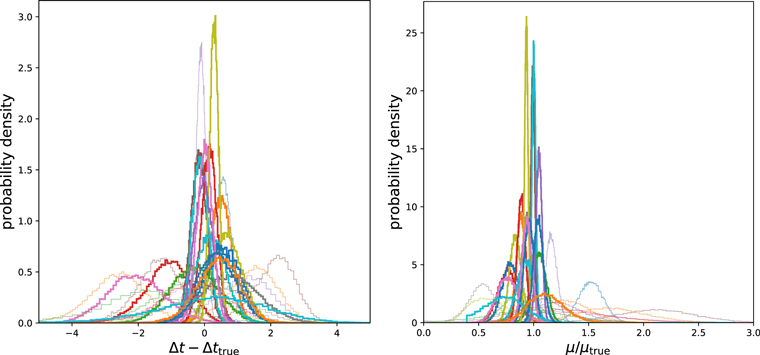
Standard image High-resolution imageSince more information is present in the full fit distributions, not just the best-fit values, Figure 11 presents the full 1D PDFs for the time delays and magnifications. They appear fairly Gaussian and the ensemble is well-peaked near the true values.
Figure 11. Rather than merely the best-fit values, here we show the full 1D probability densities (PDF) of time delay and magnification (relative to the true values) of the 33 systems, plotted simultaneously. Again, the full 1D histograms trace the true values quite well. Bolder curves denote systems with Δtfit > 15 days.
Download figure:
Standard image High-resolution image4.5. Validation Tests on the Goldstein Set
Finally, following the previous full program of testing, we apply the method to a larger sample from Goldstein et al. (2019). We consider systems with relaxed constraints on the relative magnification, 1/3 ≤ μtrue ≤ 3, while keeping the time delay range the same as the training set, 10 ≤ Δttrue ≤ 50 days. The other criteria pertaining to the data quality are kept the same except that, for the purpose of validation, we extend the testing by including noisier systems. The set of 71 systems so identified has a larger overall noise level (∼10.4%), compared to the previous samples; considering this together with the relaxed constraints, we therefore expect larger uncertainties and scatter.
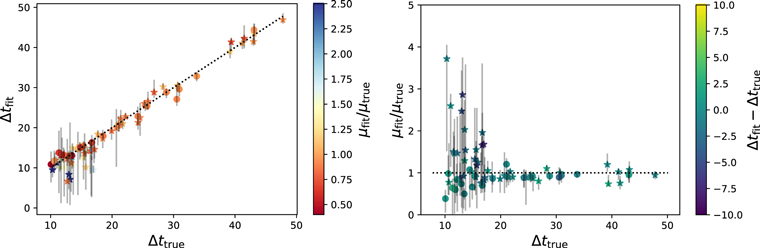
Figure 12 shows the results for the time delays and magnifications. The method holds, though on this set it gives a larger fraction of systems not accepted as having confident detection of unresolved lensing (Δtfit < 10 days).
Figure 12. Same as Figure 9, but for the noisier validation set consisting of 71 ZTF-like systems from Goldstein et al. (2019). Both panels again show fits matching the true values. Uncertainties are somewhat larger compared to Figure 9, due to a higher overall noise level in this set.
Download figure:
Standard image High-resolution imageCombining the Goldstein sets of 33 + 71 lensed SN, Figure 13 presents histograms of scatter of the best-fit from the true values, again for the outcomes where we accept the fit results—either Δtfit > 10 or 15 days. The histograms remain well-peaked near the true values, though with increased scatter from the increased noise.
Figure 13. Same Figure 10, but for the consolidated set consisting of 33 + 71 = 104 ZTF-like systems from Goldstein et al. (2019). Note that 97 systems satisfy the condition Δtfit ≥ 10 days that corresponds to the blue histogram in either of the panels, whereas the orange histograms enclose 54 systems. Again, we find that, for most of the systems, our fit estimations are close to the respective true values.
Download figure:
Standard image High-resolution image4.6. Assessing Precision and Accuracy
An important aspect of the use of lensed SN for cosmology is quantifying the fit precision and accuracy. We assess these below for the unresolved lensed SN we have studied.
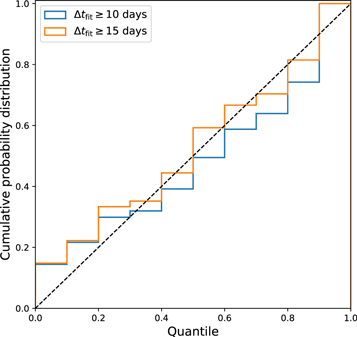
For the fit precision, i.e., the uncertainty on the estimation, we investigate the cumulative pull distribution from the sampling chains, shown in Figure 14. By examining the amount of probability between the 16% and 84% quantiles, we find that the chains are underestimating the Δtfit uncertainties by approximately a factor of 0.71 for the systems with Δtfit ≥ 10 (and 0.87 for Δtfit ≥ 15 days). This is not uncommon for flexible model spaces where the full parameter space is not thoroughly sampled. Indeed, as mentioned in Section 3.2.2, some of the priors on the nonphysical hyperparameters are informative, e.g., running into the boundary (and extending the boundary lowers the code efficiency and convergence). Thus, the details of the derived PDFs, including potentially for the time delays and magnifications, can be affected. However, this does not seem to be the case for the best-fit values, as seen in the accuracy tests below. Methods for improving uncertainty quantification are being developed in further work, but we will not use the uncertainties quantitatively in this article. We can, however, still assess the accuracy of the method for the best fits.
Figure 14. Cumulative probability distribution from the consolidated set consisting of 33 + 71 = 104 ZTF-like systems from Goldstein et al. (2019). Histograms basically show the fraction of the systems for which the true time delay falls within a given probability quantile of the fit distribution. Significant deviations from the diagonal dashed line indicate under- or overestimation of the uncertainty. The amount of probability between the 16% and 84% percentiles is found to be 48.5% for the systems with Δtfit ≥ 10 days (blue curve), and 59.3% for the systems with Δtfit ≥ 15 days (orange curve). Therefore, we find that the uncertainty in the estimated time delay, σ(Δtfit), is underestimated by a factor of about 0.71 for the blue curve and 0.87 for the orange curve. This can be due in part to insufficient statistics, e.g., having only 97 (54) systems in the blue (orange) histogram.
Download figure:
Standard image High-resolution imageWith regard to the fit accuracy, we want to ensure it in two respects. The first is a low fraction of false positives: cases that are fit as unresolved lensed SN even though in reality they are single unlensed images. The second is bias in the time delay measurement: are estimates statistically scattered about the truth or are they systematically offset low or high?
The false-positive rate was estimated by running 360 unlensed SNe in Section 4.2 in addition to the 12 in Section 4.1, as well as including unlensed SNe in the blind data set in Section 4.3 and considering what fraction of their fits have spurious time delay measurements inconsistent with zero delay. From the results in those subsections, the fraction of false positives can be estimated as ≲5% (19 out of 381), mostly due to the higher noise levels, if we use Δtfit > 10 days, but 0 out of 381 for Δtfit > 12 days.
The second type of accuracy is bias. To assess bias, we compare the ensemble of fit time delays to the true inputs through (Hojjati & Linder 2014; Liao et al. 2015)

Note that this uses the best fit and does not involve the fit uncertainty. Fits that scatter positive and negative about the truth for the time delay do not bias cosmology estimation; only a systematic offset relative to truth shifts the cosmology. 7
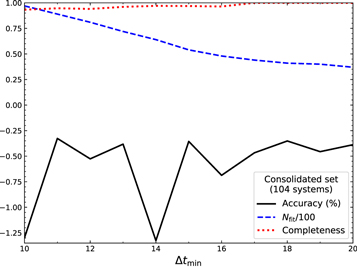
Figure 15 shows the accuracy as a function of which fits we accept. Nominally, from previous sections, we have confidence in results with Δtfit ≥ 10 days, i.e., 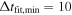 days. We study the results as a function of
days. We study the results as a function of 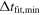 , finding that, as soon as we move away from the boundary of 10 days, where slight variations in fit can cause the best fit to move above or below
, finding that, as soon as we move away from the boundary of 10 days, where slight variations in fit can cause the best fit to move above or below 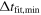 despite much of the probability distribution remaining below, the accuracy ranges mostly over the 0.3%–0.5% level. For cosmology use with a rather advanced data set with small statistical uncertainty, Hojjati & Linder (2014) derived a 0.2% accuracy requirement—that was for lens systems giving 1% distance measurements in each of six lens redshift bins from zlens = 0.1–0.6 (see also Aghamousa & Shafieloo 2015, 2017). Since that is rather ambitious for unresolved lensed SNe alone, we regard ∼0.5% accuracy as quite good enough to start.
despite much of the probability distribution remaining below, the accuracy ranges mostly over the 0.3%–0.5% level. For cosmology use with a rather advanced data set with small statistical uncertainty, Hojjati & Linder (2014) derived a 0.2% accuracy requirement—that was for lens systems giving 1% distance measurements in each of six lens redshift bins from zlens = 0.1–0.6 (see also Aghamousa & Shafieloo 2015, 2017). Since that is rather ambitious for unresolved lensed SNe alone, we regard ∼0.5% accuracy as quite good enough to start.
Figure 15. Accuracy A, Equation (5), important for using time delays as a robust cosmological probe, is plotted vs. 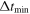 , where only systems with
, where only systems with 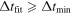 are accepted as unresolved lensed SN. The accuracy mostly lies around 0.3%–0.5%. For limited numbers of systems in the sample, deviations in one or two systems can impact the accuracy; the number of accepted systems is shown by the dashed blue curve Nfit/100. Completeness, i.e., the fraction of systems that should have been accepted, given a perfect fit, and were accepted as robust unresolved lens SN, is shown by the dotted red curve.
are accepted as unresolved lensed SN. The accuracy mostly lies around 0.3%–0.5%. For limited numbers of systems in the sample, deviations in one or two systems can impact the accuracy; the number of accepted systems is shown by the dashed blue curve Nfit/100. Completeness, i.e., the fraction of systems that should have been accepted, given a perfect fit, and were accepted as robust unresolved lens SN, is shown by the dotted red curve.
Download figure:
Standard image High-resolution imageOne might also consider false negatives, where the fit considers multiple images as one unlensed source. We will mostly address this in future work where we fit for the number of images, e.g., does the algorithm accurately identify the number of components? Here, we simply mention that, for systems with true time delays more than ten days, there are zero cases where the time delay fit is consistent with zero delay, i.e., no lensing. We can also quantify the completeness, i.e., for how many systems we have sufficient confidence in the fit to include them in the results. We quantify this by taking the total number with 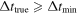 and asking for how many of these we obtained any fit (i.e., Δtfit > 10 days). The completeness is shown as the dotted red curve in Figure 15: it ranges from 93% at
and asking for how many of these we obtained any fit (i.e., Δtfit > 10 days). The completeness is shown as the dotted red curve in Figure 15: it ranges from 93% at 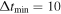 days to 97% at
days to 97% at 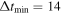 days and 100% at
days and 100% at 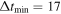 days.
days.
5. Conclusions
Strong gravitational lensing allows us to see a source in different positions and at different times, and so can serve as an important cosmological probe. Lensed SN possess advantages over lensed quasars, in that they have a better understood intrinsic lightcurve with a characteristic timescale on the order of a month, allowing time delay estimation after months rather than many years of monitoring. Surveys currently underway, such as ZTF, and forthcoming ones, such as ZTF-2 and LSST, will greatly increase the number of lensed SN detected. However, if the time delay is on the order of or shorter than the characteristic SN timescale, i.e., about a month, then the lensed nature may not be obvious either from the observed lightcurve (a superposition of the image lightcurves) or spatially resolved on the sky.
Here, we investigate these unresolved lensed SN, and we put forward a method for robustly extracting the time delays (and image magnifications). For this first step, we consider Type Ia systems with two images only, without microlensing. The time delays are directly related to the time delay distance of the supernova, adding a highly complementary cosmological probe to standard luminosity distance measurements. Knowledge of the magnifications provides important constraints on the lens modeling, which are needed as well. Once a transient is identified as a lensed supernova, additional resources such as high-resolution imaging from ground-based adaptive optics systems or space-based telescopes can target it to resolve images spatially.
Our method, involving an orthogonal basis expansion around a trial lightcurve, sampled over many parameters for each band and image through Hamiltonian Monte Carlo, shows great promise. In this article, we thoroughly test the method on lensed SN Ia systems with sampling cadence and noise levels representative of ZTF and LSST surveys (without considering the microlensing effects for simplicity). We recover the time delays (and magnifications) accurately down to Δtfit ≳ 10 days. The false-positive rate (interpreting an unlensed SN as a lensed one) is below 5%, and the completeness (finding actually lensed SN as lensed) is 93% or better. Time delay measurement can accurately control bias to ∼ 0.5%. We emphasize that these numbers apply to the Type Ia systems we have tested; we have not yet assessed other SN or transient types.
Nevertheless, the fundamentals of this technique are broadly applicable and do not rely fundamentally on SN properties. The method can be used for any transient lightcurve, with proper adjustment of hyperparameter priors (although we have not yet tried doing so). Hamiltonian Monte Carlo provides a potentially robust sampling technique for the multidimensional parameter space necessary; our particular cases allowed 24 parameters, but there is no innate limit.
Significant further developments can be made. Our future work will include fitting for the number of images as part of the process (here, we did only one versus two, i.e., unlensed versus two lensed images, but four-image systems tend to have better constrained lens mass models, which is an important consideration), increasing flexibility in the template plus basis expansion approach, accounting for microlensing, and establishing cadence, noise, or other requirements to push the minimum time delay for which we have confidence in the results into the regime Δtfit < 10 days. Of course, we also greatly look forward to applying the method to real data from surveys and discovering a significant sample of unlensed SN.
S.B. thanks Ayan Mitra, Tousik Samui, and Shabbir Shaikh for their helps at different stages of the project. A.K. and E.L. thank the Cosmology Group at KASI for hospitality during the early part of this work. A.K. and E.L. are supported in part by the U.S. Department of Energy, Office of Science, Office of High Energy Physics, under contract no. DE-AC02-05CH11231. E.L. is also supported under DOE Award DE-SC-0007867 and by the Energetic Cosmos Laboratory. A.S. would like to acknowledge the support of the Korea Institute for Advanced Study (KIAS) grant funded by the government of Korea.
Appendix A: Hyperparameter and Time Delay Priors
The priors on the intrinsic lightcurve parameters, i.e., the hyperparameters, are presented in Table 1. In this appendix, we give some more detail. We again caution that priors tend to involve the astrophysics of the source, and their specific values need to be adjusted depending on the type of transient. Here, we focus on normal SNe Ia. Apart from the specific priors, however, the method described in the main text should be broadly applicable to many unresolved lensed transients.
The parameter bj (known as the scale parameter in lognormal distributions) is a logarithmic time variable that gives the median of the distribution. Because an SN falls more slowly than it rises, and it peaks about 20 days after explosion, the median is around 30 days. This translates to bj ≈ 3.4. Less than 20 days or longer than 60 days (e.g., for the longer-wavelength bands) seem not to be useful parts of the parameter space, so we adopt bj ∈ [3.0, 4.1]. In the fits to the data, we find bj ≈ 3.4, and none of the fits closely approach the prior bounds.
The parameter σj
(known as the shape parameter) relates to the (logarithmic) width of the distribution and interacts with bj
to give skewness, shifting the mode (and mean) from the median. In particular, the mode, i.e., maximum flux, occurs at 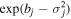 . If the median is 30 days and the mode is at 20 days after explosion, then σj
≈ 0.64. Extending the maximum all the way to 30 days after explosion would still give σj
< 0.8 for the largest bj
, i.e., the latest median. For the maximum no earlier than 17 days after explosion, one gets σj
> 0.4 for the smallest bj
. Thus, the range adopted is σj
∈ [0.4, 0.8]. In the fits to the data, we find μ ≈ 0.64, and none of the fits closely approach the prior bounds.
. If the median is 30 days and the mode is at 20 days after explosion, then σj
≈ 0.64. Extending the maximum all the way to 30 days after explosion would still give σj
< 0.8 for the largest bj
, i.e., the latest median. For the maximum no earlier than 17 days after explosion, one gets σj
> 0.4 for the smallest bj
. Thus, the range adopted is σj
∈ [0.4, 0.8]. In the fits to the data, we find μ ≈ 0.64, and none of the fits closely approach the prior bounds.
Note that these priors are specific to normal SNe Ia we would use for cosmology. They are motivated by the lognormal template, which will be further modified by the basis expansion terms. However, they work well in practice. For other supernovae, or other transients, the priors would need to be adjusted, although the fitting method should still be substantially unchanged.
The fit shift parameter t1 comes from numerics using noisy data, not the astrophysics of supernovae. For low flux, photon noise and photometry scatter are especially influential, and the explosion time can be misestimated. Introducing t1 helps mitigate this, as the fit can be shifted to be optimized by taking into account the full run of data. Numerical experimentation shows that t1 ∈ [ − 5, 5] days provides a reasonable estimation, though this parameter is less well-constrained.
For the normalization prior Nj , this is a convolution of the intrinsic lightcurve amplitude, the scaling adjustment by the basis function multiplication (essentially C0,j ), and the (not directly observed) magnification of the first image. Therefore, it is a combination of supernova and lensing properties, and one should also keep in mind numerical efficiency. This can become complicated, but in brief, we set priors on Nj depending on the single/double-peak nature of the observed lightcurve, taking into account the observed maximum flux and the physically reasonable range of magnifications. See Appendix B for further details.
The time delay fit parameter itself has a prior as well, as we described in Section 3.2.1. Here, we go into additional detail. In the event of a single flux peak, if its width (full width at 80% peak height, w80) is more than 20 days, we shift the prior on Δt. Taking δ t = (w80 − 20)/1.8, the prior on Δt becomes δ t ≤ Δt ≤ 30 + δ t. In addition, since the relative magnification cannot be very small in these cases, we impose a lower limit on μ, leading to the prior 0.25 ≤ μ ≤ 4. In the two-peak case, there is no need for adjustment of the priors. Again, these priors are specific to normal SNe Ia and should be adjusted for other transients.
Appendix B: Prior on the Normalization Parameter
Separation of the basis expansion factor C0,j within the normalization factor Nj in Equation (3) can improve convergence in the sampling. We write
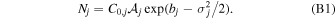
The exponential term ensures that the flux function in Equation (3) without shape modifications from the basis expansion terms,
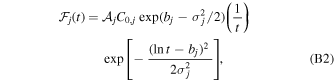
has a maximum height 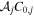 , independent of bj
, σj
. Now C0,j
is used as the fit parameter. The amplitude
, independent of bj
, σj
. Now C0,j
is used as the fit parameter. The amplitude 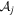 is determined from the observed data as a fraction of the maxima of the observed summed lightcurve,
is determined from the observed data as a fraction of the maxima of the observed summed lightcurve,
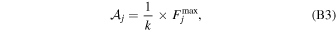
where the constant k can be any number greater than unity.
Now suppose the true (unobserved) maxima of the lightcurves of the first and the second image are Bj1 and Bj2, respectively, in the jth filter. If we set C0,j
such that 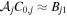 , then the desired value of C0,j
would be
, then the desired value of C0,j
would be
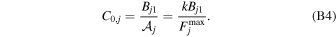
We have two inequalities between Bj1, Bj2, and 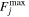 :
:
- 1.
 , which yields C0,j
≤ k.
, which yields C0,j
≤ k. - 2.
 , which yields C0,j
≥ k/(1 + μ), given that the true magnification is μ = Bj2/Bj1.
, which yields C0,j
≥ k/(1 + μ), given that the true magnification is μ = Bj2/Bj1.
Therefore, a useful prior on C0,j is
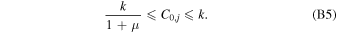
Taking a wide prior on μ as 0 ≤ μ ≤ 4, and setting k = 2 (as if the two images contribute equally, i.e., not favoring either), the prior on C0,j becomes
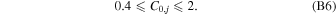
This is what we list in Table 1 and use in the text.
Footnotes
- 6
Supernovae are observed in modified Julian days (MJD). We subtract the time of the start of the observation in MJD from all the observation times. The quantity
 is the time we end the fit in band j (e.g., due to lack of data or fading of the supernova). Note that a nonzero t1 in Equation (1) simply shifts the lightcurves earlier or later in time; we actually consider t1 as a free parameter (same for all the filters) in order to allow the fit to the observed lightcurve data to begin a little before or after the nominal explosion time, to account for random scatter in the data near zero flux, so t → t − t1 in Equation (2).
is the time we end the fit in band j (e.g., due to lack of data or fading of the supernova). Note that a nonzero t1 in Equation (1) simply shifts the lightcurves earlier or later in time; we actually consider t1 as a free parameter (same for all the filters) in order to allow the fit to the observed lightcurve data to begin a little before or after the nominal explosion time, to account for random scatter in the data near zero flux, so t → t − t1 in Equation (2). - 7
This holds for time delay distance; parameters related nonlinearly, such as the Hubble constant, can still be biased, as high fluctuations do not perfectly balance low fluctuations if the scatter is not small, as for any probe.