ABSTRACT
It is well established that Mg ii absorption lines detected in background quasar spectra arise from gas structures associated with foreground galaxies. The degree to which galaxy evolution is driven by the gas cycling through halos is highly uncertain because their gas mass density is poorly constrained. Fitting the Mg ii equivalent width (W) distribution with a Schechter function and applying the N(H i)–W correlation of Ménard & Chelouche, we computed Ω(H i)Mg ii ≡ Ω(H i)halo = 1.41+0.75−0.44 × 10−4 for 0.4 ⩽ z ⩽ 1.4. We exclude damped Lyα's (DLAs) from our calculations so that Ω(H i)halo comprises accreting and/or outflowing halo gas not locked up in cold neutral clouds. We deduce that the cosmic H i gas mass density fraction in galactic halos traced by Mg ii absorption is Ω(H i)halo/Ω(H i)DLA ≃ 15% and Ω(H i)halo/Ωb ≃ 0.3%. Citing several lines of evidence, we propose that infall/accretion material is sampled by small W whereas outflow/winds are sampled by large W, and find that Ω(H i)infall is consistent with Ω(H i)outflow for bifurcation at W = 1.23+0.15− 0.28 Å; cold accretion would then comprise no more than ∼7% of the total H i mass density. We discuss evidence that (1) the total H i mass cycling through halos remains fairly constant with cosmic time and that the accretion of H i gas sustains galaxy winds, and (2) evolution in the cosmic star formation rate depends primarily on the rate at which cool H i gas cycles through halos.
1. INTRODUCTION
Our knowledge of galaxy evolution relies heavily on both observations and simulations that focus on the mechanisms by which galaxies acquire, chemically enrich, recycle, and expel their gaseous component. However, the mean quantity of halo gas engaged in any given process remains poorly constrained. The use of quasar absorption lines provides a unique tool to directly observe these ongoing processes and allows for sensitive measures of the quantity of gas within galaxy halos along with their cross sections, kinematics, metallicities, densities, and temperatures.
The dense neutral hydrogen that is mostly confined within galaxies commonly exhibits damped Lyα (DLA) absorption (N(H i) ⩾ 2 × 1020 cm−2). DLAs are fundamentally different from other classes of absorption systems. For example, the Lyman limit systems (LLSs; 1017.3 cm−2 < N(H i) < 1020.3 cm−2) have varying degrees of hydrogen ionization (cf. Prochaska 1999) and extend out to ∼100 kpc around galaxies,5 whereas DLAs are believed to probe the cool, dense precursors of star-forming molecular clouds and can account for up to ∼50% of the galactic baryonic content (cf. Wolfe et al. 2005).
In an effort to determine the quantity of dense gas within galaxies, Rao et al. (2006) measured the cosmological neutral gas mass density traced by DLAs to be Ω(H i)DLA = (9.6 ± 4.5) × 10−4 at 〈z〉 = 0.92. It has also been argued that Ω(H i)DLA remains roughly constant for z ∼ 0.2–5 (Prochaska & Herbert-Fort 2004; Péroux et al. 2005; Rao et al. 2006; Lah et al. 2008; Songaila & Cowie 2010; Meiring et al. 2011) and then decreases by a factor of ∼2–3 by z = 0 (Zwaan et al. 2005a; Martin et al. 2010). There is also some evidence showing that Ω(H i)DLA might decrease below z = 2.2 (Noterdaeme et al. 2009).
The global star formation rate (SFR) history of the universe has evolved dramatically (e.g., Bouwens et al. 2011) and if the redshift constancy of Ω(H i)DLA holds, then this implies that DLA gas does not directly track the formation of stars. This might imply that the global SFR is predominantly governed by mechanisms linked to galactic halos, such as gas accretion from the intergalactic medium and/or recycling of gas within the galaxy halos. An estimate of Ω(H i)halo (excluding H i from DLAs), being the sum of an accreting/infall component (Ω(H i)infall) and a wind/outflow component (Ω(H i)outflow), could place constraints on the relative importance and roles with which these processes drive star formation in galaxies.
The Mg ii λλ2796, 2803 absorption doublet, which probes low-ionization gas with 1016 cm-2 ⩽ N(H i) ⩽ 1022 cm−2, is commonly used to study the gaseous components of galaxies (see Churchill et al. 2005, for a review). The Mg ii absorption is observed out to projected galactic radii of ∼100 kpc (Kacprzak et al. 2008; Chen et al. 2010a).
For Mg ii absorption systems with rest-frame equivalent widths of W ⩾ 1 Å, galaxy color and SFR correlate strongly with W (Zibetti et al. 2007; Noterdaeme et al. 2010; Nestor et al. 2011), a result highly suggestive of the fact that galactic outflows are responsible for ejecting substantial amounts of gas to large galactocentric radii. The outflow scenario is also supported by the result of Bouché et al. (2006), who found an anti-correlation between W and the host halo mass, by cross-correlating Mg ii absorbers with luminous red galaxies from SDSS, and claim that this provides evidence that absorbers are not virialized in gaseous halos of the galaxies. They suggest that the strong absorbers are statistically more likely to trace super-winds.
Indeed, direct evidence for Mg ii absorbing winds is seen in spectra of star-forming galaxies, which exhibit strong outflows blueshifted 300–1000 km s−1 relative to the galaxy (Tremonti et al. 2007; Weiner et al. 2009; Martin & Bouché 2009; Rubin et al. 2010b). These galaxies almost exclusively exhibit W ⩾ 1 Å absorption. Chelouche & Bowen (2010) demonstrated that models of outflowing wind-driven gas reproduce the Mg ii velocity widths of W ⩾ 1 Å systems observed with high resolution. The extent of these Mg ii absorbing winds are not well constrained; however, Bordoloi et al. (2011) suggest that they may reach out to ∼50 kpc.
For samples dominated by W < 1 Å, neither Chen et al. (2010a) nor Kacprzak et al. (2011b) found a W–galaxy color correlation, contrary to the Zibetti et al. (2007) result for W > 1 Å. Furthermore, Chen et al. (2010b) found that Mg ii “halo size” increases with increasing galaxy stellar mass and weakly with specific SFR, suggesting a scenario in which infalling Mg ii absorbing gas structures (selected by W < 1 Å absorption) fuel star formation.
The smoothed particle hydrodynamic simulations of Stewart et al. (2011a) reveal that gas-rich mergers and cold-flow streams produce a circumgalactic corotating, low-ionization gas component that is predominately infalling toward the galaxy. In absorption, these structures are expected to exhibit ∼100 km s−1 velocity offsets relative to the host galaxy, consistent with the observations of Steidel et al. (2002), Kacprzak et al. (2010), and Kacprzak et al. (2011a). This spatial/kinematic configuration yields a correlation between galaxy inclination and W, which has been previously observed by Kacprzak et al. (2011b).
The above body of evidence suggests that weaker Mg ii absorption selects gas accretion from infalling cold streams or cooled gas returning from earlier processing within the galaxy, whereas stronger absorption (W ⩾ 1 Å) selects outflows. It would be useful to constrain the relative neutral gas mass density for both processes, i.e., Ω(H i)halo = Ω(H i)infall + Ω(H i)outflow, to gain insight into how much galactic gas is cycled through either mechanism at a given time and how this compares to Ω(H i)DLA.
In this Letter, we compute the H i mass density within galaxy halos traced by Mg ii absorption, Ω(H i)halo ≡ Ω(H i)Mg ii. We apply the N(H i)–W relation of Ménard & Chelouche (2009) to obtain the H i column density distribution function directly from the Mg ii equivalent width distribution function. We exclude DLAs from our calculations so that Ω(H i)halo budgets gas likely to be accreting and/or outflowing from galaxies but not locked up in cold neutral clouds. We apply a 1 Å bifurcation to compute Ω(H i)infall and Ω(H i)outflow, and determine W at which Ω(H i)infall = Ω(H i)outflow. Throughout this letter we adopt an h = 0.70, ΩM = 0.3, and ΩΛ = 0.7 cosmology.
2. COMPUTING Ω(H i) FROM Mg ii
The cosmological neutral hydrogen gas mass density is computed from
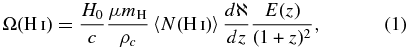
given that
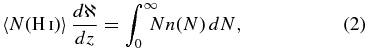
where n(N) is the H i column density distribution function, μ = 1.3 is the mean molecular weight,6 ρc is the critical density of the universe, H0 is the Hubble constant, mH is the mass of hydrogen, <N(H i)> is the mean H i column density, dℵ/dz is the number of systems per unit redshift, and E(z) = H(z)/H0 = [ΩM(1 + z)3 + ΩΛ]1/2.
Computing Ω(H i) traced by Mg ii absorption requires n(N), which is not directly observationally known for Mg ii absorbers. However, Ménard & Chelouche (2009) determined the geometric mean column density as a function of W to be N(H i) = AWβ, where A = (3.06 ± 0.55) × 1019 cm−2 Å−β and β = 1.73 ± 0.26 for 0.5 Å ⩽W ⩽ 3 Å and 0.5 ⩽ z ⩽ 1.4. Employing this column density relation, we can obtain n(N)dN from the equivalent width distribution, n(W)dW, where n(W) is the distribution of Mg ii rest-frame equivalent widths.
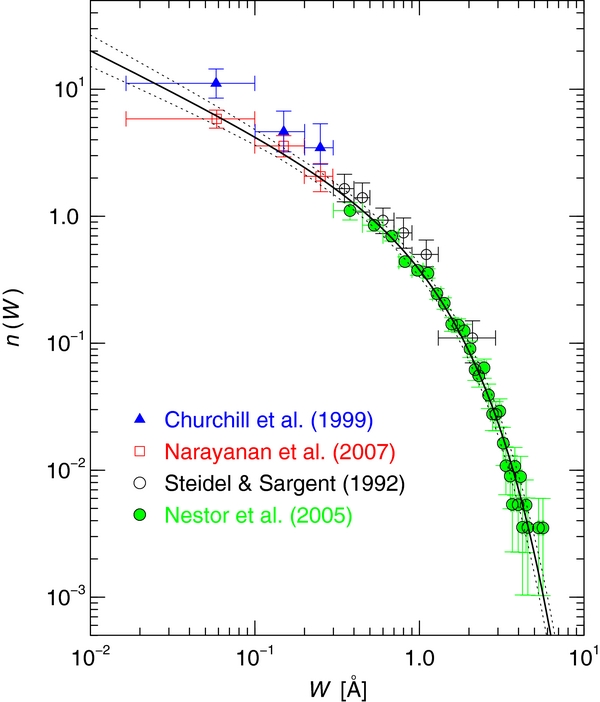
In Figure 1, we plot n(W) versus W using the data of Steidel & Sargent (1992), Churchill et al. (1999), Nestor et al. (2005), and Narayanan et al. (2007). Since the work of Steidel & Sargent (1992), it has been common to fit n(W) as either a power law or an exponential function. For W ⩾ 0.3 Å, Steidel & Sargent (1992) could not distinguish which function was preferred, whereas Nestor et al. (2005) showed that the distribution was clearly exponential. For W ⩽ 0.3 Å, Churchill et al. (1999) showed that n(W) is a power law that is consistent with the Steidel & Sargent (1992) data for W ⩽ 1.0 Å, which was confirmed by Narayanan et al. (2007).
Figure 1. Distribution of Mg ii rest-frame equivalent widths, n(W), using the data from Churchill et al. (1999; blue triangles), Narayanan et al. (2007; red open squares), Steidel & Sargent (1992; black open circles), and Nestor et al. (2005; green circles). We fitted the data using a Schechter function (solid curve) with parameters C* = 1.08 ± 0.12 Å−1, α = −0.642 ± 0.062, and W* = 0.970 ± 0.056 Å. The dashed curves represent the maximum 1σ error in the fit for the parameter uncertainties.
Download figure:
Standard image High-resolution imageWe used χ-squared minimization to fit a Schechter (1976) function to the binned data,
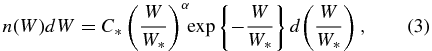
where C* is the normalization such that the unweighted integral is equal to dℵ/dz (to satisfy Equation (2)). In Figure 1, we show our fit with parameters C* = 1.08 ± 0.12 Å−1, α = −0.642 ± 0.062, and W* = 0.970 ± 0.056 Å. The overall equivalent width distribution at <z > =1.0 is a much better fit with a Schechter function than the power law only (see Figure 6 of Narayanan et al. 2007) or with the exponential only (see Figure 20 of Nestor et al. 2005). Interestingly, the characteristic equivalent width, W*, marking the transition from a power law to an exponential distribution, is consistent with 1 Å. Based upon the results discussed in Section 1, we speculate the break in the n(W) distribution at W ≃ 1 Å is physical, and that infall/accretion structures yield a power-law distribution whereas outflowing/wind structures yield an exponential distribution.
We note there are subtle differences between the data sets shown in Figure 1. The W < 0.3 Å data of Churchill et al. (1999; 30 systems) and Narayanan et al. (2007; 112 systems) represent 0.4 ⩽ z ⩽ 1.4 and have mean redshift of <z > =0.9. The W ⩾ 0.3 Å data of Steidel & Sargent (1992; 103 systems) represent 0.2 ⩽ z ⩽ 2.2 with <z > =1.1, and the data of Nestor et al. (2005; 1331 systems) represent 0.4 ⩽ z ⩽ 2.3, also with <z > =1.1. Thus, the redshift ranges of the low and high equivalent width samples are not identical, even though the <z > are fairly consistent. Both Steidel & Sargent (1992) and Nestor et al. (2005) demonstrated redshift evolution of n(W) in that there is more power at large W at higher redshifts. This evolution is expected to result in a slightly larger W* than if we confined their samples to z ⩽ 1.4 (the upper limit of the W < 0.3 Å data). Given that the mean redshifts of both of the W ⩾ 0.3 Å samples, <z > = 1.1, are similar to those of the W < 0.3 Å samples, <z > = 0.9, we expect that this slightly increased power in n(W) has only a minor influence on our final Ω (H i)halo result as compared to, for example, the uncertainty in the fitted values of A and β in the column density relation of Ménard & Chelouche (2009). We also note (see Figure 1) a slight vertical offset between the two W < 0.3 Å data sets and between the two W ⩾ 0.3 Å data sets. In both cases the larger surveys yield slightly smaller dℵ/dz and the source of the offsets is still unknown.
We now substitute N(H i) = AWβ into Equations (1)–(3) and derive
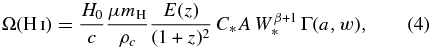
where Γ(a, w) is the incomplete gamma function with a = α + β + 1. The value of w allows integration over specific W intervals: w = Wmax/W* for integration 0 → w, and w = 0 or Wmin/W* for integration w → ∞, where Wmin and Wmax are selected cutoffs.
To compute Equation (4), we are required to extrapolate the column density relation of Ménard & Chelouche (2009) to W values both lower and higher than the domain of their fit. Though there is scatter in the column density relation, it correctly predicts that W < 0.3 Å absorption systems are sub-LLSs with log N(H i) < 17, consistent with the observations of Churchill et al. (2000).
Since we desire to compute the H i mass density in galaxy halos, we correct for the quantity of H i found in disks. The majority of DLAs lie within the optical disk and exhibit covering fractions of virtually 100% (e.g., Zwaan et al. 2005b), thus correcting for the H i DLA absorption provides a good approximation for the disk contribution of H i. Though some DLAs may arise in halos, this fraction is estimated to be less than 1%–5% (Fumagalli et al. 2011).
Rao et al. (2006) showed that the probability of a Mg ii selected DLA system is P(W) = 0 for W < 0.6 Å and then increases with increasing W for W ⩾ 0.6 Å. Using a maximum-likelihood fit to the binned data in their Figure 4, we estimate this increase as a linear function P(W) = 0.23W − 0.057 for 0.6 ⩽ W ⩽ 4.5 Å with P(W) = 1 for W > 4.5 Å. In order to correct for DLA contamination in our calculation, we weight Equation (4) by P(W) − 1. The upper limit of W = 4.5 Å, where DLA contamination is 100%, is consistent with the Ménard & Chelouche (2009) column density relation, which predicts log N(H i)>20.3 for W ⩾ 4.5 Å.
3. RESULTS AND DISCUSSION
In Table 1, we present Ω(H i) for selected W ranges. The quoted uncertainties are the 1σ confidence levels based upon the uncertainties in the fitted parameters C*, α, W*, A, and β. We deduce the H i mass density traced by Mg ii absorption, which is interpreted as the diffuse H i contained within galaxy halos, is Ω(H i)halo = 1.41+0.75−0.44 × 10−4. This value is ∼15% of Ω(H i)DLA, indicating that a considerable fraction of H i is contained in galaxy halos relative to the H i in DLAs; it contributes 0.3% to the total baryonic budget (Ωb = 0.045; Jarosik et al. 2011) at <z > =1.0.
Table 1. Ω(H i) Traced by Mg ii at 0.4 ⩽ z ⩽ 1.4
| Ω(H i) | Ω(H i)/Ω(H i)DLA | W range | |
|---|---|---|---|
| (Å) | |||
| Ω(H i)halo | 1.41+0.75− 0.44 × 10−4 | 0.147 | 0.0–∞a |
| Ω(H i)infall | 5.56+2.60− 1.54 × 10−5 | 0.058 | 0.0–1.0 |
| Ω(H i)outflow | 8.57+0.86− 1.10 × 10−5 | 0.089 | 1.0–∞a |
| Ω(H i)(<0.3)Mg ii | 7.71+8.71− 3.88 × 10−6 | 0.008 | 0.0–0.3 |
Note. aFor W > 4.5 Å, DLA contamination is 100% and the contribution to Ω(H i)halo vanishes. See the text for further discussions.
Download table as: ASCIITypeset image
We find that W ⩽ 0.3 Å Mg ii absorption (often called “weak” systems, e.g., Churchill et al. 1999) selects a small fraction of the H i mass density, Ω(H i)(<0.3)Mg ii = 7.71+8.71−3.88 × 10−6. From this quantity, it is difficult to ascertain what fraction of these systems could be selecting Lyα forest structures versus galactic halo structures because estimates of ΩLyα in the appropriate N(H i) range (1015.5–1016.5 cm−2) are highly uncertain and are quoted in units of total gas mass density (neutral + ionized; cf. Penton et al. 2004). The simulations of Davé et al. (2010) indicate that Ω(H i) ≃ 10−7 for N(H i) ⩽ 1015 (outside halos) at z ∼ 0.1, where the H i fraction in the Lyα forest is at its highest.
We previously described the theoretical and observational evidence supporting the idea that weaker Mg ii systems trace infall/accretion and stronger systems trace outflow/winds and that W* ≃ 1 Å marks the transition between the two regimes. Applying a 1 Å bifurcation to Ω(H i)halo, we find Ω(H i)infall = 5.56+2.60−1.54 × 10−5 and Ω(H i)outflow = 8.57+0.86−1.10 × 10−5. The former is 6% of ΩDLA and 0.1% of Ωb, and latter is 9% of ΩDLA and 0.2% of Ωb. The range of W over which the infall and outflow Ω(H i) are statistically consistent is W = 1.23+0.15− 0.28 Å.
There is no a priori expectation that our approach to computing Ω(H i)halo should yield Ω(H i)infall ≃ Ω(H i)outflow for W ≃ W*. Our result may indicate that, over a redshift range covering a large percentage of the age of the universe in the “post-star-forming era,” a cyclic balance persists between inflow and outflow of galaxies whereby star formation is fueled by accreting gas and then an equal mass of gas is ejected back into the halos. This is quite suggestive of a halo gas recycling model (e.g., Oppenheimer & Davé 2008).
Noterdaeme et al. (2009) extrapolated their H i column density distribution below log N(H i) = 20.3 and found that LLSs contribute ≃13% of the total Ω(H i) at z > 2.2 (also see Péroux et al. 2005). If we assume Ω(H i)tot = Ω(H i)halo + Ω(H i)DLA, we obtain Ω(H i)halo ≃ 13% of Ω(H i)tot for 0.4 ⩽ z ⩽ 1.4; since Ω(H i)DLA is constant with redshift, this suggests that Ω(H i)halo has remained constant with redshift and implies that the H i mass cycling through halos via infall/outflow has also remained constant.
Thus, given the cosmic evolution of the global SFR (especially below z ≃ 2), and presuming galactic infall/outflow is strongly coupled to star formation, the global SFR must be governed by the rate at which H i gas cycles through halos (i.e., the SFR and H i halo cycling rate must evolve in parallel). The observation that the mean ionization of Mg ii absorbers has decreased with decreasing redshift from z ∼ 2 (Bergeron et al. 1994) is consistent with this scenario. At higher redshift, the more highly ionized H i halo gas selected by Mg ii absorption constitutes a smaller fraction of the total gas associated with H i; at lower redshift, the more neutral H i gas constitutes a larger fraction of the total gas mass. Thus, the total gas mass associated with H i that is cycling through halos is higher at high redshift and lower at low redshift for a fixed H i mass. Based upon simulations, it is predicted that the total halo gas mass increases with decreasing redshift to the present epoch (e.g., Davé et al. 1999), however, this is not inconsistent with our proposed scenario because this growth is in the “hot” phase that is neither detected via Mg ii absorption nor a reservoir for star formation.
Ribaudo et al. (2011) presented possible observational evidence of cold accretion in a [Mg/H] = -1.7 LLS at z = 0.27 near a Z ≃ Z☉ sub-L* galaxy. Cosmological simulations predict that cold accretion is truncated at low redshifts (e.g., Fumagalli et al. 2011; Stewart et al. 2011b) such that the cross section of this gas is a tiny fraction of the observed Mg ii cross section (Kacprzak et al. 2008; Chen et al. 2010a). If cold, metal-poor filaments comprise a component of the infalling material, our findings imply they constitute no more than ∼7% of Ω(H i)tot at <z > =1.0.
Our calculation of Ω(H i)halo relies heavily on the statistical N(H i)–W relation of Ménard & Chelouche (2009), which we extrapolated to W = 0 and W = 4.5 Å. For our calculations of Ω(H i)infall and Ω(H i)outflow, we assumed the break in the n(W) Schechter function at W* ≃ 1 Å is due to infall/accretion for W < W* and outflowing/winds for W > W*. A bifurcation at ≃ 1 Å in the equivalent width distribution separating the two physical processes of infall and outflow is an intriguing result that is not well understood within the framework of current models. In reality, some fraction of the W < 1 Å absorbers could arise in winds and some fraction of the W > 1 Å absorbers could arise in infalling/accreting material. Nonetheless, the observational data suggest that the majority of W > 1 Å are of wind origin and vice versa. Since there are no data to constrain the possible fractional contribution of infall or outflow that may reside on either side of W*, we make no attempt to quantitatively estimate it.
Further observations are required to ascertain the veracity of this simple scenario. For example, there is mounting evidence that galaxy orientation plays some role in determining W and its origin (Kacprzak et al. 2011b; Bordoloi et al. 2011), although the evidence provided by Kacprzak et al. (2011b) supports the idea that W ≲ 1 Å systems trace accreting halo gas.
4. CONCLUSION
We have shown that the Mg ii equivalent width distribution, n(W), at <z > =1.0, is well described by a Schechter function. We combined our n(W) with the N(H i)–W relation of Ménard & Chelouche (2009) to compute Ω(H i) residing in galactic halos, as traced by Mg ii absorption (excluding DLAs). We found that 13% of Ω(H i)tot resides in galaxy halos and deduced that the infall and outflowing components comprise roughly equal H i mass contributions. The balance between the two may suggest that outflows are sustained by accretion and that cold accretion by filaments comprises less than ∼7% of Ω(H i)tot. Comparing to high-redshift results, it appears that Ω(H i)halo has not strongly evolved over cosmic time. We argued that this implies that evolution in the cosmic SFR must depend primarily on the rate at which cool H i gas cycles through halos, even through the total H i mass cycling through halos remains fairly constant.
We thank Dan Nestor for providing data in electronic form and Michael T. Murphy for carefully reading this paper. We thank the anonymous referee for providing insightful comments that improved this Letter. C.W.C. gratefully acknowledges support by Swinburne Faculty Research Grant, G.G.K., and Michael T. Murphy during his stay at the Swinburne University of Technology.
Footnotes
- 5
- 6
μ = 1.3 applies for a fully neutral gas and is the value used for DLA studies. For partially ionized gas, μ is slightly smaller, but still of order unity.